Числовые характеристики

Числовые характеристики случайного вектора состоят из числовых характеристик составляющих вектора, условных числовых характеристик и характеристик связи составляющих.

Если дискретная двумерная случайная величина () задана совместными вероятностями , то математические ожидания и дисперсии составляющих находятся по формулам:

, (41)

(42)

.

Если известны плотности вероятности составляющих двумерного непрерывного случайного вектора (), то можно найти их математические ожидание и дисперсии:

, (43)

(44)

.

Если задана совместная плотность вероятности , то следует использовать следующие формулы (двойные интегралы берутся по области возможных значений вектора):

(45)

, (46)

.

Важными характеристиками условных распределений вероятности являются условные числовые характеристики.

Условным математическим ожиданием дискретной случайной величины при называют произведение возможных значений на их условные вероятности, вычисляемые по формуле (37):

. (47)

Аналогично для случайной величины :

.

Условное математическое ожидание называют регрессией величины на .

Для непрерывных двумерных случайных величин символ суммы заменяется интегралом:

. (48)

Условной дисперсией дискретной случайной величины при называют произведение квадратов отклонений возможных значений случайной величины от их условных математических ожиданий на их условные вероятности, вычисляемые по формуле (37):

. (50)

Аналогичная формула для случайной величины :

.

Для непрерывных двумерных случайных величин формулы имеют вид:

, . (51)

Ковариацией (или корреляционным моментом) случайных величин и называют математическое ожидание произведения отклонений этих величин от своих математических ожиданий

.

Ковариация характеризует как степень зависимости случайных величин и , так и их рассеяние около своих математических ожиданий и .

Формулы для вычисления ковариации имеют вид

, (52)

(53)

соответственно для двумерного дискретного и непрерывного случайного вектора.

Основные свойства ковариации:

1. .

2. .

3. .

4. Если и независимые случайные величины, то .

Коэффициентом корреляции двух случайных величин и называют отношение их ковариации к произведению средних квадратических отклонений этих величин

. (54)

Основные свойства коэффициента корреляции:

1. .

2. .

3. .

4. Если и независимые случайные величины, то .

Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю.

Из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности случайных величин не следует их независимость.

Линейной средней квадратической регрессией на называют функцию вида

. (55)

Пример 49. Дискретная двумерная случайная величина (, ) задана законом распределения

Табл. 6

	0,15	0,06	0,25	0,04
	0,30	0,10	0,03	0,07

Найти:

1. Условное математическое ожидание составляющей при условии, что =1 (регрессию величины на при ).

2. Математическое ожидание .

3. Дисперсию .

4. Условную дисперсию составляющей при условии, что =1.

Решение. 1. Найдем вероятность того, что . Для этого сложим вероятности, помещенные в первом столбце исходной таблицы

0,15+0,30=0,45.

Определим условные распределения вероятностей величины при :

1/3,

2/3.

Вычисляем искомое условное математическое ожидание по формуле (47) (регрессию величины на при )

5.

2. Чтобы определить , найдем закон распределения (ряд распределения) случайной величины :

	0,5	0,5

Отсюда вычисляем

4,5.

3. Дисперсию найдем по формуле, аналогичной формуле (42)

2,25.

4. Условную дисперсию составляющей при условии, что =1 вычислим по формуле, аналогичной формуле (50):

2.

Пример 50. Задана совместная плотность распределения непрерывной двумерной случайной величины (, ): в квадрате , ; вне квадрата . Найти математическое ожидание и дисперсию составляющей .

Решение. Найдем вначале плотность распределения :

.

Определим математическое ожидание составляющей :

.

Для вычисления определенного интеграла используем формулу интегрирования по частям .

Возьмем следующие части подынтегрального выражения: .

Тогда .

Отсюда

.

Далее вычислим дисперсию по формуле .

.

Тогда

.

Пример 51. Закон распределения дискретной двумерной случайной величины (, ) задан следующей таблицей:

Табл. 7

	-1
	0,10	0,25	0,30	0,15
	0,10	0,05	0,00	0,05

Требуется:

1. Определить ковариацию и коэффициент корреляции случайных величин и .

2. Найти уравнение линейной средней квадратической регрессии на .

Решение. 1. Ковариацию найдем, используя ее свойство 3:

.

На основе исходной таблицы определим законы распределения одномерных случайных величин и :

0,8 0,2

-1       0,2 0,3 0,3 0,2

Полученные законы распределения позволяют вычислить математические ожидания, дисперсии и средние квадратические отклонения случайных величин и :

1,2;

0,5;

1,6;

1,3;

0,16;

1,05;

0,4;

1,025.

Математическое ожидание произведения 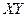найдем по формуле

,

где суммирование производим по всем клеткам исходной таблицы:

0,5.

Далее вычисляем ковариацию

-0,1.

Коэффициент корреляции находим по формуле (54)

-0,244.

Значение -0,244 говорит о том, что между величинами и существует обратная заметная зависимость: при увеличении одной случайной величины другая имеет тенденцию уменьшаться и наоборот.

2. Уравнение линейной регрессии найдем по формуле (55)

-0,625x+1,2502.