 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторное произведение векторов и его свойства
|
|
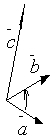
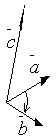 Введем сначала понятие ориентации тройки векторов.
Введем сначала понятие ориентации тройки векторов.
Пусть даны три некомпланарных вектора 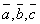 с общим началом, перечисленных в определенном порядке: первый –
с общим началом, перечисленных в определенном порядке: первый –  , второй –
, второй –  , третий –
, третий – 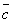 .
.
Тройка некомпланарных векторов 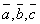 называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора
называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройку векторов называют левой, в этом случае если мы будем смотреть с конца вектора 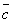 , то кратчайший поворот от
, то кратчайший поворот от  к
к  осуществляется по часовой стрелке.
осуществляется по часовой стрелке.
Векторным произведением векторов  и
и  называется новый вектор
называется новый вектор 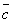 , удовлетворяющий условиям:
, удовлетворяющий условиям:
-
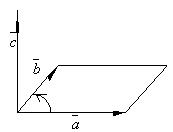 Длина вектора
Длина вектора 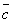 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и  .
. - Вектор
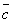 перпендикулярен плоскости этого параллелограмма.
перпендикулярен плоскости этого параллелограмма. - Он направлен так, что векторы
 и
и  образуют правую тройку векторов.
образуют правую тройку векторов.
Векторное произведение векторов  и
и  обозначается символом
обозначается символом 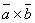 . Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
. Если хотя бы один из сомножителей равен нулю, то векторное произведение по определению считают равным нулю
Векторное произведение обладает следующими свойствами:
- Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:
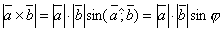 .
.
Таким образом, 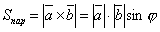 и
и 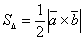 .
.
- При перестановке сомножителей векторное произведение меняет свой знак
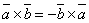 .
.
 Действительно из определения векторного произведения следует, что векторы
Действительно из определения векторного произведения следует, что векторы 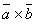 и
и 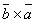 имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы
имеют одинаковые модули, расположены на одной прямой, но направлены в противоположные стороны. Поэтому, векторы 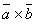 и
и 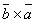 являются противоположными векторами и поэтому
являются противоположными векторами и поэтому 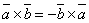 .
.
- Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов
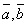
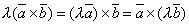 .
.
Доказательство этого свойства непосредственно следует из определения векторного произведения. Докажем для λ > 0. В этом случае 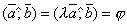 . Тогда по определению векторного произведения
. Тогда по определению векторного произведения
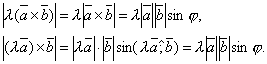
Вектор 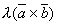 перпендикулярен векторам
перпендикулярен векторам  и
и  . Вектор
. Вектор 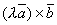 также
также 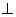 векторам
векторам  и
и  , т.к. векторы
, т.к. векторы  и
и  ,
,  и
и  лежат в одной плоскости. Следовательно, векторы
лежат в одной плоскости. Следовательно, векторы 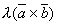 и
и 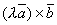 коллинеарны. Очевидно, что направления их также совпадают. Т. к.
коллинеарны. Очевидно, что направления их также совпадают. Т. к. 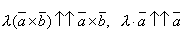 , и следовательно,
, и следовательно, 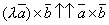 , то
, то  .
.
Поэтому  .
.
Аналогично проводится доказательство для случая λ < 0.
- Для любых векторов
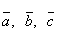 имеет место равенство
имеет место равенство
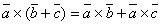 .
.
Примем без доказательства.
- Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.
Действительно, если векторы коллинеарны, то 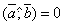 , т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
, т.е. площадь параллелограмма, построенного на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В частности 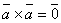 .
.
Примеры.
- Раскрыть скобки
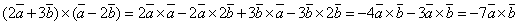 .
.
- Найти площадь треугольника, построенного на векторах
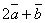 и
и  , если известно, что
, если известно, что 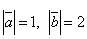 и
и  .
.
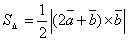 .
.
Найдем 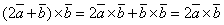 .
.
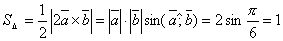 .
.
Можно показать, что если 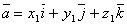 и
и 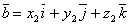 , то координаты векторного произведения векторов
, то координаты векторного произведения векторов  и
и  находятся по формуле:
находятся по формуле:
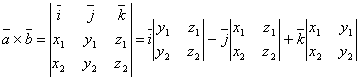 .
.
Примеры.
- Найти векторное произведение векторов
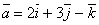 и
и 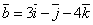 .
.
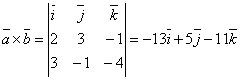 .
.
- Найти площадь
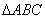 , если A (2; 3; 1), B (-1; -2; 0), C (-3; 0; 1).
, если A (2; 3; 1), B (-1; -2; 0), C (-3; 0; 1).
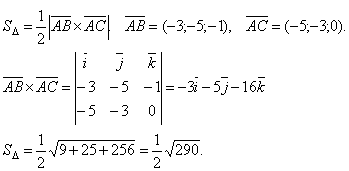
- Даны векторы
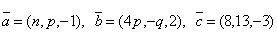 . Найти параметры n, p, q если известно, что векторы
. Найти параметры n, p, q если известно, что векторы  и
и  коллинеарны, а векторы
коллинеарны, а векторы  и
и 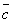 ортогональны.
ортогональны.
Так как векторы  и
и  коллинеарны, то
коллинеарны, то 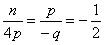 . Векторы
. Векторы  и
и 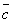 ортогональны, поэтому
ортогональны, поэтому 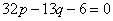 . Итак, получили систему уравнений
. Итак, получили систему уравнений

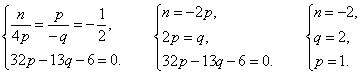
Дата публикования: 2015-11-01; Прочитано: 1082 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
