Уравнение плоскости, проходящей через данную точку

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M₀ (x₀, y₀, z₀), лежащей в плоскости σ.

Вектор перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор имеет координаты .

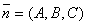Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки M Î σ вектор 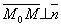.Поэтому их скалярное произведение равно нулю 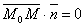. Это равенство – условие того, что точка M Î σ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через 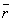радиус-вектор точки M, 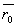– радиус-вектор точки M₀, то 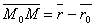и уравнение можно записать в виде

.

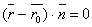Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как 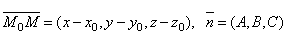, то

.

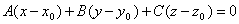Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Примеры.

1. Составить уравнение плоскости, проходящей через точку М (1;-2;3) перпендикулярно вектору .

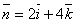Используя выведенное уравнение, получим 2(x -1)+0(y +2)+4(z -3)=0 или x +2 z -7=0.

1. Составить уравнение плоскости, проходящей через точки A (1;2;3), B (-1;0;0), C (3;0;1).

Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор 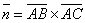. Найдем это вектор. 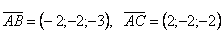. Тогда

.

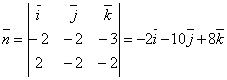Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x -1)-10(y -2)+8(z -3)=0 или x +5 y -4 z +1=0.