 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Необходимый признак существования экстремума (теорема Ферма)
|
|
Теорема 9.2 Если функция y=f(x) непрерывна и дифференцируема в точке x0 и имеет в ней экстремум, то производная в этой точке f'(x)=0 (Рис. 9.4)
Доказательство. Пусть x0 –точка максимума. В этом случае f(x0)> f(x0+ Δ x), независимо от знака Δ x. Тогда Δy=f(x0+Δx)-f(x0)<0, ( Δ x ><0). Если Δ x>0, то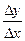 
<0; если Δ x>0, то 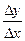>0.
Рис. 9.4
Так как
, 
,
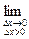
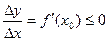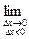
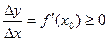то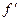 
(x0)=0.
Для случая, когда x0 –точка минимума, доказательство аналогично.
Обратное теореме Ферма утверждение не верно, то есть из условия f'(x)=0, не следует, что x0 –точка экстремума.
Примеры.
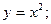
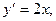
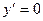при x=0 (Рис. 9.5)
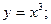
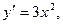
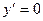при x=0 (Рис. 9.6)
Рис. 9.5 Рис. 9.6
Таким образом, экстремумы функции следует искать среди критических (стационарных) точек. Однако, не всякая стационарная точка является точкой экстремума. Теорема Ферма имеет простое геометрическое истолкование: если x0 –точка экстремума, то касательная к кривой в этой точке параллельна оси Ox.
Замечание. Если снять требование дифференцируемости в точке экстремума x0, то возможно в этой точке функция y=f(x) имеет либо бесконечную производную (f'(x)=∞), либо вообще не имеет производной. (Рис. 9.7)
Острые экстремумы в точках x=0, x=x1, x=x3 и x=x4.
x2 – точка гладкого экстремума.
Рис.9.7
Примеры.
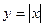(Рис. 9.8 а), 
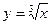(Рис. 9.8 б), 
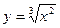(Рис. 9.8 в)
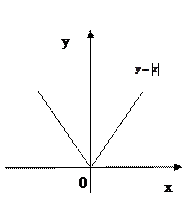
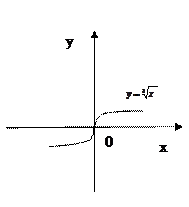
а) б) в)
Рис. 9.8
Дата публикования: 2015-11-01; Прочитано: 937 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
