 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Собственные значения и собственные векторы матрицы
|
|
Число λ называется собственным значением квадратной матрицы А порядка n, если можно подобрать такой ненулевой n -мерный вектор х, что А х = λ х. Множество всех собственных значений матрицы А совпадает с множеством всех решений уравнения | A – λE | = 0, которое называется характеристическим уравнением матрицы А.
Ненулевой вектор х называется собственным вектором квадратной матрицы А, соответствующим ее собственному значению λ, если А х = λ х. Множество всех собственных векторов матрицы А, соответствующих ее собственному значению λ, совпадает с множеством всех ненулевых решений системы однородных уравнений
(A – λE) х = θ:
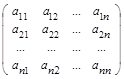
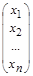 = λ
= λ 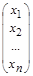 =>
=> 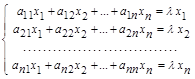 =>
=>
=> 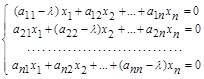 . (1)
. (1)
Данная системы однородных уравнений имеет ненулевое решение, если ее определитель равен нулю:
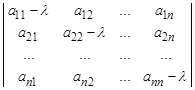 = 0.
= 0.
Это и есть характеристическое уравнение матрицы А.
Множество решений системы (1) обозначим через А (λ).
Пусть λ 1, λ 2, …, λm – различные собственные значения матрицы А и пусть в каждом из множеств А (λ 1), А (λ 2), …, А (λm) выбраны линейно независимые системы векторов. Тогда объединение этих систем будет линейно независимой системой.
Собственные значения диагональной матрицы равны ее диагональным элементам.
Пример 1. Найти собственные значения и собственные векторы матрицы А = 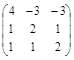 .
.
Р е ш е н и е. Составим характеристическое уравнение
| A – λE | = 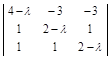 = 0
= 0
или (4 – λ) (2 – λ)2 – 3 – 3 – (4 – λ) + 3(2 – λ) + 3(2 – λ) = 0.
Раскроем скобки и приведём подобные слагаемые – λ 3 + 8 λ 2 – 25 λ + 18 = 0 или
λ 3 – 8 λ 2 + 25 λ – 18 = 0. Отсюда λ 3 – λ 2 – 7 λ 2 + 7 λ + 18 λ – 18 = 0 или
λ 2 (λ – 1) – 7 λ (λ – 1) + 18(λ – 1) = 0.
Вынесем общий множитель за скобки. Тогда получим уравнение (λ – 1) (λ 2 – 7 λ + 18) = 0.
Произведение равно нулю, когда один из сомножителей равен нулю. Получаем совокупность уравнений
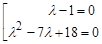 =>
=> 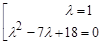
Второе уравнение – квадратное уравнение с отрицательным дискриминантом
D = (–7)2 – 4·18 = 49 – 72 = –23.
Следовательно, оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень λ = 1, а матрица только одно собственное значение
λ = 1. Найдём собственный вектор, принадлежащий этому собственному значению, решая уравнение
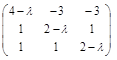
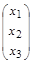 =
=  .
.
Расписывая по компонентам и подставляя λ = 1, получим систему из трёх уравнений с тремя неизвестными:
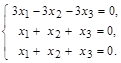
Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде:
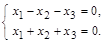
Сложим оба уравнения, а затем из второго вычтем первое. Получим 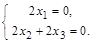 Отсюда
Отсюда
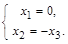
и мы имеем собственный вектор x = 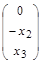 = α
= α 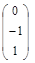 .
.
Пример 2. Найти собственные значения и собственные векторы матрицы 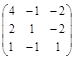 .
.
Р е ш е н и е. 1. Характеристическое уравнение имеет вид
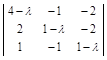 = 0 или λ 3 – 6 λ 2 + 11 λ – 6 = 0.
= 0 или λ 3 – 6 λ 2 + 11 λ – 6 = 0.
Отсюда λ 1 = 1, λ 2 = 2, λ 3 = 3.
2. Находим собственные векторы, соответствующие λ = 1.
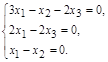
Решая ее, получим x 1 = x 2 = x 3. Собственные векторы, соответствующие собственному значению λ = 1, имеют вид х = α 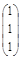 , где α ≠ 0 – произвольная константа.
, где α ≠ 0 – произвольная константа.
Далее рассматриваем случай λ = 2: 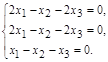
Решая ее, получим x 1 = x 3; x 2 = 0. Собственные векторы, соответствующие собственному значению λ = 2, имеют вид х = α 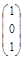 , где α ≠ 0 – произвольная константа.
, где α ≠ 0 – произвольная константа.
Случай λ = 3: 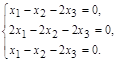
Решая ее, получим x 1 = x 2; x 3 = 0. Собственные векторы, соответствующие собственному значению λ = 3, имеют вид х = α 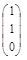 , где α ≠ 0 – произвольная константа.
, где α ≠ 0 – произвольная константа.
Пример 3. Найти собственные значения и собственные векторы матрицы А = 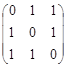 .
.
Р е ш е н и е. Найдем характеристическое уравнение матрицы А:
| A – λE | = 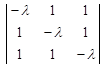 = - λ 3 + 3 λ + 2.
= - λ 3 + 3 λ + 2.
Далее находим корни этого характеристического уравнения - λ 3 + 3 λ + 2 = 0. Разложим левую часть уравнения на множители: – (λ – 2)(λ + 1)2 = 0.
Следовательно, матрица А имеет два собственных значения: λ 1 = 2, λ 2 = -1.
Следующим шагом находим собственные векторы, соответствующие собственному значению λ = 2. Для этого решаем систему уравнений
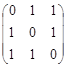
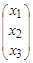 = 2
= 2 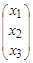 ó
ó 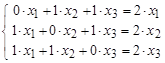 ó
ó 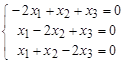 .
.
Получили однородную систему линейных уравнений. Находим ее фундаментальную систему решений:
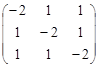
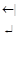 ~
~ 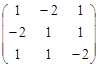
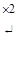
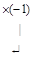 ~
~ 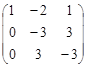
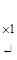 ~
~ 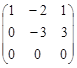
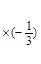 ~
~ 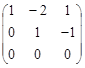 =
=
ð 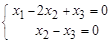 . Общее решение: Х о =
. Общее решение: Х о = 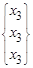 . Свободный член один х 3. Положив
. Свободный член один х 3. Положив
х 3 = 1, получим фундаментальную систему решений, которая состоит из одного вектора 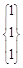 . Т.о., вектор α ·
. Т.о., вектор α · 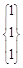 =
= 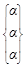 , α
, α 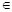 R, – произвольный собственный вектор, соответствующий собственному значению λ = 2.
R, – произвольный собственный вектор, соответствующий собственному значению λ = 2.
Затем находим собственные векторы, соответствующие собственному значению
λ = -1. Для этого решаем систему уравнений
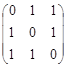
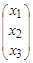 = -
= - 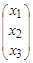 ó
ó 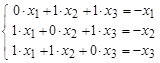 ó
ó 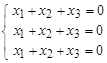 .
.
Получили однородную систему линейных уравнений. Находим ее фундаментальную систему решений:

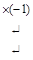 ~
~ 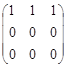 => х 1 + х 2 + х 3 = 0. Общее решение: Х о =
=> х 1 + х 2 + х 3 = 0. Общее решение: Х о = 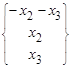 . Полагая последовательно х 2 = 1, х 3 = 0 и х 2 = 0, х 3 = 1, получим фундаментальную систему решений,
. Полагая последовательно х 2 = 1, х 3 = 0 и х 2 = 0, х 3 = 1, получим фундаментальную систему решений,
которая состоит из двух векторов 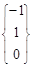 и
и 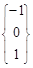 . Т.о., вектор α ·
. Т.о., вектор α · 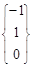 + β
+ β 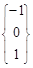 =
= 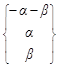 ,
,
α, β 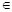 R, – произвольный собственный вектор, соответствующий собственному значению λ = -1.
R, – произвольный собственный вектор, соответствующий собственному значению λ = -1.
Задания. Найти собственные значения и собственные векторы матриц:
1. А 1 = 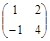 , 2. А 2 =
, 2. А 2 = 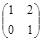 , 3. А 3 =
, 3. А 3 = 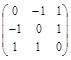 , 4. А 4 =
, 4. А 4 = 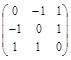 ,
,
5. А 5 = 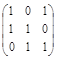 .
.
2.2. Приведение квадратной матрицы к диагональному виду
Матрица А приводится к диагональному виду, если можно подобрать такую невырожденную матрицу T, что Т –1 А Т – диагональная матрица. Матрица А порядка n приводится к диагональному виду тогда и только тогда, когда в пространстве Rn имеется базис, состоящий из собственных векторов матрицы А. Столбцами матрицы T являются координаты векторов этого базиса.
В пространстве Rn имеется базис, состоящий из собственных векторов матрицы А, тогда и только тогда, когда объединение базисов подпространств А (λ 1), А (λ 2), …, А (λm) является базисом пространства Rn, где λ 1, λ 2, …, λm – все различные собственные значения матрицы А.
Правило построения матрицы Т, приводящей матрицу А порядка n к диагональному виду:
1. Найти все собственные значения матрицы А.
2. Для каждого собственного значения λi найти фундаментальную систему решений однородной системы линейных уравнений (A – λi E) х = θ.
3. Построить матрицу T, столбцами которой являются координаты решений всех найденных фундаментальных систем.
4. Если полученная матрица T является квадратной, то она приводит матрицу А к диагональному виду. Если же матрица T не будет квадратной, то матрица А не может быть приведена к диагональному виду.
Пример 1. Найти матрицу Т, которая приводит матрицу А = 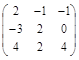 к
к
диагональному виду. Найти матрицу В = Т –1 А Т.
Р е ш е н и е. Вычислим определитель матрицы A – λE:
| A – λE | = 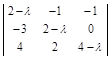 = (2 – λ)2(4 – λ) + 6 + 4(2 – λ) – 3(4 – λ) =
= (2 – λ)2(4 – λ) + 6 + 4(2 – λ) – 3(4 – λ) =
= (2 – λ) ((2 – λ) (4 – λ) + 4) – 3(2 – λ) = (2 – λ) (λ 2 – 6 λ + 8 + 4 – 3) =
= (2 – λ) (λ 2 – 6 λ + 9) = (2 – λ) (λ – 3)2.
Собственные значения матрицы А равны 2 и 3.
Теперь надо найти фундаментальные системы решений систем уравнений (A – 2 E) х = θ и (A – 3 E) х = θ:
Находим собственные векторы, соответствующие λ = 2.
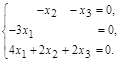 =>
=> 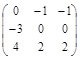
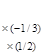
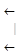 ~
~ 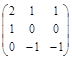
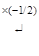 ~
~ 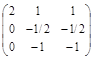
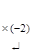 ~
~
~ 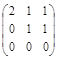 =>
=> 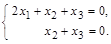 Решая данную систему, получим x 1 = 0, x 2 = – x 3. Фундаментальная система решений состоит из одного вектора
Решая данную систему, получим x 1 = 0, x 2 = – x 3. Фундаментальная система решений состоит из одного вектора 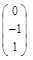 .
.
Далее рассматриваем случай λ = 3:
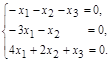 =>
=> 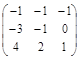
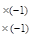 ~
~ 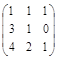
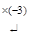
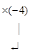 ~
~ 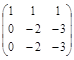
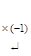 ~
~ 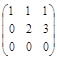
=> 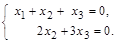 Решая данную систему, получим x 2 = –
Решая данную систему, получим x 2 = – 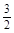 x 3; x 1 =
x 3; x 1 = 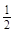 x 3.
x 3.
Фундаментальная система решений состоит из одного вектора 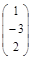 .
.
Следовательно, матрица Т имеет вид: Т = 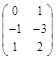 . Полученная матрица не является квадратной, поэтому матрица А не приводится к диагональному виду.
. Полученная матрица не является квадратной, поэтому матрица А не приводится к диагональному виду.
Пример 2. Найти матрицу Т, которая приводит матрицу А = 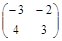 к диагональному
к диагональному
виду. Найти матрицу В = Т –1 А Т.
Р е ш е н и е. Вычислим определитель матрицы A – λE:
| A – λE | = 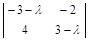 = λ 2 – 9 + 8 = λ 2 – 1 = 0.
= λ 2 – 9 + 8 = λ 2 – 1 = 0.
Собственные значения матрицы А равны –1 и 1.
Теперь надо найти фундаментальные системы решений систем уравнений (A + E) х = θ и (A –E) х = θ:
Находим собственные векторы, соответствующие λ = –1.
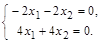 =>
=> 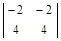
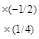 ~
~ 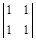
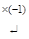 ~
~ 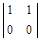 => x 1 + x 2 = 0. Решая данную систему, получим x 1 = – x 2. Фундаментальная система решений состоит из одного вектора
=> x 1 + x 2 = 0. Решая данную систему, получим x 1 = – x 2. Фундаментальная система решений состоит из одного вектора 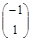 .
.
Далее рассматриваем случай λ = 1:
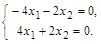 =>
=> 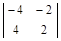
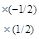 ~
~ 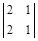
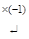 ~
~ 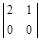 => 2 x 1 + x 2 = 0. Решая данное уравнение, получим x 1 = –
=> 2 x 1 + x 2 = 0. Решая данное уравнение, получим x 1 = – 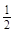 x 2.
x 2.
Фундаментальная система решений состоит из одного вектора 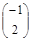 .
.
Следовательно, матрица Т имеет вид: Т = 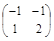 .
.
Ищем обратную к матрице Т: Т –1 = 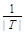
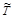 . | T | = –1,
. | T | = –1, 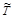 =
= 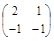 => Т –1 =
=> Т –1 = 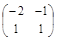 .
.
Матрица В = Т –1 А Т:
Т –1 А = 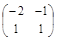
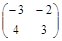 =
= 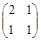 ; Т –1 А Т =
; Т –1 А Т = 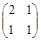
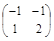 =
= 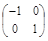 .
.
Задания. Найти матрицу Т, которая приводит данную матрицу А к диагональному виду, и найти матрицу В = Т –1 А Т.
1. А = 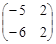 , 2. А 2 =
, 2. А 2 = 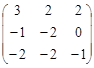 , 3. А 3 =
, 3. А 3 = 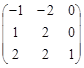 ,
,
4. А 4 = 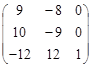 .
.
2.3. Ортогональные и симметрические матрицы
Матрица А Т, столбцами которой являются строки матрицы А, называется транспонированной к А.
Дата публикования: 2015-10-09; Прочитано: 2382 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
