Пример решения матричной игры 3×3

Рассмотрим задачу с матрицей платежей игрока А

Сначала уменьшим размерность задачи.

В данной игре пара стратегий игрока А такова, что при любом ответе противника платежи игрока А при выборе стратегии 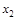меньше, чем при выборе 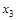. Это позволяет исключить стратегию 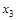из рассмотрения, считая, что вероятность ее выбора равна 0. Таким образом, исходную игру 3×3 мы свели к игре 2×3.

Замечание. Все предлагаемые в вариантах задачи допускают понижение размерности, т.е. исходная игра 3×3 сводится к игре 2×3 или к игре 3×2.

Обозначим вероятность выбора стратегии 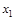- 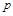. Тогда вероят­ность выбора стратегии 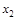будет равна 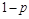. Обозначим вероятность выбора стратегии 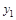- 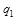, а 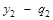. Тогда вероятность выбора стратегии 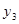будет равна .

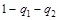Естественные ограничения на введенные переменные задаются системой неравенств

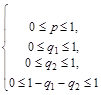
Геометрически, область изменения этих переменных можно пред­ста­вить в виде отрезка (0,1) оси Оp и треугольника ОАВ на плоскости (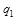, 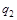). Обозначим 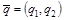, а треугольник ОАВ – Ω.

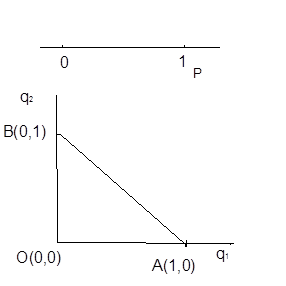
Вычислим математическое ожидание результата игры

.

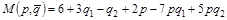Для определения оптимальной стратегии игрока А нужно найти

.

Здесь сначала при каждом фиксированном значении p необхо­ди­мо найти макси­мум по 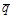, который достигается в одной из вершин треугольника ОАВ, причем положение максимума зависит от значения p. Разобьем область изменения p на интервалы знакопостоянства коэффи­циен­тов пр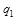и и 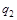. Решим задачу на каждом из этих интервалов и выберем из результатов наилучший для игрока А, т.е. наименьший.

1) 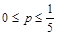. На этом интервале 3-7p>0, -1+5p≤0 и значит максимум достигается в вершине А(1,0). Подставив координаты этой точки, мы получим

2) 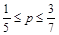. На этом интервале 3-7p≥0 и -1+5p≥0. Это озна­чает, что функционал возрастает при движении по ребрам ОА и ОВ, и для определения максимума нужно сравнить значения функ­цио­нала в вершинах А и В.

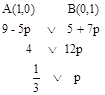
Итак, при p<1/3 значение функционала в т.А больше, чем в т.В, и наоборот. Значит рассматриваемый интервал нужно разбить на два

2а) 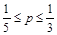. На этом интервале максимум достигается в вершине А(1,0). Подставив координаты этой точки, мы получим

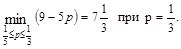
2б) 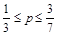. На этом интервале максимум достигается в вершине В(0,1). Подставив координаты этой точки, мы получим

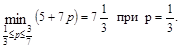
3) 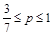. На этом интервале 3-7p≤0, -1+5p≥0 и значит максимум достигается в вершине В(0,1). Подставив координаты этой точки, мы получим

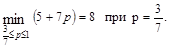
Итак, мы нашли, что наилучший результат для игрока А достигается при 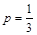, цена игры - .

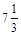Для определения оптимальной стратегии игрока В нужно найти

.

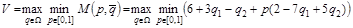Здесь сначала при каждом фиксированном значении 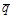необхо­ди­мо най­ти мини­мум по p, который достигается либо при p=0, либо при p=1 в зависимости от знака выражения .

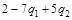Проведем на плоскости 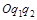прямую 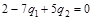. Она раз­делит треугольник ОАВ на две области: четырехугольник OBST и тре­угольник STA (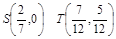). Это области знакопостоянства коэф­фи­циен­та при р в функционале. Обозначим их 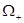и 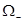по знаку коэффициента. Решим задачу в каждой из этих областей.

1) 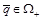. В этом случае минимум по р достигается при р=0, и

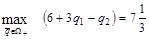, так как в т.О(0,0) функционал равен 6, в т.В(0,1) – 5, в т. 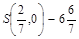, в т. .

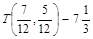2) . В этом случае минимум по р достигается при р=1, и

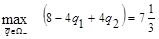, так как в т.А(1,0) функционал равен 4, в т. 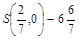, а в т. .

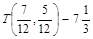Ответ: игроку А нужно стратегию 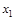выбирать с вероятностью 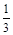, стра­тегию 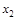выбирать с вероятностью 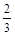, а стратегию 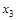не выбирать; иг­ро­ку В нужно стратегию 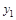выбирать с вероятностью 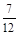, стратегию выбирать с вероятностью 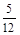, а стратегию 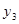не выбирать. Цена игры .

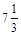Замечание. Игра 3×2 решается аналогично.