Игры двух лиц с нулевой суммой

Пусть в игре участвует два игрока A и Б, партия состоит из одного хода игрока A и ответного хода игрока Б. Ход игрока A заключается в выборе одной из n возможных стратегий 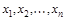. Ход игрока Б со­стоит из выбора одной из m возможных стратегий 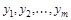. Каждая пар­тия игры состоит в том, что партнеры выбирают по одной своей стра­те­гии, в результате чего опре­де­ля­ют­ся платежи игрокам. Пусть игрок A выбирает стратегию 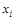, игрок Б - стратегию 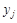. В результате осу­щест­в­ле­ния операции платеж игрока A игроку Б составляет 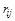, а платеж игро­ка Б игроку A 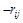. Такая игра яв­ля­ет­ся игрой с нулевой сум­мой, так как выигрыш игрока А равен проигрышу игрока Б.

Игры, для которых сумма платежей одинакова для всех возмож­ных пар­тий, называются играми с нулевой суммой.

Итак, мы рассматриваем конечную игру двух лиц с нулевой сум­мой. Для нее можно составить матрицу платежей, которая пол­нос­тью ха­рактеризует игру.

Игра, заданная платежной матрицей, называется прямоуголь­ной или матричной игрой, приведенной к нормальной форме.

В каждой партии игрок A стремится так выбрать свою стратегию 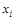, чтобы величина его платежа была минимально возможной. В свою оче­­редь иг­рок Б стремится так выбрать стратегию 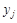, чтобы макси­ми­зи­ро­вать выиг­рыш. Задача состоит в том, чтобы указать опти­маль­ные стра­те­гии каждой сто­роны, т.е. такие стратегии, которые при много­крат­ном повторении игры обеспечивают Б максимально возможный средний вы­иг­рыш, а игроку А - минимально воз­мож­ный средний проигрыш.

Решение игровых задач основывается на принципе минимакса. Этот прин­цип предписывает игрокам выбирать свою стратегию в расчете на наи­худ­ший для себя образ действий противника. Суть этого принципа понятна из сле­дую­щих рассуждений.

Рассмотрим ситуацию с позиции игрока A. На каждую вы­бран­ную стра­те­гию 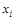игрок Б ответит такой стратегией 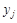, чтобы макси­ми­зи­ро­вать выигрыш

.

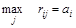Следовательно, из всех возможных стратегий игроку А следует выбрать такую, чтобы минимизировать проигрыш. В этом случае

.

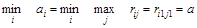Определенная так величина a называется верхней ценой игры или минимаксом, а стратегия - минимаксной стратегией A. Верхняя цена иг­ры - это тот гаранти­ро­ван­ный уровень, больше которого A не заплатит при любом по­ведении Б, если будет применять свою минимаксную стра­те­гию .

Рассмотрим теперь ситуацию с позиции игрока Б. При каждой стратегии 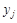сторона A применит такую стратегию 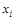, чтобы проиграть как можно меньше:

.

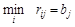Следовательно, наилучший из наихудших для Б вариантов отве­чает такой стратегии 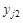, что

.

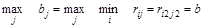Величина b, определенная таким образом, называется нижней це­ной игры или максимином. Нижняя цена игры b - гарантированный вы­иг­рыш Б при любом ответе A.

Если

,

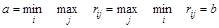то минимаксные стратегии игроков являются оптимальными, т.е. если один из игроков воспользуется минимаксной стратегией, а другой не сле­дует своей минимаксной стратегии, то это может только уменьшить вы­иг­рыш (увеличить проигрыш) этого игрока.

В общем случае .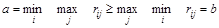

Равновесие пары стратегий определяется для игры двух лиц так же, как и в общем случае игры n лиц. То, что платеж описывается ска­ляр­ной величиной, а не вектором, упрощает дело.

Ситуация равновесия пары стратегий известна так же, как седловая точка.

Def. Седловой точкой называется некоторый элемент мат­ри­цы платежей R такой, что 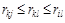при любых i, j.

Таким образом, седловая точка одновременно является наиболь­шим эле­мен­том строки k и наименьшим элементом столбца l.

Если в некоторой игре существует более одной седловой, то пред­став­ляет интерес следующая теорема.

Теорема. Пусть 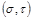и 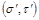- седловые точки. Тогда и 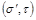также являются седловыми точками и, кроме того .

Кратко данную теорему можно выразить так: седловые точки экви­ва­лентны и взаимозаменяемы.

Следует отметить, что сформулированное свойство не распростра­няется на дру­гие игры, т.е. не выполняется для игр с ненулевой суммой или для игр трех и более лиц.

Теорема. Пусть - седловая точка игры с матрицей R. Тогда 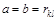. И наоборот, если 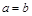, то существует седловая точка , причем .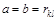

Если 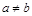, то матричная игра не имеет седловой точки, и мини­макс­ные стратегии не дают решения игры, так как не яв­ля­ют­ся наи­луч­ши­ми ни для одной из сторон. В этом случае гово­рят, что игра не имеет решения в чистых стратегиях.