 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциал функции
|
|
Определение. Функция 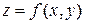 дифференцируема в точке
дифференцируема в точке 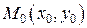 , если её полное приращение в окрестности этой точки представимо в виде
, если её полное приращение в окрестности этой точки представимо в виде
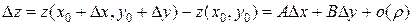 ,
,
где 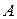 и
и 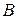 - константы, не зависящие от
- константы, не зависящие от 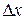 ,
, 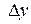 . Здесь
. Здесь
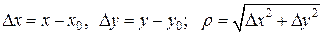 .
.
Если функция 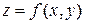 дифференцируема в точке
дифференцируема в точке 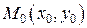 , то в этой точке у нее существуют частные производные, причем
, то в этой точке у нее существуют частные производные, причем 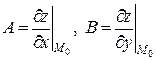 . Обратное, вообще говоря, неверно. В отличие от функций одной переменной, для функций многих переменных из существования в заданной точке первых частных производных не следует дифференцируемость функции по совокупности переменных.
. Обратное, вообще говоря, неверно. В отличие от функций одной переменной, для функций многих переменных из существования в заданной точке первых частных производных не следует дифференцируемость функции по совокупности переменных.
Теорема (достаточное условие дифференцируемости функции двух переменных). Если у функции 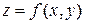 частные производные
частные производные 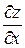 ,
, 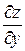 существуют в окрестности точки
существуют в окрестности точки 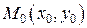 и непрерывны в самой точке
и непрерывны в самой точке 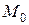 , то функция
, то функция 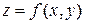 дифференцируема в этой точке.
дифференцируема в этой точке.
В случае дифференцируемости функции главная линейная часть её полного приращения 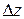 называется первым дифференциалом:
называется первым дифференциалом:
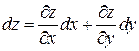 ,
, 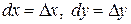 . (1)
. (1)
Пример 1. Найти 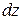 для функции
для функции 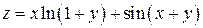 .
.
Решение. Находим частные производные
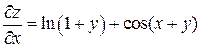 ,
, 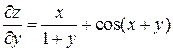 .
.
В соответствии с формулой (1) запишем первый дифференциал:
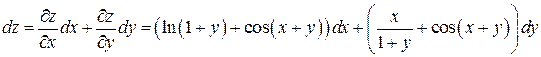 .☻
.☻
Аналогично определяется первый дифференциал функции 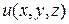 трех переменных:
трех переменных: 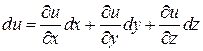 .
.
Пример 2. Найти 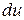 для функции
для функции 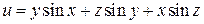 .
.
Решение. Вычислим
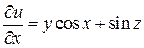 ,
, 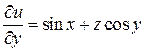 ,
, 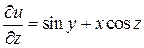 .
.
Первый дифференциал примет вид:
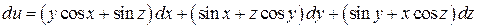 . ☻
. ☻
Заменяя полное приращение функции 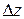 ее дифференциалом
ее дифференциалом 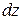 , получим приближенную формулу с точностью до
, получим приближенную формулу с точностью до 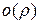 :
:
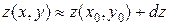 . (2)
. (2)
Пример 3. Вычислить приближенно 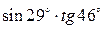 .
.
Решение. Рассмотрим функцию 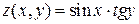 . В качестве начальной точки возьмём
. В качестве начальной точки возьмём 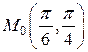 . Тогда
. Тогда 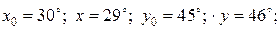
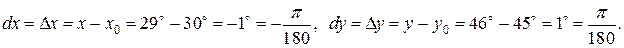 .
.
Вычислим 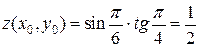 и подсчитаем производные в точке
и подсчитаем производные в точке 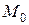 :
:
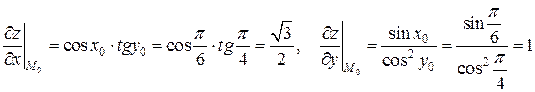 .
.
Запишем первый дифференциал в точке 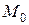 :
:
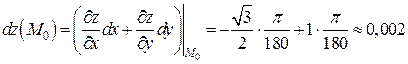 .
.
Теперь в соответствии с приближенной формулой (2) получаем
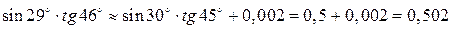 . ☻
. ☻
Дифференциалы более высокого порядка от функции 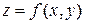 определяются по индукции:
определяются по индукции: 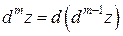 .
.
Для вычисления старших дифференциалов удобно пользоваться символической формулой
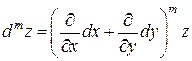 (3)
(3)
При 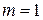 эта формула принимает знакомый вид (1):
эта формула принимает знакомый вид (1):
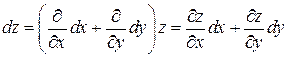 .
.
Если 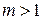 , то при использовании символической формулы (3) применяют бином Ньютона. Например, при
, то при использовании символической формулы (3) применяют бином Ньютона. Например, при 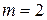 получаем (с учетом равенства непрерывных смешанных производных)
получаем (с учетом равенства непрерывных смешанных производных)
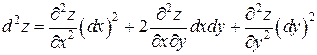 .
.
Если 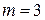 , то
, то
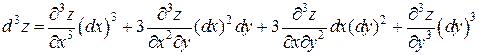 .
.
Аналогично определяются формулы для дифференциалов более высокого порядка от функции 3-х переменных 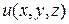 :
:
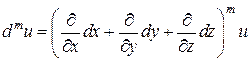
Пример 4. Найти второй дифференциал для функции 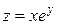 .
.
Решение. Записываем формулу для второго дифференциала
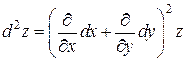
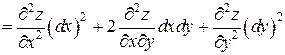 .
.
Остается подсчитать все производные второго порядка. Сначала находим первые производные: 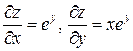 . Подсчитаем вторые производные:
. Подсчитаем вторые производные:
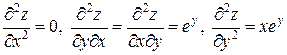 .
.
Следовательно, 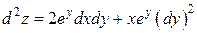 . ☻
. ☻
Дата публикования: 2015-10-09; Прочитано: 263 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
