 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формула Тейлора для функций двух переменных
|
|
Если функция 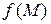 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 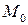 непрерывные частные производные до (
непрерывные частные производные до (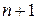 )-го порядка включительно, то в этой окрестности справедлива формула Тейлора
)-го порядка включительно, то в этой окрестности справедлива формула Тейлора
 (1)
(1)
Для функции одной переменной 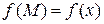 имеем
имеем
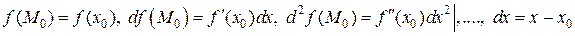
и формула (1) принимает знакомый вид
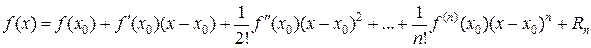
Для функции двух переменных 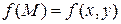 в формуле (1)
в формуле (1)
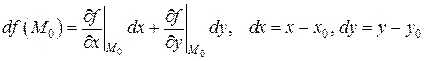
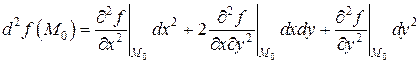 и т.д.,
и т.д.,
то есть дифференциал 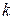 -го порядка
-го порядка 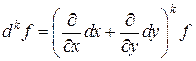 берется в точке
берется в точке 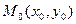 .
.
Остаточный член 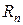 в форме Лагранжа имеет вид
в форме Лагранжа имеет вид
 ,
,
Здесь производные берутся в некоторой средней точке 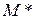 :
:
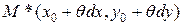 ,
, 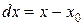 ,
, 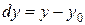 ,
, 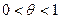 .
.
Остаточный член в форме Пеано (при более слабых предположениях).
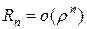 ,
, 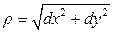 .
.
Пример 1. Для функции 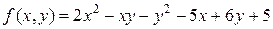 записать формулу Тейлора в окрестности точки
записать формулу Тейлора в окрестности точки 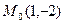 .
.
Решение. Подсчитаем 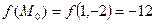 и частные производные:
и частные производные:
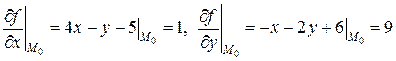
Запишем первый дифференциал в точке 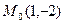 :
:
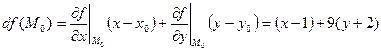 .
.
Найдем вторые производные: 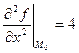 ,
, 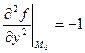 ,
, 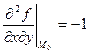 .
.
Запишем второй дифференциал в точке 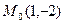 :
:
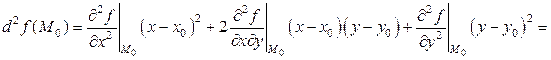
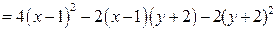 .
.
Все производные порядка выше второго равны нулю. Формула Тейлора принимает вид 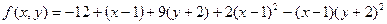 . Фактически мы перегруппировали данный многочлен по степеням
. Фактически мы перегруппировали данный многочлен по степеням 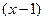 и
и 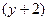 . ☻
. ☻
Пример 2. Записать формулу Тейлора 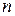 -го порядка для функции
-го порядка для функции 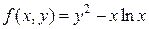 в окрестности точки
в окрестности точки 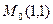 .
.
Решение. Находим 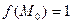 и частные производные:
и частные производные:
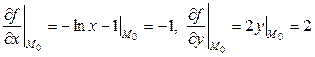 .
.
Запишем первый дифференциал в точке 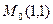 :
:
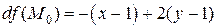 .
.
Подсчитаем вторые производные:
 ,
,  ,
, 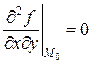 .
.
Теперь можем записать второй дифференциал в точке 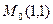 :
:
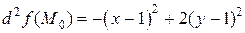 .
.
Продолжаем дифференцировать: 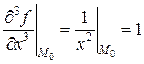 . Все остальные производные 3-го порядка равны нулю:
. Все остальные производные 3-го порядка равны нулю: 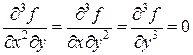 .
.
Значит, из третьего дифференциала в точке 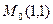 остается одно слагаемое:
остается одно слагаемое:
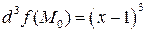 .
.
Легко заметить, что дальнейшее дифференцирование по 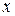 приводит к формуле
приводит к формуле 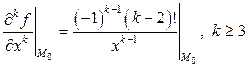 . Значит,
. Значит, 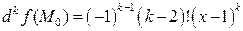 .
.
Формула Тейлора принимает вид:
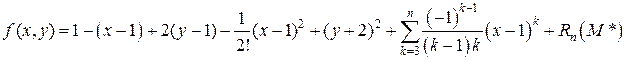 ,
,
где 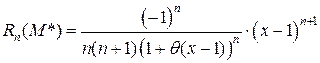 ,
, 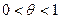 . ☻
. ☻
В частном случае при 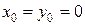 из (1) получаем формулу Маклорена.
из (1) получаем формулу Маклорена.
Пример 3. Функцию 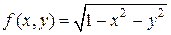 разложить по формуле Маклорена до членов второго порядка.
разложить по формуле Маклорена до членов второго порядка.
Решение. Для формулы Маклорена следует записать разложение (1) в окрестности точки 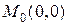 . Находим
. Находим 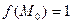 .
.
Для первого дифференциала находим
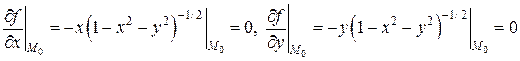 .
.
Так как 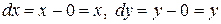 , то
, то 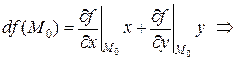
 .
.
Чтобы записать второй дифференциал, находим
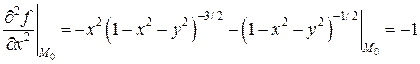
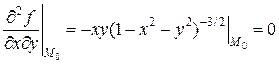
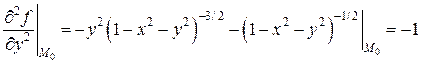 .
.
Получаем 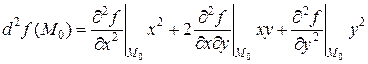
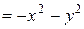 .
.
Формула Маклорена для функции  принимает вид
принимает вид
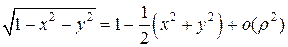 ,
,  . ☻
. ☻
Дата публикования: 2015-10-09; Прочитано: 1968 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
