Фазовая плоскость. Бегущие волны

В упражнениях 1 и 2 мы получали решения заданных уравнений, используя подстановку значений в готовую формулу. При этом область решения определялась автоматически по полученному графику. В этом подразделе мы рассмотрим детально поведение полученных решений из упражнений 1 и 2.

При аналитическом решении задачи предварительно всегда проводят анализ будущего решения, выявляя подобласти с определенными его свойствами. Для выявления характера решения задачи удобно воспользоваться плоскостью состояний 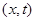или фазовой плоскостью.

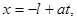
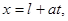
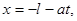
Пусть начальное отклонение струны и/или начальный импульс локализованы в области [- l, l ]. Проведем через концы отрезка локализации прямые 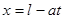. Такие прямые называют характеристиками. Получим картину, аналогичную представленной на рис.П.2.

Рис.П.2. Фазовая плоскость для случая l = 1, a = 1.

Полуплоскость t >0 разбивается на шесть областей. Рассмотрим поведение решения в каждой из них отдельно.

Сначала рассматриваем случай нулевой начальной скорости ψ(y) = 0. Решение задачи будет представлять собой комбинацию двух «бегущих волн», каждая из которых описывается функцией u = φ(x)/2. Первая волна будет «бежать» влево и ее границы будут всегда совпадать с характеристиками, изображенными пунктиром, вторая волна будет «бежать» вправо и ее границы будут совпадать с характеристиками, изображенными сплошными линиями.

В областях 1, 3 и 6 в этом случае колебаний не будет; в области 2 будет только левая волна; в области 5 только правая; в области 4 колебания будут являться суммой двух волн.

Пример П.4. Пусть дана задача Коши для неограниченной струны:

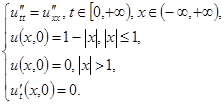
Фазовая плоскость для этой задачи совпадает с фазовой плоскостью на рис.П.2. Построим графики решения задачи для моментов времени t = 0; t = 0.5; t = 1 и t = 1.5, воспользовавшись представлением решения в виде комбинации двух бегущих волн.

Программа для построения данных графиков будет иметь вид:

a=1;

l=1;

dx=0.01;

x=-4*l:dx:4*l;

% Сначала задаем значения по формуле без учета границы:

u=l-abs(x);

u(abs(x)>l)=0; % Затем просто обнуляем лишнее

u_left=0.5*u; % Левая волна

u_right=0.5*u; % Правая волна

for t=0:0.5:1.5

subplot(2,2,2*t+1);

hold on;

u1=circshift(u_left,[0 -a*t/dx]); % Сдвиг левой волны влево

u2=circshift(u_right,[0 a*t/dx]); % Сдвиг правой волны вправо

plot(x,u1,'k-'); % Левая волна (сплошная линия)

plot(x,u2,'k--'); % Правая волна (штриховая линия)

plot(x,u1+u2,'k:') % Сумма волн (пунктирная линия)

xlim([-4*l 4*l]);

ylim([0 1]);

grid on;

xlabel('x');

ylabel('u');

title(['t=' num2str(t)]);

end

Результат выполнения программы представлен на рис.П.3.

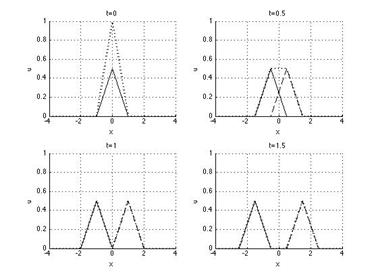
Рис.П.3. Графики бегущих волн

Теперь рассмотрим случай нулевого начального отклонения φ(x) = 0. В этом случае характерные области сохраняются те же, но форма решения будет описываться более сложным образом.

В областях 1 и 6, как и в первом случае, колебаний не будет.

В области 2 будет наблюдаться бегущая влево волна, форма которой в нулевой момент времени описывается уравнением

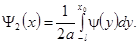
В области 5 будет наблюдаться бегущая вправо волна, форма которой в нулевой момент времени описывается уравнением

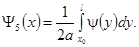
В области 3 решение будет задано константой, равной значению интеграла

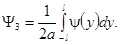
Значение интеграла в области 3 совпадает со значениями на границе областей 2 и 5. Наиболее сложная форма решения в области 4. В зависимости от x она описывается уравнением:

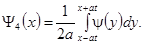
В общем случае, когда и начальное отклонение и начальная скорость не равны нулю, решение описывают как комбинацию двух решений: первое – это комбинация двух бегущих волн, созданных начальным отклонением, второе – это решение, зависящее только от начальной скорости.

Упражнение 4. Дана задача Коши для неограниченной струны:

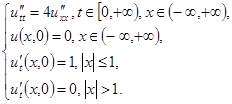
Построить фазовую плоскость для данной задачи и графики решения для моментов времени 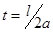, , 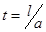. Для построения воспользоваться построенной фазовой плоскостью и представлением в виде бегущих волн для характерных областей.