Волновые уравнения

В этой лабораторной работе мы переходим к изучению методов решения уравнений в частных производных. Рассмотрим задачу Коши для уравнения колебаний струны (волнового уравнения).

Нашей целью будет познакомиться с аналитическими методами решения данной задачи и провести расчеты в среде MATLAB.

Задача Коши для неограниченной струны.

Рассмотрим одномерную бесконечную струну. Пусть в начальный момент времени струну отклонили от равновесного положения (придали некоторую начальную форму) и/или приложили некоторый распределенный импульс к точкам струны.

Последующие колебания струны описываются следующей системой уравнений, получившей название задачи Коши для волнового уравнения:

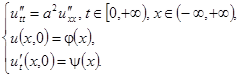
Известно, что решение данной задачи можно найти с помощью формулы Даламбера:

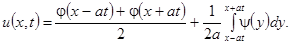
Для упрощения вычислений по данной формуле воспользуемся средствами MATLAB.

Пример П.1. Дана задача Коши для неограниченной струны:

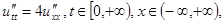
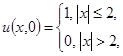
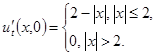
Найти решение задачи при x = 4 в момент времени t = 2.

Сначала создадим две вспомогательные файл-функции для вычисления начального отклонения φ(x) и начальной скорости ψ(x).

Функция для начального отклонения будет иметь вид:

function u = u0(x)

u=zeros(size(x));

L = abs(x) <= 2;

u(L) = 1;

end

Функция для начальной скорости будет иметь вид:

function u = u_t0(x)

u=zeros(size(x));

L = abs(x) <= 2;

u(L) = 2-abs(x(L));

end

Обратите внимание, что созданные функции будут работать правильно и в том случае, если х будет являться не числом, а массивом чисел. Данное свойство понадобится нам в дальнейшем при вычислении интеграла от начальной скорости (второе слагаемое в формуле Даламбера).

Сохраним написанные функции в файлы с именами u 0. m и u _ t 0. m, соответственно.

Выполним расчет по формуле Даламбера при заданных параметрах x, t, a:

x = 4;

t = 2;

a = 2;

u = (u0(x-a*t)+u0(x+a*t))/2+quad(@u_t0,x-a*t,x+a*t)/(2*a)

Для удобства последующего использования реализацию вычислений по формуле можно поместить в отдельный файл-функцию с параметрами x, t, a.

Для реализации интегрирования мы воспользовались встроенной функцией численного вычисления интеграла (quad), которая дает приближенное значение интеграла. Первым недостатком данной встроенной функции является возможность появления шума, связанного с ошибками интегрирования, иногда приводящего к неожиданным результатам.

Для повышения точности в случае относительно простых функций можно вычислять интеграл аналитически с помощью символьных функций, либо вычислить его точное значение вручную.

Вторым существенным недостатком функции quad является то, что ее параметры x и t обязательно должны быть скалярными величинами. В результате для вычисления зависимости решения от x при фиксированном t (или наоборот) требуются вычисления решения в цикле.

Пример П.2. Для задачи Коши из примера П.1 найти решение при произвольном значении x ϵ[–3,3] в момент времени t = 2.

Создадим файл-функцию для реализации вычисления решения по формуле Даламбера с учетом того, что переменная x может быть задана в виде массива.

function u = dalamber(a,x,t)

u = [ ];

for i=x

u_i = (u0(i- a*t)+u0(i + a*t))/2 + quad(@u_t0, i - a*t, i + a*t)/(2*a);

u = [u, ui];

end

end

Вызов написанной функции для расчета будет достаточно простой:

u = dalamber(2,-3:0.01:3,2)

Упражнение 1. В области –∞< x <+∞, 0≤ t <+∞ найти решение уравнения колебания струны (a = 2, l = 2), удовлетворяющее условиям

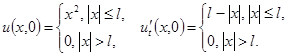
С помощью скрипта из примера П.2 решить данную задачу Коши для произвольных x и моментов времени t = 1, 2, 5, 10. Построить графики, отображающие полученные решения.

Замечания. 1. При выборе отрезка по x необходимо задавать его границы так, чтобы на данном отрезке была представлена вся ненулевая часть решения в заданный момент времени.

2. На всех графиках желательно задать одинаковые границы по обеим осям для корректного сравнения результатов.

3. В этом и последующих упражнениях вместо данной задачи Коши можно использовать задачу из индивидуального задания (по согласованию с преподавателем).

Задача Коши для полуограниченной струны. Метод продолжений.

Теперь рассмотрим полуограниченную струну, закрепленную на одном конце.

Существуют два основных способа закрепления струны: жесткое и свободное закрепление.

В случае жесткого закрепления на конце струны ставят дополнительное условие 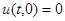. В результате рассматривают задачу Дирихле вида:

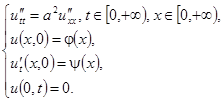
Для решения данной задачи используют метод продолжений, заключающийся в том, что функци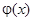и и 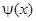продолжают в отрицательную область нечетным образом. В итоге получаем модифицированную формулу Даламбера:

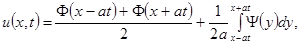
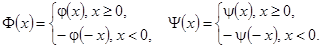
Теперь рассмотрим так называемое свободное закрепление. В этом случае дополнительное условие на границе ставится таким образом, чтобы конец струны оставался всегда параллелен оси x. Таким образом, приходим к задаче Неймана для струны:

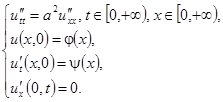
Для решения данной задачи используют метод продолжений, заключающийся в том, что функции φ(x) и ψ(x) продолжают в отрицательную область четным образом. В итоге получаем модифицированную формулу Даламбера:

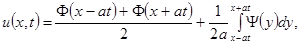
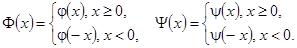
Упражнение 2. В области 0≤ x <+∞, 0≤ t <+∞ найти решение уравнения колебания струны (a = 2, l = 2), удовлетворяющее условиям

Построить графики решения для моментов времени , , .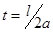

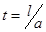Рассмотреть два случая: жесткое закрепление струны (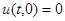) и свободное закрепление струны (u'_x (0, t) = 0). Интервал отображения по оси x выбрать равным [0, 2 l ].