Упражнения. Решить уравнение теплопроводности при заданных начальных и граничных условиях:

Решить уравнение теплопроводности при заданных начальных и граничных условиях:

3.1.

Ответ: .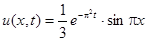

3.2.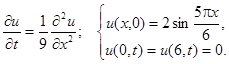

Ответ: .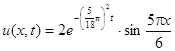

3.3.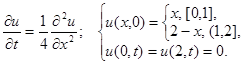

Ответ: .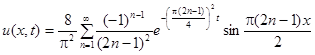

3.4.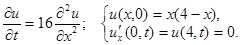

Ответ: .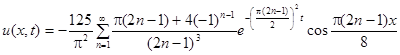

3.5.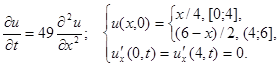

Ответ: .

3.3. Уравнение Лапласа

При исследовании стационарных процессов различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа

.

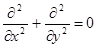Функция u называется гармонической в области Г, если она непрерывна в этой области вместе со своими производными до 2-го порядка и удовлетворяет уравнению Лапласа.

При изучении свойств гармонических функций были разработаны различные математические методы, оказавшиеся плодотворными и в применении к уравнениям гиперболического и параболического типов. Мы будем искать решение краевых задач для простейших областей методом разделения переменных. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных в случае некоторых простейших областей (круг, прямоугольник, шар, цилиндр и др.). Рассмотрим некоторые из них.

Задача Дирихле для уравнения Лапласа в круге

Найти функцию u, удовлетворяющую уравнению Лапласа внутри круга и граничному условию 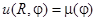на границе круга, где - заданная функция, - полярный угол.

Введем полярную систему координат с началом в центре круга:

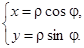
Уравнение Лапласа в полярных координатах имеет вид

.

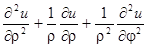Решим уравнение методом разделения переменных, т.е. будем искать частное решение уравнения в виде

.

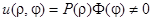Подставляя предполагаемую форму решения в уравнение в полярных координатах, получим:

.

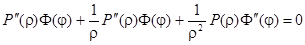Отсюда

.

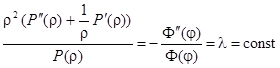Получим два обыкновенных дифференциальных уравнения:

Определим знак .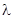

1. Пусть 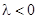, например .
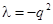Рассмотрим уравнение

.

Характеристическое уравнение имеет вид

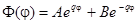- это решение не подходит, так как при изменении угла на величину 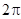однозначная функция 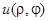должна вернуться к исходному значению (условие периодичности).

Отсюда следует, что 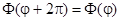, т.е. 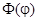является периодической функцией угла с периодом .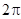

2. Пусть , тогда .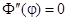

- это решение подходит при условии .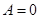

Рассмотрим второе уравнение системы:

.

Пусть

,

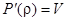тогда

.

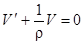Получаем: 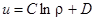- решение уравнения в общем случае.

3. Пусть 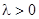, например .
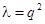Тогда решение уравнения :

.

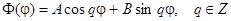Рассмотрим второе уравнение системы

.

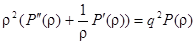Функцию 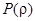будем искать в виде .

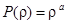Тогда уравнение принимает вид

;

;

;

.

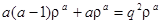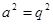Следовательно, 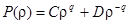- решение уравнения, где С и D - постоянные.

Для решения внутренней задачи надо положить 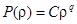, так как, если 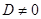, то функция обращается в бесконечность при 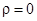и не является гармонической функцией внутри круга. Итак, частные решения нашей задачи найдены:

.

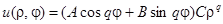Вид общего решения

.

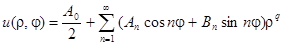Удовлетворим краевому условию:

.

Считая, что задана как функция угла , возьмем ее разложение в ряд Фурье:

,

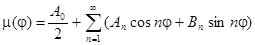где

;

;

.

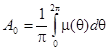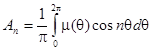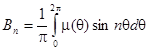Будем использовать формулы Эйлера:

;

.

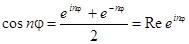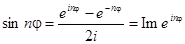Подставляя выражения для коэффициентов Фурье в решение и меняя порядок суммирования и интегрирования, получим:

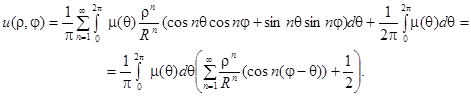
Подставляя в это выражение фомулы Эйлера, получаем интегральную формулу, дающую решение задачи

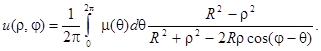
Задача Дирихле для уравнения Лапласа в кольце

Найти функцию u, удовлетворяющую уравнению 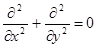внутри кольца.

Необходимо поставить краевые условия на каждой из границ:

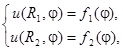
где 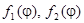- заданные функции, - полярный угол.

Для простоты вычислений возьмем 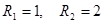и 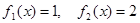, тогда краевые условия примут вид

Из уравнения Лапласа в полярных координатах получаем систему обыкновенных дифференциальных уравнений

Необходимо определить знак .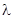

В уравнении Лапласа в круге мы выяснили, что при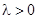

;

, .

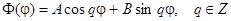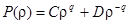И при 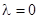получили

, .

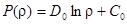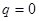Общее решение имеет вид

.

Удовлетворим краевым условиям. Необходимо выяснить, какие из коэффициентов являются лишними.

;

;

;

;

;

;

;

.

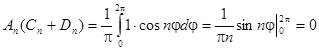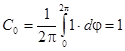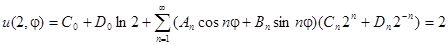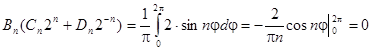Итак, получили

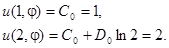
Отсюда

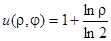– решение задачи.