 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Упражнения. Решить уравнение колебания бесконечной струны, удовлетворяющее условиям
|
|
Решить уравнение колебания бесконечной струны, удовлетворяющее условиям:
2.1. 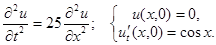
Ответ: 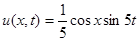 .
.
2.2. 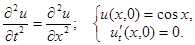
Ответ:  .
.
2.3. 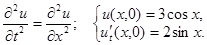
Ответ:  .
.
2.4. 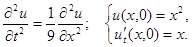
Ответ: 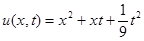 .
.
2.5. 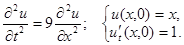
Ответ: 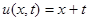 .
.
2.6. 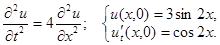
Ответ: 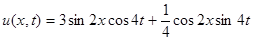 .
.
2.7. 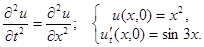
Ответ: 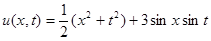 .
.
2.8. 
Ответ: 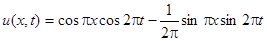 .
.
Решить уравнение колебания полубесконечной струны 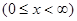 , удовлетворяющее условиям:
, удовлетворяющее условиям:
2.9. 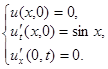
Ответ: 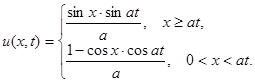
2.10. 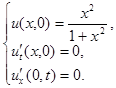
Ответ: 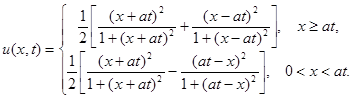
2.11. 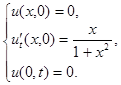
Ответ: 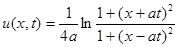 .
.
2.12. 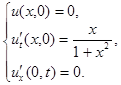
Ответ: 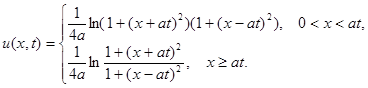
2.13. 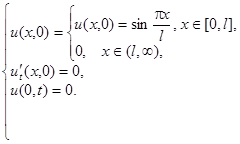
Ответ:
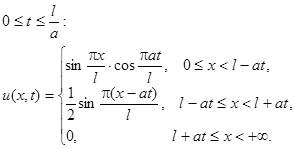
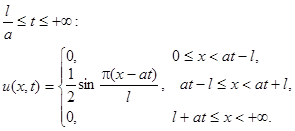
Решить уравнение колебания бесконечной струны, удовлетворяющее условиям:
2.14. 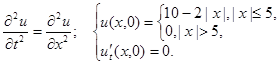
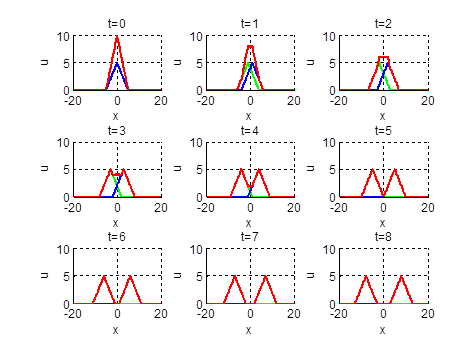
Нарисовать профиль струны для моментов времени 
Ответ:
2.15. 
Нарисовать профиль струны для моментов времени 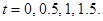
Ответ:
2.16. 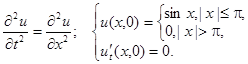
Нарисовать профиль струны для моментов времени 
Ответ:
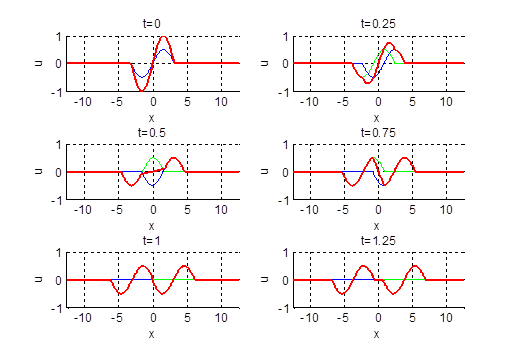
2.17. 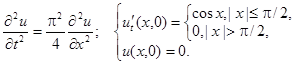
Нарисовать профиль струны для моментов времени 
Ответ:
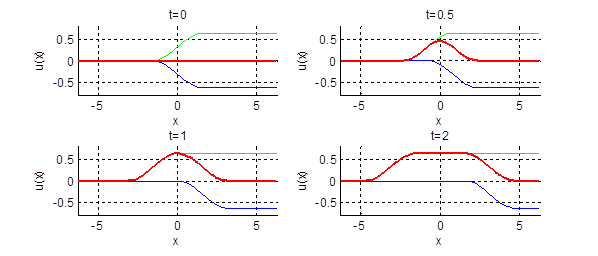
2.18. 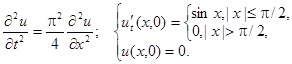
Нарисовать профиль струны для моментов времени 
Ответ:
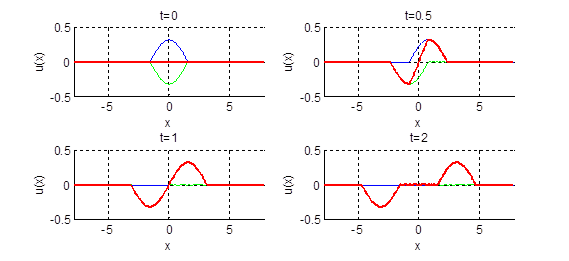
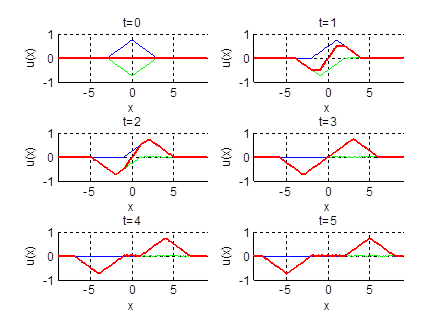
2.19. 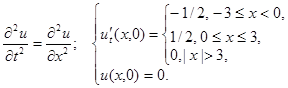
Нарисовать профиль струны для моментов времени 
Ответ:
2.3. Метод Фурье (метод стоячих волн) или метод разделения переменных
Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений с частными производными. Суть этого метода мы продемонстрируем на примере задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение волнового уравнения с начальными и граничными условиями:
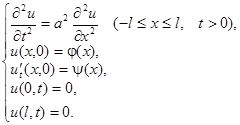
Уравнение линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться с помощью суммирования их с некоторыми коэффициентами найти искомое решение. Частные решения будем искать в виде:
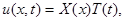
где X (x) – функция только переменного x; T (t) – функция только переменного t.
Подставляя предполагаемую форму решения в уравнение, получим:
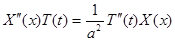
или, после деления на 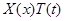 ,
,
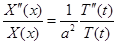 .
.
Правая часть этоого равенства является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение:
 ,
,
где 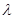 – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций 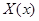 и
и  :
:
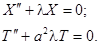
Очевидно, что нас интересуют нетривиальные решения (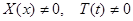 ).
).
Граничные условия дают:
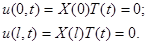
Отсюда следует
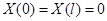 .
.
Таким образом, мы приходим к простейшей задаче: найти те значения параметра 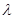 , при которых существуют нетривиальные решения задач:
, при которых существуют нетривиальные решения задач:
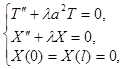
а также найти эти решения. Такие значения параметра 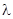 называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи. Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи. Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр 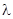 отрицателен, равен нулю или положителен.
отрицателен, равен нулю или положителен.
1. При 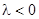 задача не имеет нетривиальных решений. Действительно, общее решение уравнения
задача не имеет нетривиальных решений. Действительно, общее решение уравнения 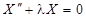 имеет вид
имеет вид
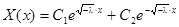 ,
,
Граничные условия дают:
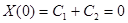 ;
;
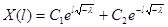 .
.
Отсюда 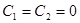 и, следовательно,
и, следовательно,  .
.
2. При 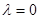 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
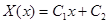 .
.
Граничные условия дают:
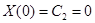 ;
;
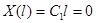 .
.
Отсюда 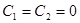 и, следовательно,
и, следовательно,  .
.
3. При 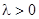 общее решение уравнения может быть записано в виде
общее решение уравнения может быть записано в виде
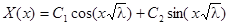 .
.
Граничные условия дают:
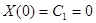 ;
;
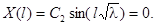
Нетривиальное решение получаем только в случае 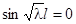 или
или 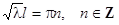 . Отсюда
. Отсюда
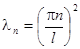 .
.
Этим собственным значениям соответствуют собственные функции
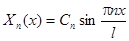 ,
,
где  – произвольная постоянная.
– произвольная постоянная.
Пусть 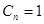 , тогда собственными функциями являются
, тогда собственными функциями являются
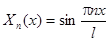 .
.
Аналогично решаем уравнение относительно  :
:
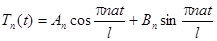 ,
,
где 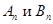 – произвольные постоянные.
– произвольные постоянные.
Следовательно, функции
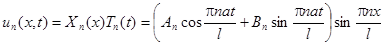
являются частными решениями данного уравнения. В силу линейности и однородности уравнения сумма частных решений также удовлетворяет этому уравнению и граничным условиям. Получаем общее решение:
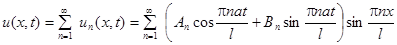 .
.
Начальные условия позволяют определить 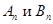 :
:
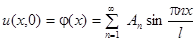 ;
;
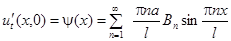 .
.
Из теории рядов Фурье известно, что коэффициенты разложения в ряд Фурье вычисляются по формулам:
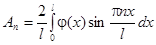 ;
;
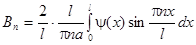 .
.
Подставив эти коэффициенты в общее решение, мы удовлетворим краевым условиям и получим решение уравнения.
Простейшие задачи Штурма – Лиувилля для уравнения 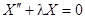 .
.
| Вид условия | Собственные значения и функции |
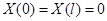
| 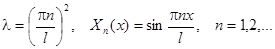
|
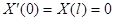
| 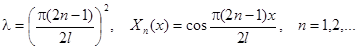
|
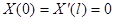
| 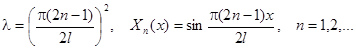
|
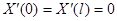
| 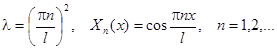
|
Пример. Решить уравнение колебания ограниченной струны 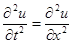 , удовлетворяющее условиям:
, удовлетворяющее условиям: 
Решение. Общее решение имеет вид
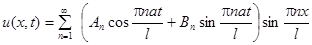 .
.
Из начальных условий определим 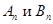 :
:
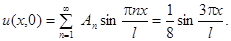
Тогда 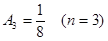 .
.
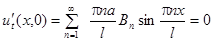 .
.
Отсюда 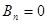 .
.
Подставив эти коэффициенты в общее решение, получим решение уравнения:
 .
.
Можно построить в среде MATLAB поверхность 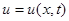 решения данного волнового уравнения (рис.2.6).
решения данного волнового уравнения (рис.2.6).
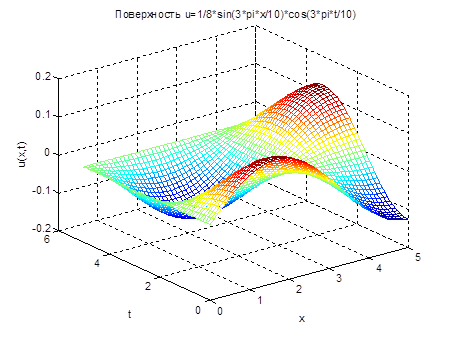
Рис.2.6. Поверхность решения уравнения колебания ограниченной струны
[x,t]=meshgrid(0:.1:5);
u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10);
mesh(x,t,u)
xlabel('x')
ylabel('t')
zlabel('u(x,t)')
title('u=1/8*sin(3*pi*x/10)*cos(3*pi*t/10)')
Для лучшей визуализации напишем m-файл, который с частотой в 1 с будет демонстрировать графики решения рассмотренного выше волнового уравнения для различных моментов времени t (рис.2.7):
figure,axis([0 10 -0.15 0.15]),grid
hold on
x=0:.1:10;
t=0:.4:2;
color=rand(3,length(t));%случайный выбор цветов волн
for k=1:length(t)
u=1/8*sin(3*pi*x/10)*cos(3*pi*t(k)/10);
plot(x,u,'LineWidth',2,'Color',color(:,k))
xlabel('x')
ylabel('u(x)')
title('Колебание струны u=1/8*sin(3*pi*x/10)*cos(3*pi*t(k)/10)')
legend('t=0','t=0.4','t=0.8','t=1.2','t=1.6','t=2')
pause(1)
end
Рис.2.7. График профиля колебания ограниченной струны 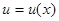 для различных моментов времени
для различных моментов времени
Построим анимацию в среде MATLAB колебаний конечной закрепленной на концах струны при начальных условиях, заданных в предыдущем примере:
x=0:.1:10;
for t=0:20;
u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10);
plot(x,u,'r','LineWidth',2);
hold all;
xlim([0 10]);
ylim([-1/8 1/8]);
grid on;
xlabel('x');ylabel('u(x)');
M(t+1)=getframe;
pause(.2)
hold off;
end
movie(M,3)%повторяем 3 раза
Пример. Решить уравнение колебания ограниченной струны:

Решение. Имеем задачу свободных колебаний струны, закрепленной на концах (в точках 0 и 2). Здесь 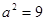 , т.е.
, т.е. 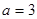 ,
, 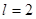 . Поэтому решение ищем в виде:
. Поэтому решение ищем в виде:
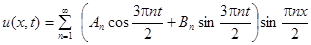 .
.
Подставим t = 0:
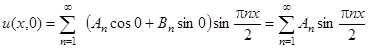 .
.
Используя первое начальное условие, получаем:
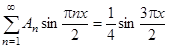 .
.
Можно подобрать коэффициенты An так, чтобы равенство выполнялось тождественно: 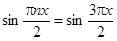 при
при 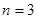 , следовательно,
, следовательно,  .
.
Чтобы использовать второе начальное условие, продифференцируем u (x, t) по t:

и подставим t = 0:
 .
.
Таким образом, получаем условие
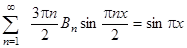
и подбираем коэффициенты:
 при
при 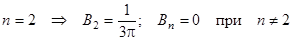 .
.
Итак, имеется всего два ненулевых слагаемых:
при 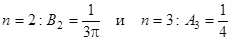 . Окончательно, получаем решение:
. Окончательно, получаем решение:
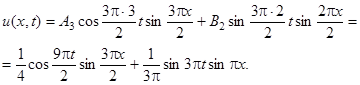
Замечание. Часто начальная скорость точек струны y(х) = 0 (т.е. рассматриваются колебания струны, которую в начальный момент времени оттянули и отпустили без рывка), тогда, очевидно, Вn = 0.
Пример. Решить уравнение колебания ограниченной струны:
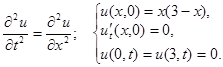
Решение: Имеем задачу свободных колебаний струны, закрепленной на концах (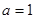 ,
, 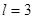 ). Поэтому решение ищем в виде:
). Поэтому решение ищем в виде:
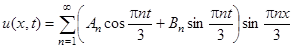 .
.
Используем первое начальное условие:
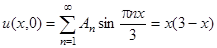 .
.
Подобрать коэффициенты An здесь нельзя, будем их вычислять как коэффициенты Фурье разложения функции  на интервале (0, 3) по синусам:
на интервале (0, 3) по синусам:

Второе начальное условие тривиально, поэтому Bn = 0. Таким образом,
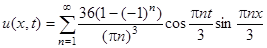 .
.
Заметим, что при 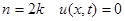 , тогда
, тогда
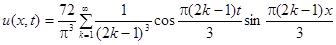 .
.
Дата публикования: 2015-10-09; Прочитано: 1394 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
