 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вывод уравнения колебания струны
|
|
Рассмотрим натянутую струну длины l, закрепленную на концах. В положении равновесия струна направлена вдоль оси Ox. Сила натяжения T 0, действующая на струну, предполагается значительной. Каждую точку струны длины l можно охарактеризовать значением ее абсциссы x и смещением этой точки в момент времени t.
Для упрощения задачи примем следующие предположения:
1. Будем рассматривать только поперечные колебания струны, предполагая, что движение происходит в одной плоскости, и что все точки струны движутся перпендикулярно оси Ox.
Тогда процесс колебания струны может быть описан одной скалярной функцией 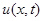 , которая характеризует (вертикальное) смещение точки струны с координатой x в момент времени t.
, которая характеризует (вертикальное) смещение точки струны с координатой x в момент времени t.
2. Будем рассматривать струну как гибкую упругую нить:
· математическое выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю. Это условие выражает собой то, что струна не сопротивляется изгибу;
· понятие "нить" означает, что мы пренебрегаем формой поперечного сечения и толщиной (рассматриваем линейную плотность ρ(x)).
3. Рассматриваем только малые колебания струны, т.е. будем считать, что смещение 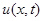 , а также
, а также 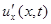 столь малы, что квадратами этих величин по сравнению с единицей можно пренебречь, т.е.
столь малы, что квадратами этих величин по сравнению с единицей можно пренебречь, т.е. 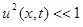 ,
, 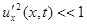 .
.
4. Величина напряжений (силы натяжения) может быть вычислена с помощью закона Гука: сила натяжения, возникающая в струне, пропорциональна ее относительному удлинению:
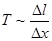 ,
,
где 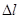 - удлинение струны;
- удлинение струны; 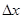 - начальная длина струны. Таким образом,
- начальная длина струны. Таким образом,
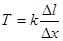 ,
,
где k – коэффициент упругости.
|
|
|
|
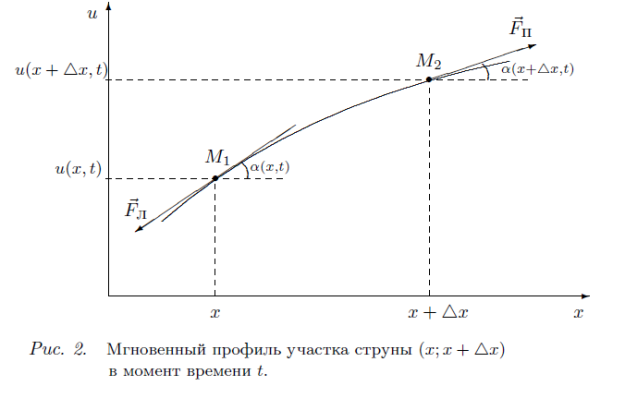
Длина произвольного участка 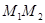 струны (рис.2.1) в любой момент времени выражается формулой:
струны (рис.2.1) в любой момент времени выражается формулой:
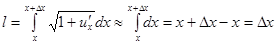 .
.
Таким образом, получаем, что при условии малых отклонений длина произвольного участка струны сохраняется. А значит, можно считать, что величина сил натяжения точек струны не изменяется с течением времени, т.е. имеем  .
.
Покажем также, что натяжение не зависит и от x. Найдем проекции натяжения на оси x и u (обозначим их Tx и Tu):
 ;
;
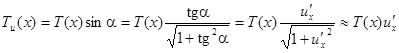 ,
,
где α – угол касательной к кривой 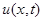 с осью x.
с осью x.
На участок 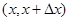 действуют силы натяжения и внешние силы. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания, т.е. струна не движется вдоль оси Ох). Так как внешние силы по предположению направлены вдоль оси u, то
действуют силы натяжения и внешние силы. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания, т.е. струна не движется вдоль оси Ох). Так как внешние силы по предположению направлены вдоль оси u, то
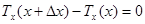 или
или 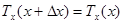 .
.
Отсюда в силу произвольности x и 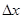 следует, что натяжение не зависит от x, т.е. для всех значений x и t:
следует, что натяжение не зависит от x, т.е. для всех значений x и t:
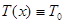 .
.
Согласно второму закону Ньютона сумма сил, действующих на участок струны 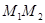 (см.рис.2.1), равна по величине и направлению вектору ускорения этого участка, умноженному на его массу. Определим величины всех сил, действующих на этот участок. Обозначим через
(см.рис.2.1), равна по величине и направлению вектору ускорения этого участка, умноженному на его массу. Определим величины всех сил, действующих на этот участок. Обозначим через 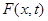 плотность распределения внешних сил, вызывающих отклонение точек струны только в вертикальном направлении. Тогда величина внешних сил, действующих на участок
плотность распределения внешних сил, вызывающих отклонение точек струны только в вертикальном направлении. Тогда величина внешних сил, действующих на участок 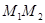 , при условии непрерывности функции
, при условии непрерывности функции 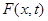 по переменной х равна:
по переменной х равна:
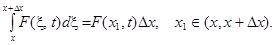
Далее, силы натяжения (левая и правая соответственно) 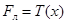 и
и 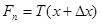 , действующие со стороны левого (в точке
, действующие со стороны левого (в точке 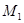 ) и правого (в точке
) и правого (в точке 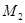 ) концов струны, направлены по касательным к мгновенному профилю струны в соответствующих точках.
) концов струны, направлены по касательным к мгновенному профилю струны в соответствующих точках.
Для вертикальной составляющей сил натяжения имеем выражение
 .
.
Так как рассматриваем малые колебания, то
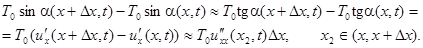
Таким образом, сумма сил, действующих на участок струны 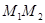 , равна:
, равна:
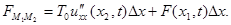 (2)
(2)
С другой стороны, рассматривая участок струны как совокупность материальных точек, имеем
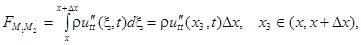 (3)
(3)
где 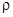 – линейная плотность струны. Приравнивая выражения (2) и (3) и переходя к пределу при
– линейная плотность струны. Приравнивая выражения (2) и (3) и переходя к пределу при 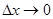 , для искомой функции получим уравнение:
, для искомой функции получим уравнение:
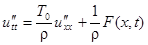
или

где 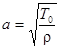 .
.
В случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны или волновое уравнение:

или
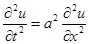 .
.
Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.
2.2. Методы решения уравнения колебания струны
2.2.1. Метод Даламбера (метод бегущих волн) для бесконечной струны
Рассмотрим свободные колебания бесконечной струны (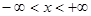 ), т.е. настолько длинной, что влиянием ее концов на процесс колебаний можно пренебречь. Причинами колебаний могут являться начальные отклонения струны от равновесного положения и (или) сообщенный струне начальный импульс, обусловливающий некоторое начальное распределение скоростей частиц струны. Эти причины описываются начальными условиями. Требуется найти профиль струны в любой момент времени.
), т.е. настолько длинной, что влиянием ее концов на процесс колебаний можно пренебречь. Причинами колебаний могут являться начальные отклонения струны от равновесного положения и (или) сообщенный струне начальный импульс, обусловливающий некоторое начальное распределение скоростей частиц струны. Эти причины описываются начальными условиями. Требуется найти профиль струны в любой момент времени.
Итак, рассмотрим задачу Коши для уравнения колебания струны:
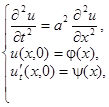 (4)
(4)
где 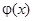 – функция, задающая форму струны в начальный момент времени;
– функция, задающая форму струны в начальный момент времени; 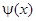 – скорость точки струны в начальный момент.
– скорость точки струны в начальный момент.
Уравнение решается в явном виде с помощью замены переменных  :
:
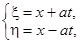
где
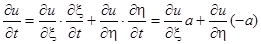 ;
;
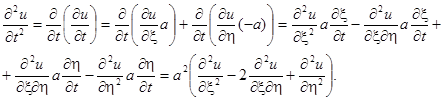
Аналогично,
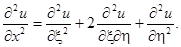
Подставляем в уравнение

Отсюда
 .
.
Интегрируя это равенство последовательно по каждой переменной, получим:
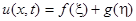 .
.
Вернемся к старым переменным:
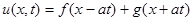 . (5)
. (5)
Функция 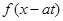 описывает волну, бегущую вправо со скоростью а, а функция
описывает волну, бегущую вправо со скоростью а, а функция 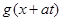 – волну, бегущую влево.
– волну, бегущую влево.
Функция (5) является общим интегралом уравнения (4). Теперь необходимо удовлетворить начальным условиям:
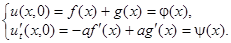
Интегрируя последнее уравнение системы, получим:
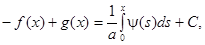
где 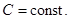
Или
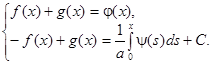
Складывая и вычитая уравнения данной системы, находим:
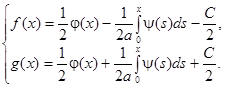
Отсюда

Подставляем эти выражения в формулу (5) и получаем решение волнового уравнения (формула Даламбера):

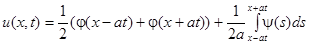 . (6)
. (6)
Рассмотрим два частных случая.
Допустим, что 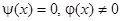 , т.е. струне придана начальная форма при нулевой начальной скорости. Тогда решение (6) принимает вид
, т.е. струне придана начальная форма при нулевой начальной скорости. Тогда решение (6) принимает вид
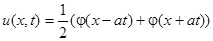
и, следовательно, представляет собой сумму двух бегущих волн: прямой волны 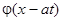 и обратной волны
и обратной волны 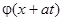 . Первая перемещается по направлению оси ОХ, а вторая – в противоположном направлении.
. Первая перемещается по направлению оси ОХ, а вторая – в противоположном направлении.
При 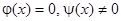 решение (6) имеет вид
решение (6) имеет вид
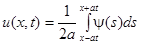 .
.
Пусть
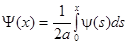 ,
,
тогда
 .
.
И в этом случае решение начальной задачи представляет собой сумму двух волн: прямой волны 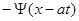 и обратной волны
и обратной волны 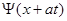 .
.
Заметим, что рассмотренная нами бесконечная струна является математической идеализацией реальных струн очень большой длины.
Пример. Решить уравнение колебания бесконечной струны 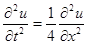 , удовлетворяющее условиям:
, удовлетворяющее условиям: 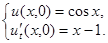
Решение: Имеем задачу свободных колебаний бесконечной струны (без краевых условий). Применяем формулу Даламбера:

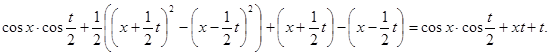
2.2.2. Фазовая плоскость
Для выявления характера решения волнового уравнения (6) удобно воспользоваться плоскостью состояний (x, t) или «фазовой плоскостью» (рис.2.2). Прямые 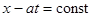 и
и 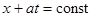 называются характеристиками уравнения (6). Функция
называются характеристиками уравнения (6). Функция 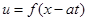 вдоль характеристики
вдоль характеристики 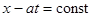 сохраняет постоянное значение, функция
сохраняет постоянное значение, функция 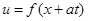 постоянна вдоль характеристики
постоянна вдоль характеристики 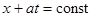 .
.
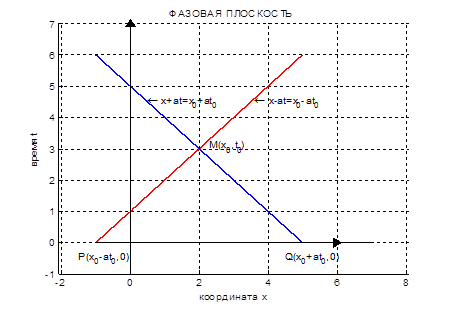
Рис.2.2. Характеристический треугольник MPQ фазовой плоскости
Рассмотрим некоторую фиксированную точку 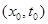 и проведем из нее обе характеристики
и проведем из нее обе характеристики 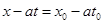 и
и 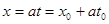 , которые пересекают ось ОX в точках
, которые пересекают ось ОX в точках 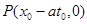 и
и 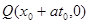 . Треугольник MPQ называется характеристическим треугольником точки
. Треугольник MPQ называется характеристическим треугольником точки 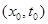 . Отклонение
. Отклонение  точки струны в момент времени
точки струны в момент времени 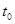 зависит только от значений начального отклонения в вершинах P и Q треугольника MPQ и от значений начальной скорости на стороне PQ:
зависит только от значений начального отклонения в вершинах P и Q треугольника MPQ и от значений начальной скорости на стороне PQ:
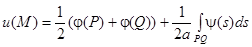 .
.
Начальные данные, заданные вне PQ, не оказывают влияния на значения 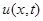 в точке
в точке  . Если начальные условия заданы не на всей бесконечной прямой, а на отрезке
. Если начальные условия заданы не на всей бесконечной прямой, а на отрезке 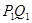 , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок
, то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок 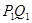 .
.
Решение можно представить в виде суммы
 где
где
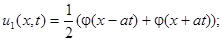
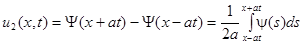 .
.
Наглядное представление о характере процесса распространения можно получить с помощью фазовой плоскости (x, t). Проведем характеристики через точки (– l, 0) и (l, 0). Они разбивают плоскость 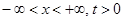 на шесть областей (рис.2.3).
на шесть областей (рис.2.3).
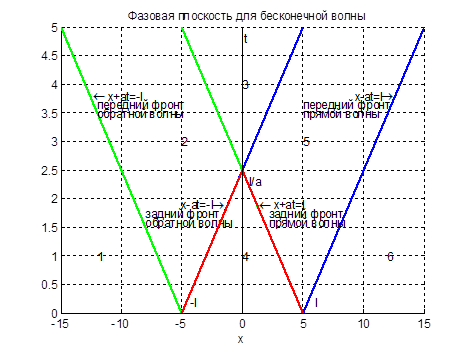
Рис.2.3. Фазовая плоскость для бесконечной волны 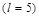
Рассмотрим два случая.
Пусть 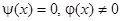 на отрезке
на отрезке 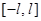 .
.
Если начальная скорость равна нулю, то отклонение 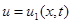 есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией
есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 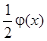 , равной половине начального отклонения.
, равной половине начального отклонения.
Области 1, 6 – колебаний нет.
Область 2: 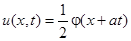 – волна движется влево.
– волна движется влево.
Область 5: 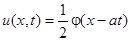 – волна движется вправо.
– волна движется вправо.
Область 4: 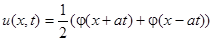 – волны складываются.
– волны складываются.
Область 3 – колебаний нет, отклонение равно нулю.
Пусть 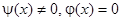 на отрезке
на отрезке 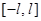 .
.
Если начальное отклонение равно нулю, то 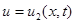 представляет возмущение струны, создаваемое начальной скоростью.
представляет возмущение струны, создаваемое начальной скоростью.
Области 1, 6: колебаний и отклонений нет.
Область 2: 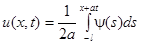 – волна бежит влево с изменением формы.
– волна бежит влево с изменением формы.
Область 5: 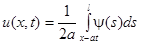 – волна бежит вправо с изменением формы.
– волна бежит вправо с изменением формы.
Область 4: 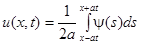 – волны складываются.
– волны складываются.
Область 3: 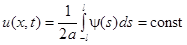 – колебаний нет, но струна не возвращается в исходное положение (если постоянная не равна нулю).
– колебаний нет, но струна не возвращается в исходное положение (если постоянная не равна нулю).
Пример. Построить профиль струны при  для различных моментов времени в случае
для различных моментов времени в случае 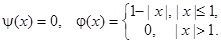
В этом случае прямая волна 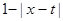 движется вправо, а обратная
движется вправо, а обратная 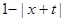 – влево (рис.2.4).
– влево (рис.2.4).
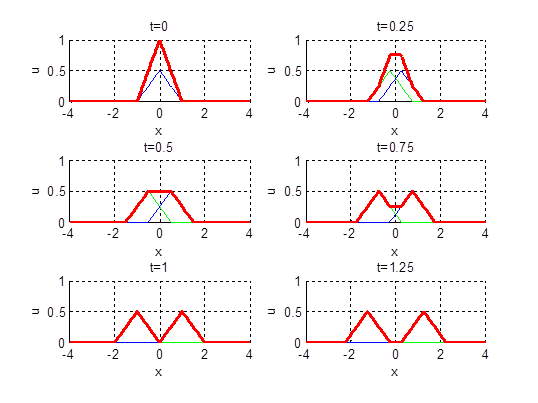
Рис. 2.4. Профили струны для различных моментов времени в случае нулевой начальной скорости
Пример. Построить профиль струны для различных моментов времени в случае 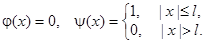
Найдем выражение для 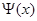 :
:
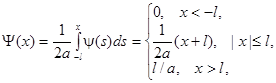 так как в силу непрерывности при
так как в силу непрерывности при 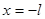 :
: 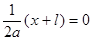 , а при
, а при 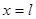 :
: 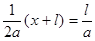 .
.
В этом случае прямая волна 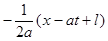 движется вправо, а обратная
движется вправо, а обратная 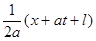 – влево (рис.2.5).
– влево (рис.2.5).
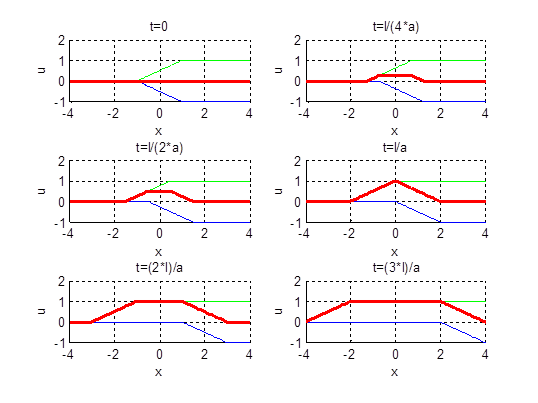
Рис.2.5. Профили струны для различных моментов времени в случае нулевого начального отклонения
График изменения профиля струны с течением времени, например, для случая 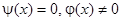 можно продемонстрировать в среде MATLAB:
можно продемонстрировать в среде MATLAB:
a=1;
l=1;
dx=.01;
x=-4*l:dx:4*l;
u=1-abs(x);
u(abs(x)>l)=0;
u_left=.5*u;
u_right=.5*u;
for t=0:.25:1.25
subplot(3,2,4*t+1);
hold on
u1=circshift(u_left,[0 -a*t/dx]);
u2=circshift(u_right,[0 a*t/dx]);
plot(x,u1,'g-','lineWidth',2);
plot(x,u2,'b-','lineWidth',2);
plot(x,u1+u2,'r-','lineWidth',3);
xlim([-4*l 4*l]);
ylim([0 1]);
grid on
xlabel('x');
ylabel('u');
title(['t=' num2str(t)]);
end
2.2.3. Метод продолжений для полубесконечной струны
Рассмотрим задачу о распространении волн на полубесконечной прямой, (x ≥ 0). Следует отметить, что чаще всего имеют дело с жестким или свободным закреплением струны.
При анализе этих задач нам понадобятся леммы о свойствах решений уравнений колебаний, определенных на бесконечной прямой.
Лемма 1. Если начальные данные в задаче о распространении колебаний на неограниченной прямой являются нечетными функциями относительно некоторой точки 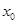 , то соответствующее решение в этой точке равно нулю:
, то соответствующее решение в этой точке равно нулю:  .
.
Доказательство леммы 1.
Примем 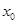 за начало координат,
за начало координат, 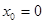 . В этом случае условия нечетности начальных данных запишутся в виде
. В этом случае условия нечетности начальных данных запишутся в виде
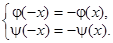
Функция 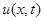 при
при  равна
равна
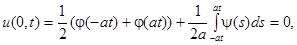
так как первое слагаемое равно нулю в силу нечетности 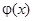 , а второе равно нулю, поскольку интеграл от нечетной функции в пределах, симметричных относительно начала координат, всегда равен нулю.
, а второе равно нулю, поскольку интеграл от нечетной функции в пределах, симметричных относительно начала координат, всегда равен нулю.
Лемма 2. Если начальные данные в задаче о распространении колебаний на неограниченной прямой являются четными функциями относительно некоторой точки 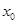 , то производная по x соответствующего решения в этой точке равна нулю:
, то производная по x соответствующего решения в этой точке равна нулю: 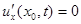 .
.
Доказательство леммы 2.
Условие четности начальных данных имеет вид:
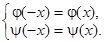
Заметим, что производная четной функции является функцией нечетной: 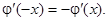 Рассмотрим производную:
Рассмотрим производную:
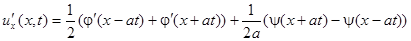 ;
;
 .
.
Так как первое слагаемое равно нулю в силу нечетности 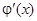 , а второе – в силу четности
, а второе – в силу четности 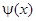 .
.
Дата публикования: 2015-10-09; Прочитано: 3436 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

 в момент времени t
в момент времени t