Упражнения. Найти общее решение следующих дифференциальных уравнений с частными производными

Найти общее решение 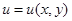следующих дифференциальных уравнений с частными производными. Выполнить проверку.

1.1. .

Ответ: .

1.2. .

Ответ: .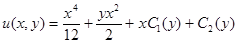

1.3. .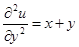

Ответ: .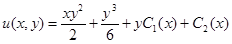

1.4. .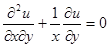

Ответ: .

1.5. .

Ответ: .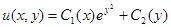

1.6. .

Ответ: .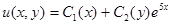

1.7. .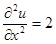

Ответ: .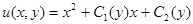

1.8. .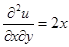

Ответ: .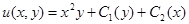

1.9. .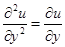

Ответ: .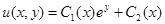

1.10. .

Ответ: .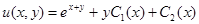

1.11. .

Ответ: .

1.12. .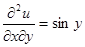

Ответ: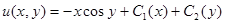

Начальные и граничные условия

Задача Коши для дифференциальных уравнений первого порядка

Будем рассматривать случай, когда искомая функция 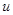зависит от двух переменных . Тогда уравнение 1-го порядка будет иметь вид

.

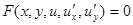Всякое решение данного уравнения будем называть интегральной поверхностью (график решения – поверхность в пространстве с координатами ).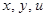

Для того чтобы из совокупности всех решений данного уравнения выделить некоторое частное решение, формулируется задача Коши: найти решение уравнения 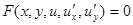, удовлетворяющее условию 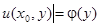, где 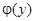– некоторая заданная функция.

Обозначим через l кривую в пространстве 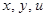, задаваемую уравнениями: .

Тогда задача Коши имеет следующий геометрический смысл: среди всех интегральных поверхностей найти ту, которая проходит через заданную кривую l.

1.2.2. Задача Коши для дифференциальных уравнений второго порядка

Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Для того чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за 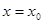. В результате возникает задача Коши:

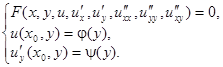
Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, т.е. уравнений, описывающих нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.

Для волнового уравнения 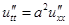задаются два начальных условия: 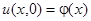и 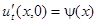. Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие – начальные скорости точек струны. В случае волнового уравнения 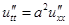на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ, соответственно, будут зависеть от двух или трех переменных.

Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными или краевыми условиями. Если в задаче заданы начальные и граничные условия, то такая задача называется смешанной.

Для уравнения колебаний струны часто задаются условия: . Эти условия физически означают, что концы струны закреплены (т.е. отклонения 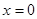при и при 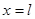в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, – свободные концы струны.