Численные методы решения дифференциальных уравнений в частных производных

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных

Одним из наиболее распространенных численных методов решения уравнений в частных производных является метод сеток. В методе сеток область Ω, в которой необходимо найти решение уравнения, разобьем прямыми, параллельными осям 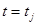и , на прямоугольные области (рис.1.1), где , 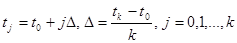. Точки, которые лежат на границе области Ω, называются внешними, остальные точки – внутренними. Совокупность всех точек называется сеткой, величины h и Δ шагами сетки по х и t соответственно.

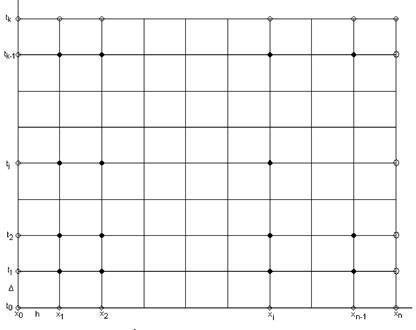
Рис.1.1. Сетка 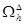для области Ω

Идея метода сеток состоит в том, что вместо любой непрерывной функции 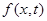будем рассматривать дискретную функцию , которая определена в узлах сетки 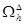, вместо производных функции будем рассматривать их простейшие разностные аппроксимации в узлах сетки. Таким образом, вместо системы дифференциальных уравнений в частных производных получим систему алгебраических уравнений. Чем меньше величины h иΔ, тем точнее получаемые алгебраические уравнения моделируют исходное дифференциальное уравнение в частных производных. В этом и последующих подразделах этой главы будет рассмотрен метод сеток для каждого из трех типов уравнений и его реализация в MATLAB. Знакомство с численными методами решения дифференциальных уравнений в частных производных начнем с разностных схем решения параболических уравнений.

Разностные схемы решения параболических уравнений будем рассматривать на примере следующего одномерного уравнения:

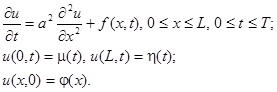
Построим сетку 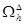(см. рис.1.1). Для получения сеточного уравнения заменим производную 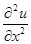приближенной разностной формулой:

.

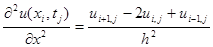В этой и последующих формулах 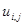– значение функции u в точке 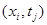, 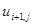– в точке 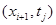, 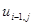– в точке 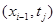, 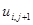– в точке 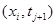, 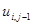– в точке .

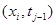Для замены 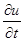можно воспользоваться одной из приближенных разностных формул

;

.

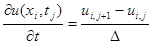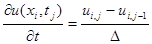Кроме того, заменим начальные и граничные условия их разностной аппроксимацией:

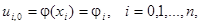
Заменив частные производные в задаче соответствующими разностными соотношениями, получим следующую вычислительную схему для расчета значений функции и в узлах сетки :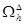

,

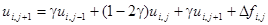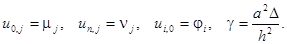
Это явная двухслойная разностная схема (рис.1.2).

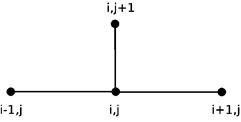
Рис.1.2. Шаблон явной двухслойной разностной схемы

Учитывая, что на нулевом слое (при i = 0) все значения 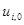(как, впрочем, и 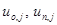) известны, можно сначала явно рассчитать значения 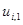, затем 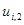и так до . Для устойчивости разностной схемы значения шагов по t и х должны удовлетворять следующему условию:

.

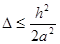Пример. Решить параболическое уравнение, описывающее распределение температуры в стержне длиной L, начальная температура стержня задается произвольной функцией 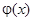. Температуры концов стержня равны .

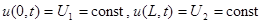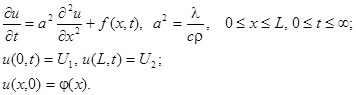
Здесь а ² – коэффициент температуропроводности, 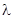– коэффициент теплопроводности материала стержня, с – удельная теплоемкость, 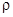– плотность массы.

Подпрограмма решения задачи с помощью явной разностной схемы в MATLAB:

//Правая часть дифференциального уравнения

function y=f(x,t)

y=sin(x*t)

endfunction

//Начальное условие

function y=fi(x)

y=exp(0.15*x)

endfunction

//Условие на левой границе

function y=myu(t)

y=l

endfunction

//Условие на правой границе

function y=nyu(x)

y=2.117

endfunction

function [u,x,t]=parabol(N,K,L,T,a)

//Функция решения параболического уравнения методом сеток с

//помощью явной разностной схемы. N - количество участков разбиения интервала по х (0,1_); К – количество участков разбиения интервала по t (0,Т); а - коэффициент температуропроводности,

// Функция возвращает матрицу решений u вектора х, t

// Вычисляем шаг по х

H = L/N;

// Вычисляем шаг по t

Delta = T/K;

// Формируем массив х и первый столбец матрицы решений u

// из начального условия

for I = l:N+l

x(i) = (i-l)*h;

u(i,l) = fi(x(i));

end

//Формируем массив t, первую и последнюю строку матрицы решений u из граничных условий

for j = l:K+l

t(j) = (j-l)*delta;

u(l,j) = myu(t(j));

u(N+l,j) = nyu(t(j));

end

gam = a^{^}2*delta/h^{^}2;

// Формируем матрицу решений u

for j = l:K

for i = 2:N

u(i,j+l) = gam*u(i-l,j)+(l-2*gam)*u(i,j)+gam*u(i+l,j)+delta*...

f(x(i),t(j));

end

end

end

Входными данными подпрограммы parabol решения задачи являются: N – количество интервалов, на которые разбивается отрезок (О, L); К – количество интервалов, на которые разбивается отрезок (О, Т); L – длина стержня, Т – интервал времени, а – параметр дифференциального уравнения. Функция возвращает три параметра: решение – сеточная функция u, определенная на сетке 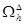, массивы x и t.

[U,Х,T]=parabol(50,200,5,3,0.4);

surf(X,T,U');

xlabel('X');

ylabel('T');

График решения данной задачи изображен на рис.1.3.

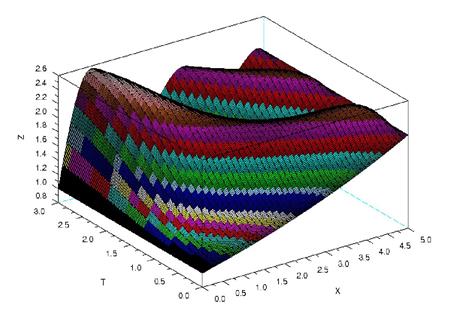
Рис.1.3. График решения параболического уравнения при