Понятие об общем решении уравнения в частных производных

Рассмотрим обыкновенное дифференциальное уравнение n -го порядка: 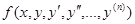. Его общий интеграл представляет собой некоторое семейство функций, зависящее от n произвольных постоянных . Любое частное решение получается из него, если параметрам 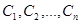придать определенные значения.

Рассмотрим решения некоторых дифференциальных уравнений в частных производных.

Пример 1. Пусть дано уравнени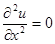е , где .

Решение. Найдем его общий интеграл, т.е. функцию 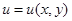, удовлетворяющую данному уравнению. Сначала запишем это уравнение в виде: 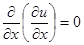. Поскольку производная по переменной х от величины, стоящей в скобках, равна нулю, то последняя является некоторой произвольной функцией от у: 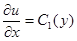. Поэтому . Интегрируя произвольную функцию 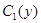, получили функцию 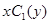плюс произвольная функция . Таким образом, общий интеграл уравнения 2-го порядка содержит две произвольные функции.

Пример 2. Решить уравнени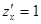е , где .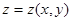

Решение. Проинтегрируем обе части уравнения по х:

,

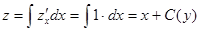где 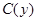– произвольная функция.

Пример 3. Решить уравнени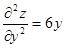е , где .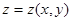

Решение. Проинтегрируем обе части уравнения по у:

,

где 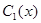– произвольная функция.

Интегрируем повторно по у полученное равенство:

,

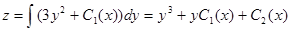где 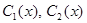– произвольные функции.

Пример 4. Решить уравнени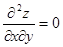е , где .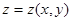

Решение. Проинтегрируем обе части уравнения сначала по х, а затем по у:

,

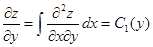тогда

,

где 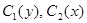– произвольные функции.

Замечание. В отличие от общего решения обыкновенного дифференциального уравнения, зависящего от произвольных постоянных, общее решение уравнения с частными производными зависит от произвольных функций, количество которых равно порядку уравнения.