 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление определенных интегралов численными методами
|
|
Определенный интеграл от непрерывной функции f (х) ³ 0 в пределах от а до b представляет площадь криволинейной трапеции S, ограниченной кривой f (x), осью абсцисс и прямыми х = а, х = b (рисунок 18). Из курса высшей математики известно, что
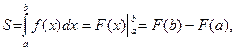
где F (x) – первообразная для f (х) на отрезке [ а, b ], т. е.. F ¢ (x) = f (х) на отрезке [a, b]. Если f (х) <0 на отрезке [a, b], то в формуле S < 0, но ç S çравно площади криволинейной трапеции, находящейся под осью абсцисс.
 y
y
y = f (x)
S
0 a bx
|
Однако на практике приведённой формулой часто нельзя воспользоваться по двум основным причинам:
1) вид функции f (x) не допускает непосредственного интегрирования, т. е. первообразную нельзя выразить в элементарных функциях;
2) значения функции f (x) заданы только на фиксированном конечном множестве точек xi, т. е. функция задана в виде таблицы.
В этих случаях используются методы численного интегрирования. Они основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например, многочленами нулевой (у = с), первой
(у = сх + d) или второй (у = сx 2 + dх + k) степени, а численные методы вычисления определенного интеграла, основанные на подобной аппроксимации, называются соответственно методами прямоугольников, трапеций и Симпсона (парабол).
Пусть требуется приближенно вычислить значение интеграла 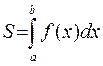 В методе прямоугольников (рисунок 19) криволинейная трапеция разбивается на п частей, каждая из которых представляет собой прямоугольник, основание которого равно шагу интегрирования
В методе прямоугольников (рисунок 19) криволинейная трапеция разбивается на п частей, каждая из которых представляет собой прямоугольник, основание которого равно шагу интегрирования 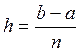 , а длины сторон соответственно Y 0 = f (x 0), Y 1 = f (x 1), Yn = f (xn), где x 0 = a, x 1, …, xn-1, xn = b – точки деления отрезка [ a, b ] на n равных частей.
, а длины сторон соответственно Y 0 = f (x 0), Y 1 = f (x 1), Yn = f (xn), где x 0 = a, x 1, …, xn-1, xn = b – точки деления отрезка [ a, b ] на n равных частей.
Различают методы правых, левых и средних прямоугольников, в зависимости от месторасположения начальной точки x 0 при вычислении площади элементарного прямоугольника. При этом если за высоту каждого прямоугольника принимается левая ордината (y 0, y 1, y 2…), то вычисление интеграла будет производиться по методу левых прямоугольников; если правая ордината (y 1, y 2, y 3…), то по методу правых прямоугольников; если за высоту принимается середина интервала h, то будет применяться метод средних прямоугольников. Основанием всех прямоугольников будет являться величина шага интегрирования h.
  у у
 Уn¢ Уn Уn¢ Уn

У = f(x) У'2
S1 S2
0 X0 = а X1 X2 Xn-1 Xn = b х Рисунок 19 К выводу формул вычисления определённых интегралов |
Тогда при методе левых прямоугольников
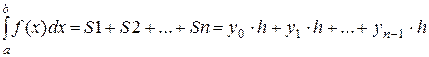 ,
,
при методе правых
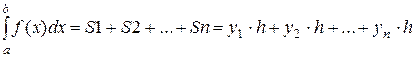 ,
,
при методе средних
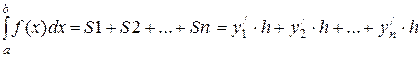 .
.
Как видно из рисунка 19 первоначальное значение  при методе левых прямоугольников
при методе левых прямоугольников  , правых –
, правых – 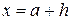 , средних
, средних 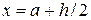 . Последующие значения
. Последующие значения 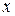 будут получаться через операцию присваивание
будут получаться через операцию присваивание 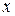 =
= 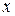 + h, а элементарные площади S 1, S 2,… Sn будут вычисляться по формуле
+ h, а элементарные площади S 1, S 2,… Sn будут вычисляться по формуле 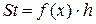 . Сумма этих площадей дает значение интеграла. Изложенное выше реализует алгоритм (рисунок 20), где
. Сумма этих площадей дает значение интеграла. Изложенное выше реализует алгоритм (рисунок 20), где 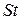 - значения элементарных площадей, а их сумма S – значение интеграла.
- значения элементарных площадей, а их сумма S – значение интеграла.
 5 8
6 9
Рисунок 20 Схема алгоритма вычисления интеграла методом прямоугольников
5 8
6 9
Рисунок 20 Схема алгоритма вычисления интеграла методом прямоугольников
|
Более точное значение интеграла получается при вычислении его методом трапеций, когда ординаты (y 0, y 1, y 2… yn) подынтегральной функции соединяют отрезками прямых и искомую площадь заменяют суммой площадей трапеций, высотой которых является шаг h, а основаниями 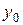 и
и 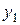 для S 1,
для S 1, 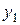 и
и  для S 2 (рисунок 19).
для S 2 (рисунок 19).
Тогда
 ,
,
где 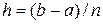 , а y 0, y 1, y 2 … yn равны значениям функции
, а y 0, y 1, y 2 … yn равны значениям функции 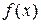 при соответствующих значениях аргумента
при соответствующих значениях аргумента 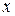 .
.
Поскольку 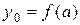 ,
, 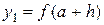 ,
, 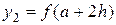 …, то схема алгоритма примет вид, приведенный на рисунке 21. В приведенном алгоритме блок 5 вычисляет значение элементарных площадей S 1, S 2,… Sn, в блоке 6 осуществляется их суммирование и блоком 7 изменяется
…, то схема алгоритма примет вид, приведенный на рисунке 21. В приведенном алгоритме блок 5 вычисляет значение элементарных площадей S 1, S 2,… Sn, в блоке 6 осуществляется их суммирование и блоком 7 изменяется 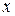 на величину шага h.
на величину шага h.
 1
Рисунок 21 Схема алгоритма вычисления интеграла методом трапеций 1
Рисунок 21 Схема алгоритма вычисления интеграла методом трапеций
|
Программа вычисления 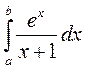 методом трапеций, согласно приведённому алгоритму имеет вид.
методом трапеций, согласно приведённому алгоритму имеет вид.
Дата публикования: 2015-10-09; Прочитано: 249 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!




 h h
h h