Методические указания к выполнению задания 2

При решении любое нелинейное уравнение, например , предварительно приводится к виду 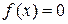, т. е. 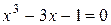, при этом функции 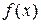могут быть алгебраическими, у которых над аргументом х выполняются лишь арифметические операции, и трансцендентными, которые содержат, кроме того, показательные, логарифмические, тригонометрические функции аргумента х. Такие уравнения далеко не всегда можно решить точно, а для практических расчётов точное решение не всегда является обязательным.
Поэтому особое значение с развитием вычислительной техники приобрели способы приближённого вычисления корней и оценки их точности.

Данная процедура состоит из двух этапов: 1) отделение корней, т. е.. выделение таких отрезков [ a, b ], в каждом из которых находится только один корень уравнения или нахождение первоначальных приближений корней;
2) уточнение корней, т. е.. нахождение их на найденных отрезках с заданной степенью точности.

1. Простейшим способом отделения корней является графический. На графике функции 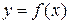определяются отрезки [ a, b ], в пределах которых лежат точки пересечения функции с осью 0х, являющимися приближенными значениями корней. Например, при решении уравнения 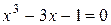сначала вычисляем значения функции 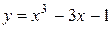, по заданным значениям аргумента х (таблица 6) и затем по полученным данным строим график (рисунок 12).

Таблица 6

Результаты табулирования функции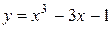

х –3 –2 –1           y –19 –3   –1 –3       У -3 -2 -1 0 1 2 3 х -1 -2 -3 Рисунок 12 График функции

Как видно из графика, уравнение имеет 3 корня на отрезках [–2, –1],

[–1,0] и [1,2].

Отделить корни можно также программным способом. Для составления алгоритма решения данной задачи рассмотрим поведение функции 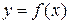на интервале от х _нач до х _кон с шагом h (рисунок 13)

у

F

х _нач С х _кон

h A h В 0 х

D

у

у 1

Рисунок 13 График функции 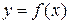при наличии корней

Как видно из рисунка, корни уравнения находятся в точках А, В и С, где 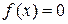. Данные точки можно обнаружить, рассчитывая значения функции 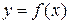от х _нач до х _кон с шагом h и наблюдая за изменением её знака. Так, в точке А значение функции изменяется с «-» на «+», а в точке В с «+» на «-» и т. д. Обнаружить изменение знака функции можно путём перемножения двух её значений, вычисленных от аргументов х, находящихся в соседних точках на расстоянии h одно от другого. Для точки А, например, это будут значения функции D и F.

Отделение корней по рассмотренному методу реализует алгоритм, представленный на рисунке 14.

1           4   11 нет да 6 12 нет 13 8 да 9 14 Рисунок 14 Схема алгоритм отделения корней функции f(x) на отрезке [ х нач, х кон].

В блоке 2 вводятся начальное значение аргумента функции х _нач, конечное х _кон и шаг его изменения h.

В блоке 3 принимается текущее значение х за х _нач и количество корней

m = 0, а в блоке 4 вычисляется первоначальное значение функции у 1 при х = х _нач.

Блок 5 организует цикл по изменению х от х + h до х _кон с шагом h. В блоке 6 вычисляется очередное значение функции в точке 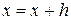(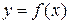). Затем в блоке 7 проверяется, не пересекла ли функция 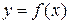ось ОХ. В случае отсутствия пересечения 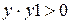полученное значение у в блоке 10 запоминается как у ₁, а в блоке 5 значение х опять изменяется на величину шага h. Затем в блоке 6 снова вычисляется у и в блоке 7 проверяется функция на изменение знака. Так как в этом случае 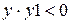(точки D и F на рисунок 4), то в блоке 8 выводятся значения аргумента х - h и x, в пределах которых находится корень уравнения, а в блоке 9 фиксируется увеличение количества найденных корней на единицу. Циклический процесс повторяется до принятого конечного значения аргумента х _кон. В результате будут найдены отрезки, на которых находятся корни нелинейного уравнения (около точек А, В, С на рисунок 13).

Программа на языке Basic, реализующая данный алгоритм для уравнения , будет следующей:

PRINT ² Введите X_нач, X_кон, H ²

INPUT XN, XK, H

X = XN: M = 0

Y1 = X*X*X- 3*X - 1

FOR X = X + H TO XK STEP H

Y = X*X*X - 3*X - 1

IF Y*Y1 < 0 THEN GOTO 2 ELSE GOTO 5

2 PRINT “A=”; X - H; “B=”; X

M = M + 1

5 Y1= Y

NEXT X

IF M = 0 THEN PRINT “корней нет” ELSE PRINT “корней=”;M

END

Уточнение корня, найденного на отрезке [а, b], осуществляется одним из следующих методов: деления отрезка пополам, хорд (секущих), касательных (Ньютона), итераций. Рассмотрим некоторые из них, например, метод деления отрезка пополам (рисунок 15). Интервал [а, b] делится пополам и в найденной точке (с = (a + b) / 2) вычисляется значение функции y = f (с). Если ê y ê£ е, где е – заданная точность, то C является корнем уравнения, т.к. при полученном C функция y = f (C) меньше точности е. В противном случае выбираем один из отрезков - или [ а, (а + b) / 2] (рисунок 15 а), или [(а + b) / 2, b ] (рисунок 15 б), на концах которого f (x) имеет противоположные знаки.
Выбранный интервал снова делим пополам (с = (a + b) / 2) и вычисляем значение функции y = f (с). Процесс повторяется до тех пор, пока не будет получено значение ç y ê£ е.

у у = f(x)   у   0 а b х   у 1 а)	у у = f(x)       a b х y у 1 б)
Рисунок 15 Уточнение корня методом деления отрезка пополам

Сказанное выше реализуется следующим алгоритмом (рисунок 16), где в блоке 2 вводятся полученные при отделении корней границы интервала [ а, b ] и точность вычисления корня е, а в блоке 3 вычисляется значения функции у ₁ при х = а. Затем в блоке 4 вычисляется середина интервала [ а, b ], а в блоке 5 – значение функции в середине данного интервала при
с = (a + b) /2. Если при проверке в блоке 6 оказывается ç y ê£ е, то с – корень уравнения, который выводится в блоке 10. Если же условие ç y ê£ е не выполняется, то в блоке 7 определяется: какую половину отрезка [ а, b ] оставить для дальнейшего нахождения корня. Если 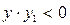, то левую присвоением b = с (блок 9), а если же нет, то правую присвоением a = с (блок 8) и затем в блоке 4 опять определяется середина нового суженного интервала и процесс повторяется до тех пор, пока значение у станет меньше заданной точности е.

1   2                 6 да   нет нет 7 да 8 9     Рисунок 16 Схема алгоритма уточнения корня методом деления отрезка пополам

Программа на языке Basic, реализующая данный алгоритм для уравнения , будет следующей:

PRINT “Введите A, B, E “