О теории параллельных линий

О ТЕОРИИ ПАРАЛЛЕЛЬНЫХ ЛИНИЙ

Cодержание:

Предисловие 3

О теории параллельных линий 6

Заключение 15

Пояснения 21

Литература 46

Предисловие

При попытке понять геометрию как науку у многих могут возникать некоторые сложности о решении которых мне бы хотелось сказать и на которых остановиться. С древних времён Геометрия была наукой о пространстве и её истины устанавливались с абсолютной достоверностью и на вечные времена. Сложности же о которых я хочу сказать возникли тогда, когда были открыты неевклидовы геометрии.[1] Часто приходится слышать и читать, что в геометрии как науке произошёл некоторый переворот, и многие ранее несомненные истины оказались на самом деле нашими предубеждениями или чем то вроде привычки. Так, например, аксиома о том, что через точку (A) не лежащую на некоторой прямой (a)

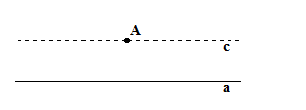
проходит только одна прямая (c), такая что она не пересекает (a) и не более – это не несомненная аксиома, а лишь один из одинаково возможных вариантов – этого, и ещё двух, – что через точку (А) проходят бесконечно много прямых не пересекающих прямую (а), и что через неё не проходит не одной такой прямой.

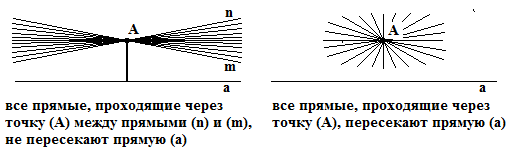
Здесь я бы хотел постараться разобраться как это всё можно понять (что здесь имеется ввиду) и действительно ли имеет место такой переворот в Геометрии. А точнее постараться обосновать ту точку зрения – что такого переворота нет. Рассмотрим в таком случае два основных подхода, которые используются для понимания и объяснения неевклидовых геометрий. Первый подход к пониманию неевклидовых геометрий будем называть формальным подходом[2]. Он состоит в том, что прямыми, плоскостями и точками, мы можем называть не обязательно действительные прямые, плоскости и точки как мы их мыслим себе в своём воображении, но и любые другие объекты между которыми выполняются отношения задаваемые тем или другим набором аксиом. Так, например, прямой может называться линия идущая по поверхности шара и соединяющая две её точки кратчайшим (по поверхности) путём[3]. Понятно, что в таких геометриях (например, в сферической) некоторые теоремы Евклидовой геометрии не выполняются. Но свидетельствует ли это о каком то перевороте в Геометрии? Надо полагать, что нет. Ведь для прямых, плоскостей и точек в их первоначальном смысле, все теоремы Евклидовой геометрии так и остаются незыблемыми истинами. (формальный подход просто абстрагируется от того что конкретно мы называем прямыми, плоскостями и точками и рассматривает лишь логические отношения между ними)[4]

Рассмотрим теперь второй более сложный подход к истолкованию неевклидовых геометрий о котором и будем говорить. Хотелось бы назвать этот подход – подходом Гаусса – Лобачевского.[5] Когда Н. И. Лобачевский

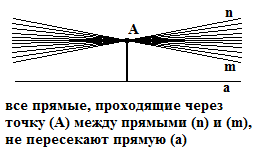
говорит что через точку (А) не лежащую на прямой (a) может проходить бесконечно много прямых не пересекающих прямую (а), он не имеет ввиду вкладывать в понятие прямой какого то нового смысла и называть прямыми – например, полуокружности на плоскости или какие – нибудь вообще не имеющие – пространственно представляемых образов логические объекты. Именно для прямых (тех самых настоящих прямых) Лобачевский ставит вопрос – а обязательно ли всегда должна выполняться аксиома о параллельных (приведённая аксиома) и отвечает на него, что наш разум способен допустить и пространство в котором она выполняется (Евклидово пространство), и пространство в котором она замена аксиомой с бесконечным числом непересекающих прямых (пространство Лобачевского – его ВООБРАЖАЕМАЯ ГЕОМЕТРИЯ). При этом Лобачевский стоит на более классических позициях чем сторонники формального подхода – в том смысле, что все остальные аксиомы Геометрии, кроме аксиомы о параллельных – являются для него абсолютными и несомненными геометрическими истинами. То есть по Лобачевскому все остальные аксиомы геометрии – происходят из наших понятий о пространстве (у Лобачевского – о телах[6]) и лишь аксиома о параллельных нам как бы не абсолютно очевидна – то что она может быть не выполняется в окружающем нас пространстве, по Лобачевскому – требует экспериментальной проверки. [7]

Автор этой статьи постарается показать, что и этот подход не может нас убедить в том, что произошёл переворот в геометрии – сопровождающийся упразднением каких либо геометрических истин (таких например как теорема Пифагора)[8]. (причём показать чисто математически – в том смысле, чтобы не поднимать при этом вопрос о действительном существовании или не существовании неевклидовых пространств а также о возможности или не возможности их представлять – не поднимать этот вопрос в том смысле, чтобы дать обоснование названной точке зрения независимое от действительного положения дел по этому вопросу)

Также мне бы хотелось (и это для меня очень важно) чтобы моя работа была ещё и введением в основания Геометрии – чтобы она могла помочь Вам, даже если Вы ещё совсем не разбираетесь в Геометрии, – понять некоторые основные моменты, увидеть как ведутся доказательства и начать самостоятельно ориентироваться в геометрической науке – самому уже определять, – доказательства каких теорем Вам бы было интересно узнать и также, уже, если можно так выразиться, – без страха, мочь приступать к чтению трудов великих геометров прошлого.

О теории параллельных линий

Здесь я не хотел бы пока подробно рассматривать вопрос о том, как именно и откуда наш разум заимствует геометрические аксиомы – так как в этом для меня ещё много неясного. Пока же ограничимся чисто математическим исследованием.

К некоторым геометрическим понятиям я сделаю пояснения со сноской в квадратных скобках [ ].

Сначала проясним ту роль, которую одиннадцатая аксиома[9] (пятый постулат) играет в теории Евклида. Из неё можно доказать (и обратно) следующую теорему[10]: две параллельные [см. пояснение 1 «Параллельные прямые»] прямые, если и пересекаются некоторой третьей прямой,

то пересекаются ею под одинаковыми углами (как показано на следующем рисунке – то есть одинаковыми – внешним и внутренним с одной стороны) [см. пояснение 2 «Введение в теорию параллельных»]

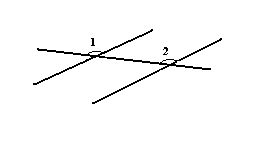
Эта теорема играет очень важную роль в теории параллельных – она служит для узнавания углов пересечения прямых. Так, например, если у нас есть две прямые проведённые к некоторой под одинаковыми углами (следующий рисунок)

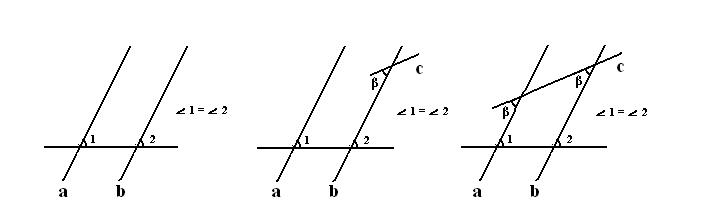
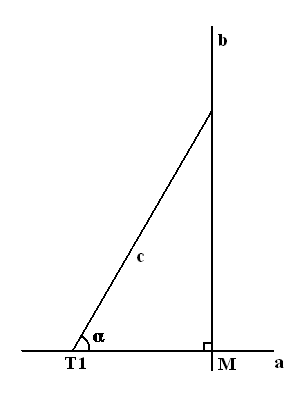
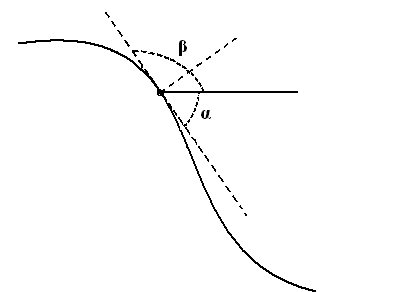
то мы знаем что они параллельны. [см. пояснение 3 «Доказателство Прокла»] Пусть теперь прямую (b) пересекает ещё и прямая (c) под углом β (второй рисунок). Благодаря установленной теореме, мы знаем, что прямая (c), продолжаясь, и прямую (a) пересечёт под тем же углом β (третий рисунок). (То, что прямая (c) пересечёт прямую (a) следует из одиннадцатой аксиомы)[11] Или, например, такой случай: пусть прямые (a) и (b) пересекаются с некоторой (d) под разными, известными нам углами α и β.

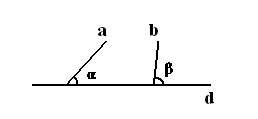
Тогда, согласно одиннадцатой аксиоме, продолжаясь они пересекутся и между собой – и пусть угол α меньше угла β (тогда прямые, продолжаясь, пересекутся со стороны углов α и β, а не с противоположной – то есть так, как показано на следующем рисунке)

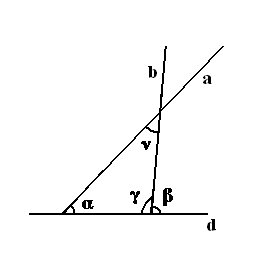
А так как сумма углов получившегося треугольника (как и любого) нам известна и равна π[12], то найдём внутренний угол пересечения прямых ν (далее просто угол пересечения прямых по продолжении) вычитая из π (суммы углов треугольника) углы α и γ.

ν = ∑△ – α – γ = π – α – γ = 2∟– α – γ (∑△ – сумма углов треугольника)

Значит благодаря тому, что сумма углов всех прямолинейных треугольников одинакова[13] и равна π, в Евклидовой геометрии – угол пересечения прямых (a и b) – по продолжении – (угол ν) – определяется только углами их (прямых a и b) пересечения с прямой (d) – углами α и γ и выражается через них.

Значит угол пересечения прямых (пересекающих некоторую) между собой – полностью определяется их углами пересечения с некоторой.

Рассмотрим теперь, выполняется ли аналогичный закон в геометрии Лобачевского. Пусть к некоторой «линии» (a) в точке M построен перпендикуляр (b), а в точке T1 – «линия» (c) под углом α – как показано на рисунке. (И пусть по продолжении «линия» (c) пересекает (b).)

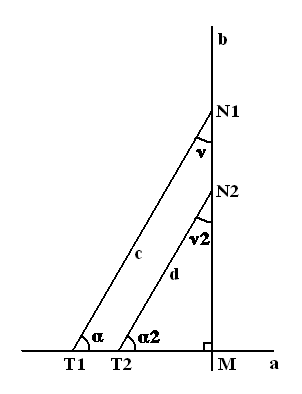
И пусть теперь из точки T2 будет под углом α2 = α построена «линия» (d) и продолжена до пересечения[14] с «линией» (b). Выполняя подобное построение в геометрии Евклида мы всегда будем иметь угол ν2 равным ν [15] – независимо от положения точки T2 на прямой (a) – и это и есть, если можно так сказать Евклидовость пространства[16]. В геометрии же Лобачевского углы ν и ν2 не будут равны. Это видно из следующего – во первых, угол ν2 будет меньше чем он был бы в геометрии Евклида. Так, пусть сумма углов треугольника (T2 M N2) будет меньше двух прямых на величину ε1. Эта величина в геометрии Лобачевского называется дефектом треугольника. Значит ∑△(T2 M N2) = 2∟ – ε1, а угол ν2 = ∑△(T2 M N2) – ∟ – α2 = 2∟ – ε1 – ∟ – α2 = ∟ – α2 – ε1. (В Евклидовой геометрии он был бы равен 2∟ – ∟ – α2 = ∟ – α2) – Значит он (угол ν2) меньше своего значения, которое он имел бы в геометрии Евклида как раз на дефект треугольника (T2 M N2). Докажем теперь одну важную теорему: если некоторый треугольник разбит на два других треугольника (как на рисунке) то его дефект равен сумме дефектов этих треугольников. [17]

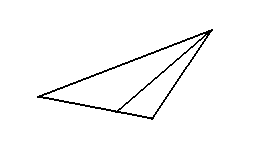
Это ясно из следующего:

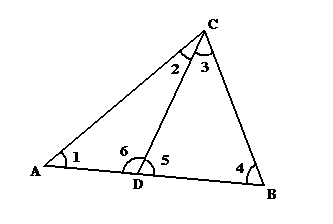
из рисунка видно, что суммы углов треугольников ADC и DBC → (∠1 + ∠2 + ∠6) и (∠3 + ∠4 + ∠5) вместе, (но если из них, вычесть углы 6 и 5) составляют сумму углов треугольника ABC → (∠1 + ∠2 + ∠3 + ∠4) то есть справедливо соотношение ∑△ADC + ∑△DBC – ∠5 – ∠6 = ∑△ABC. Но углы 5 и 6 вместе составляют два прямых (примем, что во всякой геометрии линия восставленная на некоторой

образует углы α и β вместе равные двум прямым. Значит это соотношение перепишется в виде: ∑△ADC + ∑△DBC – 2∟ = ∑△ABC. Значит (исходя из этого соотношения) если каждый из треугольником ADC и DBC имеет сумму углов 2∟, то их общая сумма будет 4∟ и вычитая из неё 2∟ (согласно приведённому соотношению), мы получим сумму углов треугольника ABC равную двум прямым. Если же каждый из треугольников ADC и DBC имеет дефект (соответственно ε1 и ε2) то их общая сумма углов (треугольников ADC и DBC) будет меньше четырёх прямых на сумму их дефектов. Значит и вычитая из неё 2∟ (согласно формуле) мы будем иметь величину меньшую двух прямых на сумму дефектов (ε1 + ε2). Эта же величина есть ∑△ABC. Значит ∑△ABC меньше двух прямых на (ε1 + ε2). Значит дефект треугольника ABC равен сумме дефектов треугольников его составляющих. Значит дефект всякого треугольника, разделённого на два некоторых, равен сумме их дефектов – то есть дефект аддитивен.

{

Ещё доказательство этой теоремы может быть записано так:

Пусть ∑△ADC = 2∟ – ε1 и ∑△DBC = 2∟ – ε2,

Тогда ∠1 + ∠2 + ∠6 = 2∟ – ε1, а ∠3 + ∠4 +∠5 = 2∟ – ε2

значит ∠1 + ∠2 + ∠6 + ∠3 + ∠4 +∠5 = 2∟ – ε1 + 2∟ – ε2

Но ∠5 + ∠6 = 2∟ значит

∠1 + ∠2 + ∠3 + ∠4 = 2∟ – ε1 – ε2 (вычли из левой части углы 5 и 6, а из правой 2∟)

Но ∠1 + ∠2 + ∠3 + ∠4 = ∑△ABC

Значит ∑△ABC = 2∟ – ε1 – ε2

Или так: ∑△ABC = ∑△ADC + ∑△DBC – 2∟ = (2∟ – ε1 + 2∟ – ε2) – 2∟ = (4∟ – ε1 – ε2) – 2∟ = 2∟ – ε1 – ε2

}

Вернёмся теперь к нашему построению и соединим точки T1 и N2.

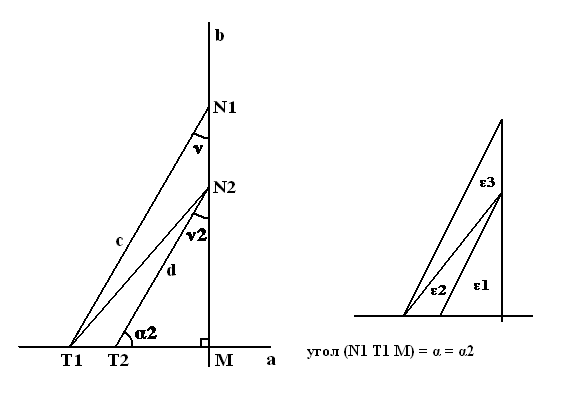
Тогда если дефект треугольника (T2 M N2) равен ε1 (Д△(T2 M N2) – дефект треугольника T2 M N2), а дефект треугольника (T1 T2 N2) равен ε2, то дефект треугольника (T1 M N2) равен ε1 + ε2. Рассмотрим теперь треугольник (T1 M N1) – он состоит из треугольников (T1 M N2) и (T1 N2 N1). И пусть теперь дефект треугольника (T1 N2 N1) равен какой–нибудь величине ε3. Тогда раз Д△(T1 M N2) = ε1 + ε2, а Д△(T1 N2 N1) = ε3, то Д△(T1 M N1) = Д△(T1 M N2) + Д△(T1 N2 N1) = ε1 + ε2 + ε3. Значит Д△(T1 M N1) = ε1 + ε2 + ε3.

Значит поскольку дефект, это величина, на которую сумма углов треугольника меньше двух прямых, то ∑△(T1 M N1) = 2∟ – ε1 – ε2 – ε3.

А поскольку угол ν = ∑△(T1 M N1) – α – ∟ то,

ν = 2∟ – (ε1 + ε2 + ε3) – α – ∟ = ∟ – α – (ε1 + ε2 + ε3)

Угол же ν2 равен ∑△(T2 M N2) – α – ∟ = 2∟ – ε1 – α – ∟ = ∟ – α – ε1

Значит ν = ∟ – α – ε1 – ε2 – ε3, а ν2 = ∟ – α – ε1 то есть ν < ν2 на величину ε2 + ε3 и возвращаясь к первоначальному построению можно сказать, что «линия» (d), продолжаясь пересечёт «линию» (b) не под тем же углом что и «линия» (c). (ν2 > ν)

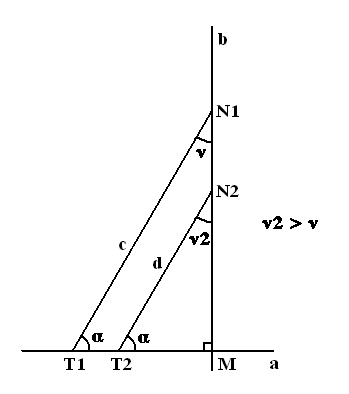
Значит из того, что в геометрии Лобачевского сумма углов треугольника отличается от двух прямых (менее двух прямых) следует и то, что в ней не все треугольники имеют одинаковую сумму углов. [18]

Рассмотрим теперь случай более общий, чем рассматриваемые в общей геометрии – пусть сумма углов треугольника будет не обязательно меньше 2∟ – и докажем следующую теорему: геометрия в которой сумма углов всех треугольников одинакова и равна 2∟ является единственной геометрией в которой сумма углов всех треугольников одинакова.

Пусть существует некоторая геометрия в которой сумма углов всех треугольников одинакова и равна H.

И пусть в ней некоторый треугольник ABC разделён на два других (ADC и DBC, как показано на рисунке)

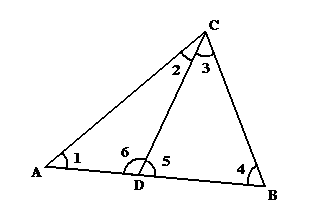
Тогда проведём ещё раз доказательство формулы ∑△(ABC) = ∑△(ADC) + ∑△(DBC) – 2∟ *

*{ ∑△ADC = ∠1 + ∠2 + ∠6, а ∑△DBC = ∠3 + ∠4 + ∠5

∑△ADC + ∑△DBC = ∠1 + ∠2 + ∠6 + ∠3 + ∠4 + ∠5

Но ∑△ABC = ∠1 + ∠2 + ∠3 + ∠4

Значит ∑△ABC = ∑△ADC + ∑△DBC – ∠5 – ∠6

а так как ∠5 + ∠6 = 2∟

то ∑△ABC = ∑△ADC + ∑△DBC – 2∟

}

Значит в любой геометрии сумма углов треугольника, разделённого на два некоторых, выражается через их суммы следующим образом:

∑△ABC = ∑△ADC + ∑△DBC – 2∟

Пусть теперь в нашей геометрии сумма углов всех треугольников одинакова и равна H,

тогда ∑△ABC = ∑△ADC = ∑△DBC = H и уравнение перепишется в виде

H = H + H – 2∟ → H = H + x → x = 0 → H – 2∟= 0 → H = 2∟

Значит мы доказали, что геометрия Евклида (геометрия в которой сумма углов всех треугольников одинакова и равна двум прямым) является не просто частным случаем более общей геометрии, открытой Н. И. Лобачевским, но и единственной геометрией в которой сумма углов всех треугольников одна и та же.

ПОЯСНЕНИЯ К ДОКАЗАТЕЛЬСТВУ

Нас интересует, может ли существовать геометрия в которой суммы углов всех треугольников одинаковы и равны (каждая) при этом некоторой величине H – не равной двум прямым. Если такая геометрия существует, то величина H либо больше двух прямых, либо меньше. Пусть H < 2∟. Примем также, что всякий треугольник может быть разделён на два других – так на любой его стороне, произвольным образом берётся точка и соединяется с противоположной вершиной.

Тогда суммы углов треугольников его составляющих одинаковы (равны H) и каждая меньше двух прямых на некоторый (один и тот же) дефект ε1. Тогда дефект целого треугольника (разделённого на эти два) равен ε1 + ε2 и значит его сумма углов отличается от двух прямых не на ту же величину, что и сумма углов каждого из составляющих его треугольников. Значит, его сумма углов отличается от суммы углов каждого из составляющих его треугольников. Значит, в данной геометрии существуют треугольники с разной суммой углов. Подобным же образом это доказывается и для случая H > 2∟. Там используется теорема аналогичная теореме об аддитивности дефектов треугольников.

Заключение

Положения Евклидовой геометрии являются фундаментальными принципами геометрии вообще, и отклонение от них в ту или другую сторону приводит нас к той или иной неевклидовой геометрии.

Во-первых хочется сказать, что я очень надеюсь, что теперь Вы уже немного разобрались в основах этой науки (конечно если раньше не разбирались) и, главное, надеюсь, – что Вы увидели красоту оснований Геометрии. Перейдём теперь к решению нашего вопроса и рассмотрим вот что. – Лобачевский называет свою геометрию Воображаемой, а Евклидову – Употребительной. Видимо подчёркивая близость Евклидовой геометрии к окружающему миру. Но только ли в этом состоит различие и отношение двух геометрий? Часто отношение между Евклидовой и "альтернативными" геометриями представляют упрощённо – лишь как отношение между вещами разными и одинаково правильными – как отношение между правой и левой перчатками, разными видами деревьев или отношения между квадратом и окружностью – с тем лишь отличием что Евклидова геометрия описывает окружающий мир. В действительности же отношение между Евклидовой геометрией и геометрией Лобачевского напоминают скорее отношение между окружностью и эллипсом в том смысле, что эллипс это в некотором смысле видоизменённая окружность– окружность с поправкой–возмущением – эксцентриситетом, при стремлении которого к нулю эллипс переходит в окружность. Так и геометрия Лобачевского это в некотором смысле основная (Евклидова) геометрия с некоторым возмущением при стремлении которого к нулю неевклидова геометрия переходит в основную. (дальше я ещё поясню это на примере). – то есть разные геометрии логически неравноправны.

Очень хорошо это отражают термины – искривлённое пространство и плоское пространство в том смысле, что Евклидово пространство является – основным (плоским) пространством по отношению к которому все другие пространства являются искривлёнными – как бы имеющими некоторое возмущение по отношению к основному, – и при этом все теоремы Евклидовой геометрии сохраняют абсолютную истинность как теоремы простейшего – основного пространства Геометрии.

Или как теоремы Геометрии в самом общем смысле этого слова – повествующие об отношениях в простейшем из всех пространств.

Таким искривлением – возмущением – можно считать отличие в этих пространствах суммы углов треугольников от двух прямых – константы – значения суммы углов, единственно обеспечивающего равенство всех таких сумм.

Но это можно понять и на другом более наглядном примере – пусть в Евклидовой геометрии – плоском пространстве – пересекаются две прямые – (а) и (b) – под углом α, как показано на рисунке.

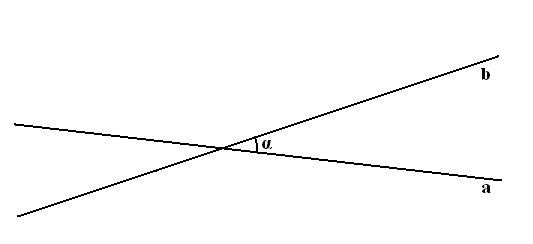
пусть теперь на прямой (b) восставлена под некоторым углом β – прямая (с) и продолжена пунктиром – как показано на рисунке – до пересечения с прямой (а) (и пусть β + α меньше двух прямых[19])

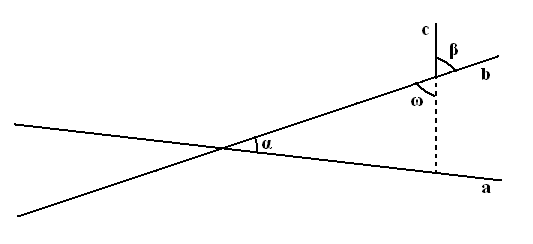
Их внешний угол при пересечении будет равняться α + ω (как внешний двум внутренним – противолежащим – тридцать втрое предложение Начал) или что то же самое α + β.

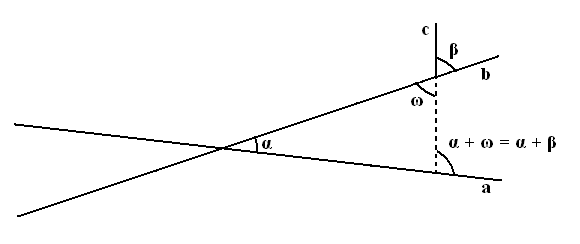
Но это видно и из следующих соображений – прямая (b) отличается от прямой (а) на угол α, а прямая (с) отличается от прямой (b) на угол β в ту же сторону. Значит прямая (с) должна отличаться от прямой (а) на угол равный углу α и β взятым вместе. – что мы и имеем.

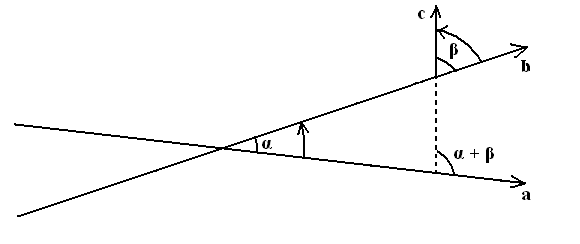
Причём угол пересечения прямой (с) с прямой (а) не будет зависеть от того в какой точке прямой (b) прямая (с) – восставлена.

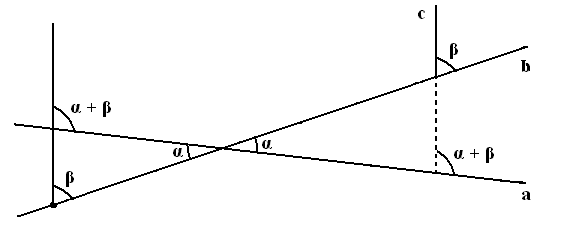
Таким образом в плоском пространстве угол между линиями определяется углом их пересечения между собой и обратно, – и не зависит от расстояний. – углы определяются только углами. – искривление же пространства надо (можно) понимать как отступление от этого закона. Так, например, если бы мы выполнили подобное построение в геометрии Лобачевского, то оказалось бы, что получившийся угол больше того который бы был в геометрии Евклида как раз на дефект треугольника (ε).

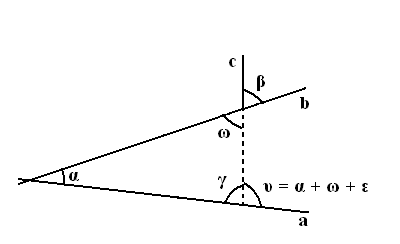
Действительно α + ω + γ + ε = 2∟ и υ + γ = 2∟, значит υ = α + ω + ε.

ПОЯСНЕНИЯ К ЗАКЛЮЧЕНИЮ

Здесь мы говорим о некотором свойстве-принципе пространства, отступление от которого нами и мыслится как его (пространства) искривлённость. Несколько по-другому его формулирует Лобачевский. Он говорит о зависимости углов треугольника (в геометрии Евклида) только от отношения между его сторонами и независимости углов от их (сторон) величины. У Лобачевского об этом так < Из всех известных подобных положений отдать надобно преимущество тому, которое принимает зависимость содержания линий[20] от углов; по крайней мере здесь простота в понятии близка даже к первой нашей опытности >[21]. Действительно, в таком случае существуют треугольники углы которых соответственно равны, но стороны одного из которых во сколько-то раз больше соответственных сторон другого - то есть подобные, но не равные треугольники. (как показано на рисунке)

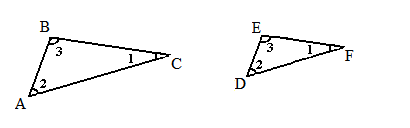
Тогда внутри большего из этих треугольников можно построить треугольник равный меньшему.

{ Отложим на BA BN = ED а на BC BM = EF. Тогда △BNM = △EDF (согласно четвёртому предложению Начал: BN = ED, ∠NBM = ∠DEF, BM = EF.) }

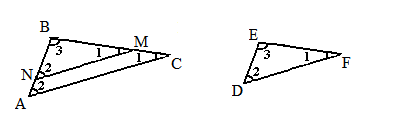
Отсюда ясно что сумма углов каждого из этих треугольников равна двум прямым ибо один треугольник заключает другой, а их суммы углов равны.

В статье Г.И.Челпанова "Неогеометрия и её значение для теории познания" это свойство (возможность существования подобных и при этом неравных треугольников) называется гомогенностью пространства. Среди прочего там приводятся такие суждения: < Гомогенность некоторыми авторами считается настолько важным свойством пространства, что если последнее им не обладает, то его не считают даже пространством в собственном смысле. Так как в не-евклидовском пространстве нет гомогенности то в этом видели доказательство невозможности метагеометрии[22], поэтому они априорным свойством пространства считали как свободную подвижность, так и возможность подобия. По этому взгляду гомогенность пространства считается априорным достоянием нашего ума, потому что она, не может быть доказана из опыта. "Можно ли сказать, спрашивает Кутюра, что этот принцип потому сделался требованием нашего духа, что мы имели возможность неоднократно констатировать увеличение и уменьшение фигур. Очевидно, что гомогенность пространства так же не может быть констатьируема опытом, как и его изогенность[23]. Поэтому идея подобия является так же априорной, как идея геометрического равенства. Если наше пространство гомогенно, то это потому, что нашему разуму противно, чтобы форма фигур зависела от их величины, или от единицы меры и чтобы пространство имело абсолютную величину[24]". (Revue de la Metaphysique et de la Morale. 1893. №3.) >

«Но должны ли мы, допуская возможность существования неевклидовых (негомогенных) пространств считать этот принцип (гомогенность) лишь произвольным положением, которому мы отдаём предпочтение только из-за того, что он хорошо согласуется со свойствами окружающего мира?

Надо полагать, что вовсе не обязательно, и более того - мы не должны так думать.

Безусловно мысль о том, что принцип гомогенности основан только на многократном наблюдении обладающих этим свойствам тел окружающего нас мира – это яркий пример очевидной нелепости, возникающей при попытке говорить об опытном происхождении математических истин. Другое дело допустима ли геометрия изучающая отклонения от этого принципа? В любом случае она будет геометрией изучающей лишь отклонения от исходных принципов разума а не что то принципиально другое.

В таком случае Евклидова геометрия отражает не непременно необходимое но нейтральное состояние пространства. То есть допуская возможность геометрии Лобачевского, мы говорим об аксиомах Евклида как об истинах уже не в том смысле что невозможны другие(отличные от них) пространственные отношения, но что аксиомы Евклида истинны как положения характеризующие некоторые исходные пространственные отношения, уже по отношению к которым в геометрии Лобачевского вводятся дополнительные зависимости (например, зависимость углов в треугольнике от размера сторон а не только от их взаимного отношения)

Значит мы приходим к тому, что никакого кризиса в основаниях Геометрии не существует, в не зависимости от того о каком подходе к пониманию нееаклидовых геометрией мы говорим. Так, если мы говорим о том подходе, который я в самом начале этой работы назвал формальным, то речь идёт просто об изучении аналогии между евклидовой геометрией и свойствами некоторых геометрических конструкций, которые мы строим в евклидовом же пространстве. При интерпретации же Гаусса-Лобачевского и предположении о существовании иных пространств мы все равно никуда не уходим от исходной – основополагающей роли[25] Евклидового пространства и его положений в отношении рассмотрения пространств – искривленных.

Эта научная работа выполнена М.А. Щукиным