 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Применение регрессионного анализа для решения обратной задачи гравиметрии
|
|
При решении геофизических задач часто используется приближение изучаемого признака y(x) линейной математической моделью:
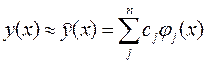 (7.1)
(7.1)
где сj- коэффициенты при j-ой, в общем случае нелинейной базисной функции φj(x).
Оценка ŷ(x) случайной величины y(x) называется регрессией y на x. Важность регрессионной модели (7.1) заключается в оптимальности прогноза величины y(x) по заданному значению аргумента [ ]. Регрессионная модель может успешно применятся для решения линейных обратных задач геофизики. В этом случае основная цель – определение коэффициентов - cj (j=1…n), которые характеризуют амплитудные множители при координатных базисных функциях – φj(x), аппроксимирующих геометрию изучаемого геологического разреза.
Для определения параметров регрессионной модели необходимо задать систему базисных функций для m точек, на которых известны значения выходной переменной y. Если m>n, то коэффициенты в уравнении (7.1) могут быть определены по методу наименьших квадратов, гарантирующему минимальную величину средней квадратической невязки между регрессией ŷ(x) и аппроксимируемой переменной y(x). Обычный способ определения коэффициентов на основе формируемой системы нормальных уравнений требует обращение матрицы размером n>n (см. лабораторную работу №). Как известно, эта процедура весьма чувствительна к ошибкам вычислений и измерений входных и выходных переменных. В работах [ ] приведены алгоритм и практические расчеты, связанные с вычислением коэффициентов cj, основанные на применении сингулярного разложения матрицы плана А. Элементами этой матрицы ai,j являются значения базисных функций: ai,j= φj(xi); i=1, …m; j=1, …n. Согласно (7.1) данные измерений на m точках можно записать в виде

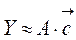 , (7.2)
, (7.2)
где 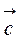 =[с1, …, сn] – вектор –столбец определяемых коэффициентов.
=[с1, …, сn] – вектор –столбец определяемых коэффициентов.
Представление матрицы А в виде сингулярного разложения [ ] позволяют преобразовать (7.2) в эквивалентную диагональную систему, решения которой следует выбирать с учетом реальной точности вычислений и исходных данных, отбрасывая элементы разложения, соответствующие сингулярным числам σj, меньшим заданной точности τ. Эта операция дает возможность более оптимального определения коэффициентов благодаря уменьшению числа обусловленности матрицы А от σ1/σn до σ1/ τ. При этом, как правило невязка между измененной y(x) и регрессионной ŷ(x) переменными возрастает, но надежность получающегося регуляризованного решения с избытком оправдывает эту потерю.
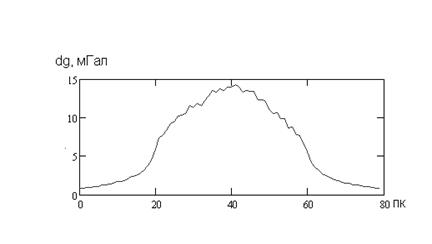
В качестве практического задания следует осуществить решение линейной обратной задачи гравиразведки с целью определения морфологии массива ортоамфиболитов, контролирующее размещение редкометальных пегматитов. Массив вытянут в горизонтальном направлении, модельный разрез которого приведен на рис. 7.1.
| v 0,35 v v v v | v 0,23 v v v v | v 0.30 v v v v | v 0,35 v v v v |
| 0,08 | v 0,44 v v v v | v 0,41 v v v v | 0,08 |
| 0,08 | v 0,36 v v v v | v 0,33 v v v v | 0,07 |
| 0,11 | v 0,28 v v v v | v 0,26 v v v v | 0,08 |
| 0,12 | v 0,22 v v v v | v 0,21 v v v v | 0,08 |
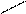
| v v | 0.35 |
Рис. 7.1 Схематический разрез массива ортоамфиболитов и гравитационное поле над ним:
1- наблюденное кривая dg; 2- ортоамфиболиты; 3- избыточные плотности- δ призм в г/см3
Для решения линейной обратной задачи аппроксимируем разрез набором из 20 горизонтальных прямоугольных призм. Их геометрические размеры в разрезе следующие: горизонтальная и вертикальная мощности, соответственно равны 1000 и 300 метров. Координата точки левого верхнего угла набора призм, относительно профиля измерения, равна x = 4000 м, глубина h =10 м. Избыточные плотности призм приведены на рисунке.
Для решения обратной задачи необходимо знать распределение гравитационного поля по профилю. Поэтому в начале, для данной геологической ситуации следует решить прямую задачу. Условимся, что длина профиля равна 8000 м, что соответствует m =80 пикетам при шаге в 100 м. Результирующее поле на каждом пикете будет равно сумме гравитационных эффектов от каждой j -ой призмы; j=1, …n; n =20.
Гравитационный эффект от одиночной прямоугольной горизонтальной призмы в точке профиля x=0 вычисляется [ ] по формуле:
dg=f∙∆δ·(x∙ln(x2+h2)+2∙h·arctg(x/h)). (7.3)
Данную формулу, для расчета поля на одном пикете от одной призмы, используют четыре раза, подставляя в неё каждый раз соответствующие координаты расчетной призмы, по логике указанной ниже:
dG = dg(x1.h1) - dg(x1.h2) - dg(x2.h1) + dg(x2.h2),
где x1, x2- координаты соответственно левой и правой граней призмы; h1, h2 – глубины до верхней и нижней кромки призмы; ∆δ- избыточная плотность призмы (в г/см3); f – гравитационная постоянная равная 66,7 ∙10-9 (см3/г·с2).
Если при расчетах все линейные (геометрические) размеры подставлять в системе СГС, т.е в сантиметрах, что может быть и не очень удобно, то результаты вычислений будут получены в Галах (1Гал = 1 см/с2 = 1000 мГал).
Полученный результат вычислений гравитационного поля обозначим через G, он будет соответствовать вектор-столбцу Y в выражении (7.2). По результатам расчета построить график поля G, его форма должна быть похожа на таковой приведенный на рис.7.1.
На следующем этапе выполнения работы следует рассчитать матрицу плана А. Как уже было сказано выше, элементами этой матрицы являются значения базисных функций ai,j, которые соответствуют эффекту j – й прямоугольной призмы (j=1, …20) в i – й точке профиля (i=1, …80), причем плотность такой призмы принята равной 1. Следовательно размер матрицы А должен быть 80 x 20.
Имея значения гравитационного поля G и матрицу плана А, можно осуществить решение обратной линейной задачи гравиметрии методом наименьших квадратов. Аналогичная процедура рассматривалась в лабораторной работе № 2, по этому здесь мы её подробно не описываем. Решение в этом случае в матричной форме записывается следующим образом:
δ0 = (АТ · А)-1 ∙ АТ ∙ G, (7.4)
где δ0 – вектор искомых значений избыточной плотности призм.
Результаты вычислений δ0 по формуле (7.4) сравнить с исходными значениями δ, используя логику формулы (2.4). Расхождение в этом случае должно быть минимальным.
Далее, чтобы показать, что обратная задача геофизики весьма неустойчивой к ошибкам измерений и вычислений, следует внести в исходное поле G помеху равную ±(3-5)%, обозначить результат через G1 и вновь вычислить по (7.4) избыточную плотность, обозначив её через δ2. Вновь провести сравнение δ2 с δ, по формуле (2.4). Расхождение между этими величинами в данном случае должны быть очень большими и неприемлемыми для решения. Дайте этому факту объяснение.
Для получения наиболее оптимального варианта решения обратной задачи, воспользуемся процедурой сингулярного разложения матрицы плана А. Но вначале в матрицу плана А добавим 21-й столбец путем присоединения к ней вектор-столбца R, все члены которого равны 1. Размерность R – (80 x 1). Данное действие позволит нам в дальнейшем получить информацию о значении фонового гравитационного поля по данному профилю.
Алгоритм этой процедуры в MachCadе следующий:
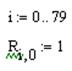
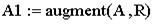
Размер матрицы А1 после этого действия должен стать (m=80 x n=21).
Сингулярным разложением действительной m x n матрицы А называется всякая её факторизация вида
А= U∙S·VT,
где U – ортогональная (m x n) матрица; VT – транспонированная ортогональная (n x n) матрица; S- диагональная матрица (n x n), у которой σi,j=0 при i≠j и σj,j = σj ≥ 0. Величины σj называются сингулярными числами матрицы А1.
Для реализации сингулярного разложения в MachCadе есть встроенная функция – svd2(A1), где A1 – входнаяматрица, для которой рассчитываются три выходных матрицы S, U, и VT. Порядок обращения к функции svd2 следующий:
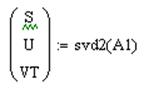 ,
,
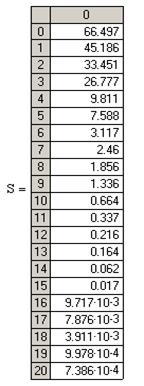
С целью проверки результатов сингулярного разложения матрицы А1, можно вычислить матрицу А0 как произведение А0= U∙diag(S)∙VT, матрицы А0 и А1 должны быть равными. Процедура diag(S) – осуществляет преобразование вектор-столбца S в диагональную матрицу. Значения вектор-столбца S в нашем случае следущие:
S = (66,50; 45,19; 33,45; 26,78; 9,81; 7,58; 3,12; 2,46; 1,86; 1,34; 0,66; 0,34; 0,22; 0,16; 0,06; 0,02; 0,01; 0,008; 0,004; 0,001; 0,0007).
Тогда число обусловленности матрицы А1 равно β= σ1 / σ21 66,5 / 0,0007= 9,5·104, это достаточно большая величина, что говорит о значительной вырожденности матрицы А1 и плохих результатах решения систем линейных уравнений обычными методами.
Если задать оптимальную точность решения 3%, то наименьшее значение сингулярного числа будет равно τ=0,03· σ1=66,5∙0,03=1,995, т.е. это соответствует использованию первых восьми сингулярных чисел k=8.
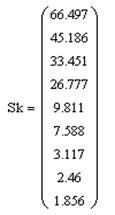
На следующем этапе следует сформировать три новых матрицы Sk, UkT и Vk, которые будут включать в себя определенные фрагменты соответствующих матриц S, U и VT. Для подобных процедур существует встроенная функция В=submatrix(D,ir,jr,ic,jc)- где, В – результирующая матрица, состоящая из строк от ir до jr, и столбцов от ic до jc исходной D матрицы.
Логика формирования новых матриц Sk, UkT и Vk приведена ниже:
Sk=submatrix(S, 0, k, 0, 0);
UkT=submatrix(U, 0, rows(U) -1, 0, k);
Vk=submatrix(VT T, 0, rows(VT) T -1, 0, k).
Размерности данных матриц для нашего случая следующие: Sk – (k x 0); UkT – (k x m); Vk – (n x k).
Далее рассчитываем псевдообратную матрицу АР, как произведение соответствующих матриц, её размерность будет (n x 1):
AP= Vk·diag(1/Sk)·UkT
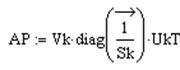
Дата публикования: 2015-10-09; Прочитано: 409 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
