Применение факторного анализа для расчета регионального фона и локальной аномалии

Как факторный, так и компонентный анализы базируются на изучении внутренней структуры ковариационной матрицы исходных данных [ ]. Это изучения включает: 1)нахождение собственных значений и собственных векторов матрицы; 2) вычисление линейных комбинаций исходных величин с собственными векторами; 3) оценку числа основных, независимых векторов; 4) физическое или геологическое истолкование факторов и главных компонент.

Рассмотрим применение факторного анализа на примере площадной гравиметрической съемки с целью выделения регионального поля и расчета локальной составляющей.

Пусть дан двухмерный массив G (рис.6.1) измеренных значений поля по N профилям, на каждом из которых M пикетов, N=8, а M=21.

Рис. 6.1 Массив измеренных значений поля G.

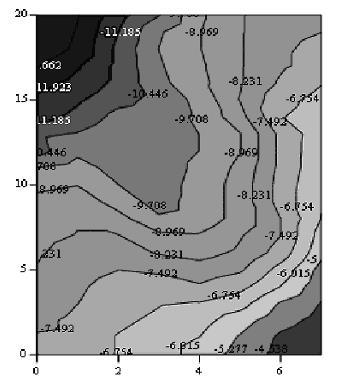
Рис. 6.2 Исходное поле G (план изомиллигал).

Анализируя характер гравитационного поля G (рис. 6.2), можно сказать, что локальную аномалия в явном виде не просматривается, и выделить её, без специальных средств обработки не представляется возможным.

Попробуем применить в этом случае факторный анализ. Для этого в начале необходимо вычислить ковариационную матрицу для массива G_b,i. Значения ковариации рассчитываются для различных пар профилей, т.е.

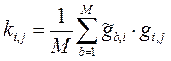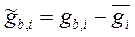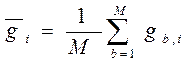; ; (6.1)

где i, j = 1….N, N-число профилей; b = 1…M, M-число пикетов по профилю; g_b,i – измеренное значение поля на b-ом на пикете, i–го профиля.

Расчет значения ковариации можно осуществлять как по самостоятельно прописанной и реализованной процедуре, на основе формулы (6.1), или с помощью встроенной функции в MachCad – cvar (X,Y), где X, Y – вектора для которых рассчитывается ковариация. По полученным ковариациям составляется ковариационная матрица, размерность которой N x N

к_1,1 к_1,2 .... к_1.N

К= к_2,1 к_2,2.... к_2.N

_{∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙}

к_N,1 к_N,2.... к_N.N,

для которой находятся максимальное собственное значение λ_max из уравнения | К-λ_max·I | = 0 и соответствующий этому значению собственный вектор- a₁ матрицы К из системы линейных уравнений (К - λ_max)·a₁=0, т.е.

(k_1,1 - λ_max) ·a_1,1+ k_1,2·a_1,2+.... + k_1,N·a_1,N =0

k_2,1·a_1,1 + (k_2,2 - λ_max) ·a_1,2+.... + k_2,N·a_1,N =0

..........................

k_N,1·a_1,1 + k_N,2·a_1,2 +.... + (k_N,N - λ_max) ·a_1,N=0

Расчеты связанные с нахождением собственных значений λ_i и собственных векторов a_i,j можно осуществлять с помощью встроенных функции MachCadа. Функция eigenvals (K) позволяет рассчитать собственные значения λ_i, для ковариационной матрицы K. Функция eigenvec (K, λ_i) предоставляет возможность расчета нормированного собственного вектора – a_i, для ковариационной матрицы К, и соответствующего i-го собственного значения- λ_i. Нормирование собственных векторов необходимо для того, чтобы преобразованные данные не отличались по масштабу от исходных. С учетом нормировки вектора ,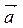

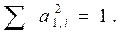
Результаты расчета собственных значений λ для нашего случая, должны быть следующими: λ = (8,206; 0,787; 0,057; 3,351 ·10^-3; 2,648 ·10^-3; 1,111 ·10^-3; 0; 1,211 ·10^-3). Анализируя величину собственных значений, видим, что самое первое значение λ₁=8,206 является самым большим (на порядок больше следующего), этот факт говорит о том, что существует некоторый геологический фактор, вносящий значительный вклад в общую дисперсию суммарного гравитационного поля. Обычно этот фактор отождествляют с региональной (фоновой) составляющей геофизического сигнала [ ]. Поэтому, с целью выделения региональной составляющей геофизического поля, следует рассчитать собственный вектор – а₁, именно для первого собственного значения λ₁. Собственный вектор –а₁, в данном задании, должен иметь размерность – N, и равен следующим значениям: а₁ = (0,414; 0,403; 0,382; 0,376; 0,335; 0,322; 0,284; 0,286). Физический смысл собственного вектора а₁ состоит в том, что он определяет весовые коэффициенты для значений поля по каждому профилю.

На следующем этапе необходимо вычислить значение первой главной компоненты Y₁= а₁G, или

g_1,1 g_1,2 · · · · · g_1,M

Y_1,b=(a_1,1; a_1,2; · · · ·; a_1,N) · g_2,1 g_2,2 · · · · · ·g_2,M

· · · · · · · · · · ·

g_N,1 g_N,2 · · · · · g_N,M ,

где, N-число профилей; M-число пикетов по профилю; g_i.b – измеренное значение поля на b-ом на пикете, i–го профиля.

При работе с матрицами полезно вспомнить правила. Например, при умножении матрицы на матрицу количество столбцов первой матрицы должно быть равно числу строк – второй. Тогда результирующая матрица будет иметь размерность - число строк первой и количество столбцов второй матриц. В нашем случае размерности матриц следующие, у вектор-строки а₁(1xN) и матрицы G(NxM). Значить, в результате их перемножения получим вектор-строку Y₁ с размерностью –(1xM).

Физический смысл первой главной компоненты Y состоит в том, что он определяет весовые коэффициенты для значений поля по каждому профилю. При этом оценка составляющей наблюденного поля, характеризующаяся наибольшей дисперсией (такой составляющей обычно является фоновая), равна произведению вектор-столбца Y₁^Т(Mx1) на вектор-строку а₁(1xN), т.е.

Y_1,1 Y_1,1·а_1,1 Y_1,1·а_1,2 · · · Y_1,1·а_1,N

GФ_b,i= Y_2,1 · (а_1,1, а_1,2, · · · · а_1,N) = Y_2,1·а_1,1 Y_2,1·а_1,2 · · · Y_2,1·а_1,N

.. · · · · · · · · · · · · · · · · · · · · · · ·

Y_M,1 Y_M,1·а_1,1 Y_M,1·а_1,2 · · Y_M,1·а_1,N

Так как GФ_b,i чаще всего является оценкой региональной составляющей, разность GЛ_b,i = G_b,i - GФ_b,i оценивает поле локальных аномалий.

После расчета фона- GФ_b,I, вычислить локальную составляющую -GЛ_b,i, дать их графическое представление в виде планов изомиллигал (рис.6.3).

Рис.6.3 Результаты оценки региональной (а) и локальной (б) составляющих гравитационного поля путем выделения первой главной компоненты.