 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Краткие сведения из теории. Где s – комплексная переменная, B(s) – полином степени m; A(s) – полином степени n.
|
|
Известно, что если модель линейной системы автоматического управления (САУ) задается в виде структурной схемы, состоящей из типовых звеньев, то связь между входом и выходом системы определяется передаточной функцией W (s), которую можно представить в виде:
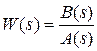 , (1)
, (1)
где s – комплексная переменная, B (s) – полином степени m; A (s) – полином степени n.
Для физически реализуемых САУ m £ n. Коэффициенты указанных полиномов действительные числа. Полюсами передаточной функции называются корни полинома – знаменателя A (s), а нулями – корни полинома числителя B (s). Применение метода корневого годографа базируется на зависимости свойств линейной САУ от полюсов и нулей ее передаточной функции. Полином A (s) называется также характеристическим многочленом передаточной функции W (s). Положение полюсов W (s) на комплексной плоскости определяет устойчивость САУ, а в совокупности с нулями – вид импульсной переходной w (t) и переходной h (t) функций.
Метод корневого годографа позволяет находить полюса и нули передаточной функции замкнутой системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы K. Передаточную функцию разомкнутой системы Wp (s) представим в виде:
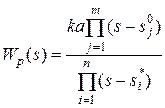 , (2)
, (2)
где 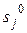 - нули передаточной функции Wp (s), (
- нули передаточной функции Wp (s), (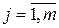 );
);  – полюса передаточной функции Wp (s), (
– полюса передаточной функции Wp (s), (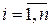 ), n и m – порядки знаменателя и числителя; k - коэффициент усиления разомкнутой системы; a – коэффициент, получающийся при разложении числителя и знаменателя передаточной функции Wp (s) разомкнутой системы.
), n и m – порядки знаменателя и числителя; k - коэффициент усиления разомкнутой системы; a – коэффициент, получающийся при разложении числителя и знаменателя передаточной функции Wp (s) разомкнутой системы.
Передаточная функция разомкнутой системы, как правило, задается в виде отношения произведений передаточных функций стандартных (типовых) звеньев, при описании которых используются выражения трех видов:
Ts; (3)
Ts +1; (4)
T 2 s 2 + 2 Txs + 1. (5)
Здесь Т – постоянная времени, x - коэффициент затухания.
Если выражения (3–5) стоят в знаменателе передаточных функций звеньев, то они называются соответственно интегрирующим, апериодическим, колебательным (0< x <1). Если выражения (3–5) стоят в числителе передаточной функции (1), то звенья называются соответственно дифференцирующим, форсирующим первого порядка и форсирующим второго порядка. Для перехода от стандартной формы записи к формуле (2) необходимо вычислить полюса и нули соответствующих типовых звеньев.
Нули и полюса для передаточных функций, использующих выражения (3–5), находятся из формул:
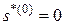 , (6)
, (6)
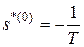 , (7)
, (7)
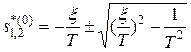 (8)
(8)
или
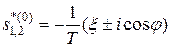 , (9)
, (9)
где j = arcsin x.
Коэффициент а вычисляется по формуле
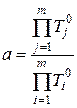 . (10)
. (10)
Для звеньев, использующих выражение (5), соответствующая постоянная времени входит в выражение (10) в квадрате.
При замыкании системы с передаточной функцией W p(s) единичной обратной связью передаточная функция замкнутой системы Wз (s) принимает вид:
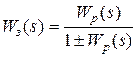 , (11)
, (11)
где знак "+" соответствует отрицательной обратной связи; знак "–" – положительной обратной связи.
Из (11) следует, что нули передаточной функции замкнутой системы равны нулям передаточной функции разомкнутой системы. Для определения полюсов замкнутой системы необходимо решить уравнение
Wp (s) = – 1. (12)
Так как Wp (s) является функцией комплексного переменного s, то уравнение (12) распадается на два уравнения:
– уравнение модулей:
| Wр (s)|=1, (13)
 – уравнение аргументов:
– уравнение аргументов:
arg Wр (s) = ± (2 n +1) p, n =0, 1, 2, …
(14)
arg Wр (s) = ± 2p, n =0, 1, 2, …
соответственно для отрицательной и положительной обратных связей.

| Уравнения (14) имеют наглядный геометрический смысл (рис. 1). Если точка s является полюсом замкнутой системы, то проведя в точку s вектора из всех нулей Wp (s) (аргументы этих векторов обозначены 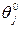 ) и вектора из всех полюсов Wp (s) (аргументы обозначены ) и вектора из всех полюсов Wp (s) (аргументы обозначены 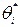 ), первое уравнение (14) можно записать в следующем виде: ), первое уравнение (14) можно записать в следующем виде:
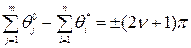 , n = 0,1,2,…, (15)
а второе в виде: , n = 0,1,2,…, (15)
а второе в виде:
|
| Рис. 1. Геометрическая интерпретация корневых годографов на плоскости корней |
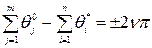 , n = 0, 1, 2, … (16)
, n = 0, 1, 2, … (16)
Углы q отсчитываются от положительного направления действительной оси. Знак угла "+" соответствует повороту против часовой стрелки, знак угла "–" соответствует повороту по часовой стрелке.
Траектории, описываемые на комплексной плоскости корнями характеристического уравнения замкнутой системы при плавном изменении одного из ее параметров от 0 до ¥, называют корневым годографом.
Как следует из (15) и (16), конфигурация корневого годографа не зависит от коэффициента усиления k, но каждому конкретному значению k однозначно соответствуют точки на корневом годографе.
Для определения этого соответствия достаточно воспользоваться уравнением (13) в следующей интерпретации:
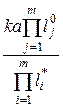 , (17)
, (17)
где 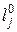 – модуль (длина) вектора, проведенного из j -нуля в точку s корневого годографа;
– модуль (длина) вектора, проведенного из j -нуля в точку s корневого годографа; 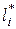 – модуль вектора, проведенного из i -полюса в ту же точку s.
– модуль вектора, проведенного из i -полюса в ту же точку s.
Свойства корневых годографов (случай отрицательной обратной связи)
1. Ветви корневого годографа непрерывны и расположены на комплексной плоскости симметрично относительно действительной оси.
2. Число ветвей корневого годографа равно порядку системы n. Ветви начинаются в n полюсах разомкнутой системы при k = 0. При возрастании k от 0 до ¥ полюса замкнутой системы двигаются по ветвям корневого годографа.
3. Отрезки действительной оси, по которым перемещаются действительные полюса замкнутой системы, являются действительными ветвями корневого годографа. Эти ветви находятся в тех частях действительной оси, справа от которых расположено нечетное общее число действительных полюсов и нулей разомкнутой системы.
4. m ветвей корневого годографа при возрастании k от 0 до ¥ заканчиваются в m нулях Wp (s), a (n – m) ветвей при k, стремящемся к ¥, удаляются от полюсов вдоль асимптот.
5. Асимптоты в виде звезды из (n – m) полупрямых выходят из точки с координатой
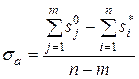
на действительной оси под углами
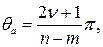
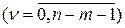
к действительной оси.
6. Угол выхода 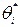 ветви корневого годографа из полюса s i* определяется из уравнения (15), примененного к данному полюсу. Аналогично определяется угол входа ветви корневого годографа в нуль s j0.
ветви корневого годографа из полюса s i* определяется из уравнения (15), примененного к данному полюсу. Аналогично определяется угол входа ветви корневого годографа в нуль s j0.
7. При расположении ветвей корневого годографа в левой полуплоскости s САУ устойчива. При пересечении ветвей корневого годографа мнимой оси слева направо САУ становится неустойчивой. Пусть при k = k кр пересечение корневого годографа с мнимой осью произойдет в некоторой точке iw кр. Назовем это значение коэффициента усиления критическим k кр, а величину w кр критической угловой частотой, на которой система становится неустойчивой.
Метод корневого годографа позволяет выбрать коэффициент усиления САУ, подобрать расположение полюсов и нулей передаточной функции корректирующих звеньев, определить параметры доминирующих полюсов САУ (ближайших к началу координат плоскости s).
Дата публикования: 2015-09-18; Прочитано: 207 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
