Лекция 6. Метод точечных преобразований

План лекции

1. Принцип точечного преобразования

2. Применение метода точечных преобразований для систем второго порядка

3. Определение устойчивости и характера переходных процессов с помощью метода точечных преобразований

Содержание лекции

Метод точечных преобразований позволяет определить существование автоколебаний в нелинейной системе, устойчивость или неустойчивость предельного цикла без построения фазовых траекторий. Известно, что нелинейные системы в большинстве случаев описываются сложными дифференциальными уравнениями. Поэтому целесообразно провести не всё построение фазовой траектории, а рассмотреть изменение фазовой траектории того участка, описание которого можно сделать по приближенному линейному дифференциальному уравнению без особых затруднений. Затем по этому отдельному участку можно судить о возможности или невозможности возникновения автоколебаний. В принципе, этот метод пригоден для системы любого порядка, но если порядок дифференциального уравнения выше третьего, то возникают трудности в расчёте.

Рассмотрим применение этого метода для системы второго порядка с трёхпозиционным реле с гистерезисом (рис. 2.15). Фазовая траектория это системы показана на рис. 2.16.

Чтобы исследовать динамику системы по этому методу, необходимо выяснить, как в зависимости от начальных условий перемещается точка М0 по оси абсцисс. Для этого вся фазовая траектория (см. рис. 2.16) разделяется на отдельные участки:

I участок. От значения x > a2, когда реле включено (+b) до отключения реле при xвх = a1 (см. рис. 2.16)

Рис.2.15. Трехпозиционное реле с гистерезисом

Рис.2.16. Фазовая траектория системы с трехпозиционным реле

II и VI участок. Реле отключено; движение системы за счёт инерционности системы.

III участок. Реле включается с противоположным знаком своей выходной величины (-b) при x < - a2..

I участок. Реле снова включилось (+b) при xвх > a2.

Из всех участков рассмотрим изменение фазовой траектории на оси +x. Допустим, что начальное положение изображающей точки системы М 0, где х(0) = х 0. Изображающая точка будет двигаться по соответствующим траекториям и снова приходит на ось + х в точку М 0*,где х * < х 0. Если при любых значениях х0 оказывается, что х * всегда меньше х 0, то система имеет затухающий и поэтому устойчивый переходный процесс. Но если х * > х 0, то это свидетельствует о расходящемся и поэтому неустойчивом процессе. Возможен и третий случай, когда при заданном х0 получаем равенство х * = х0. Система снова вернулась в исходное состояние. Это значит, что система имеет предельный цикл (автоколебания). Сразу возникает вопрос: эти автоколебания устойчивые или неустойчивые? По методу точечных преобразований это решается достаточно просто.

Пусть свободное движение системы при включённом реле на участке I

описывается уравнением

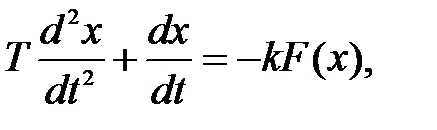
где F(x) – характеристика реле.

Уравнение фазовой траектории x=T kF(x) ln(y – kF(x)) – Ty + C₀,

где С₀ – начальные условия.

Пусть начальные условия C₀ соответствуют значениям x₀ и y₀. Уравнение фазовой траектории на участке 1 с учетом этих начальных условий при F(x)=b

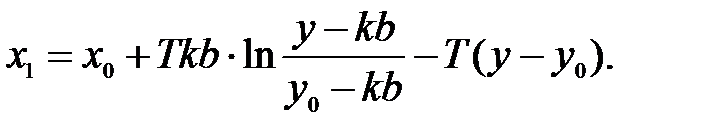
Рассмотрим на участке 1 изменение положения точки M₀ (при x(0)=x₀, y(0)=0) до M₀^’ (при x₁, y=0). Это характеризует изменение координаты по оси x на величину Δx (при F(x)=b и y=0).

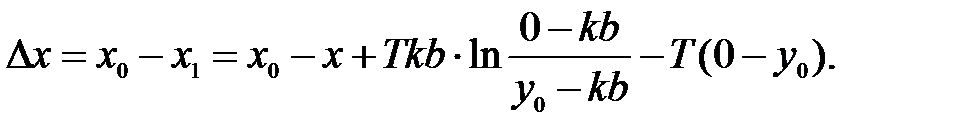
Изменение положения точки М0. не зависит от y. Величина y для обоих значений М0 и М0 равна 0. Это изменение Δx зависит от начального значения х0. В результате получаем зависимость x1 = f(x0).

Для анализа системы строим график, где ось абсцисс – состояние системы выраженное через начальное значение точки х0. Ось ординат – вычисленное значение точки х1 (рис. 2.17).

На этом графике проводим биссектрису координатного угла, т.е. прямую под углом 45⁰. Эта биссектриса характеризует те точки фазовой траектории где х0i = х1 или те значения х0i, когда фазовая траектория возвращается в первоначальное состояние (предельный цикл). Возможны следующие случаи взаиморасположения кривой х1 = f(х0) и прямой х1= х0.

1. Кривая х1 = f(х0) расположена справа от прямой х0 = х1 и её не пересекает (рис. 2.17). При любом начальном значении х0 процесс сходящийся к конечному значению х0*. Система устойчива “в общем”.

Рис.2.17. Характеристика x₁=f(x₀) справа от x₁=x₀

2. Кривая х₁ = f(х0) расположена справа от х0 = х1 и её касается в точке N1 (рис. 2.18). При х0 > C1 процесс сходится к полуустойчивому предельному циклу в точке N1 и легко может сойти с него. При х0 < C1 процесс сходится к значению х0*. Система устойчива “в общем”, но возможен режим автоколебаний при х0 = С1.

3. Кривая х1 = f(х0) и прямая х0 = х1 имеют две точки пересечения N1 и N2. (рис. 2.19). Возможны три варианта поведения системы:

– при х01 < С1 система движется к значению х0*. Система устойчива

“в малом”;

– при С1 < х02 < С2 система движется к N2. Значение х1 = f(х0) увеличивается. Система неустойчива “в малом”, величина х02 возрастает до С2, где х0** = С2 – устойчивый предельный цикл. Система устойчива “в большом”;

– при х03 > С2 система возвращается к значению N2, величина х03 уменьшается до х**0 = С2. Система тоже устойчива “в большом”. Система имеет два предельных цикла. При х0 = С1 неустойчивый предельный цикл (точка N1). При х0 = С2 устойчивый предельный цикл (точка N2).

Рис.2.18. Характеристика x₁=f(x₀) касается x₁=x₀

Рис.2.19. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в двух точках

4. Кривая х1 = f(х0) имеет одну точку пересечения N1 (рис. 2.20). Устойчивость системы зависит от значения х0 относительно C1:

– при х01 < C1 система движется к *0 x. Система устойчива “в малом”

– при х02 > C1 значение х0 возрастает. Система неустойчива “в большом”. Система имеет один неустойчивый предельный цикл в точке N1.

Рис.2.20.. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в одной точке

5. Кривая х1 = f(х0) имеет одну точку пересечения N 2 (рисунок 2.21). При любом значении х0 система стремится к точке N2. Если х01 < C1, то значение х0 увеличивается до х0 = C2. Система неустойчива “в малом”. Если х02 > C1, то значение х0 уменьшается до х0 = C1. Система устойчива “в большом”. Она имеет один устойчивый предельный цикл в точке N2 при х0= C1.

Рис.2.21.. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в одной точке

6. Кривая х1 = f(х0) расположена слева от прямой х1 = х0 и нигде не пересекается (рисунок 2.22). Если нет точки пересечения, то нет предельного цикла. При любом значении х0 значение x1 = f(х0) увеличивается. Система неустойчива “в малом” и “в большом”, она неустойчива “в общем”.

Такой расчёт можно сделать по изменению скорости движения системы y1 = f (y0) относительно y1 = y0, Это зависит от того, на каком участке движение системы проще получить и анализировать уравнение фазовой траектории.

Рис.2.22. Характеристика x₁ = f(x₀) слева от x₁ = x₀

Контрольные вопросы для самоподготовки

1. Что можно определить методом точечных преобразований?

2. В чем преимущество анализа системы методрм точечных преобразований?

3. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система устойчива «в общем»?

4. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система неустойчива?

5. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система устойчива «в малом» и неустойчива «в большом»?

6. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система неустойчива «в малом» и устойчива «в большом»

7. Что характеризует прямая x₁ = f(x₀)?

8. Как выбирается участок фазовой траектории для анализа систем методом точечных преобразований?

Лекция 7. Метод гармонической линеаризации (начало)

План лекции

1. Основные положения

2. Определение гармонической передаточной функции релейного элемента с зоной нечувствительности

Содержание лекции

Под этим общим названием объединяются группы методов анализа нелинейных систем, основанных на анализе амплитудно-частотных характеристик, возникающих в нелинейных системах. Он основан на принципе гармонического баланса разработанным Н.М.Крыловым и Н.Н.Боголюбовым. Применительно к автоматическим системам принцип гармонического баланса разработан Е.П.Поповым. Этот метод определяет возможность возникновения в системе автоколебаний, условия возникновения устойчивого колебательного режима и параметры этого автоколебательного режима.

В дальнейшем будет рассмотрен анализ не всех видов нелинейных систем, а значительно узкий класс, в котором нелинейный элемент является безинерционным звеном со статической характеристикой. Зависимость между входной и выходной величиной в таких нелинейных элементах описывается нелинейными алгебраическими неравенствами. Если система содержит несколько таких нелинейных элементов (НЭ), то данный метод расчета пригоден в том случае, если возможно заменить эти НЭ одним с результирующей статической характеристикой. Для исследования таких нелинейных систем используется линейная теория частотных методов анализа автоматических систем. Она основана на гипотезе низкочастотного фильтра линейной части системы и на предположении о гармоническом характере свободного движения в нелинейной системе.

По этому методу исследования выбирается некоторая расчетная структурная схема, в которой нелинейный элемент (НЭ) выделен в качестве входного звена, а вся остальная линейная часть (ЛЧ) системы объединена в одну общую передаточную функцию, которая располагается после нелинейного элемента (рис. 2.23). Рассмотрим прохождение некоторого гармонического сигнала через нелинейный элемент в виде идеального реле. Если сигнал на входе НЭ является синусоидальным x(t) = Asin ω t, то на выходе НЭ получаем гармонический сигнал y(t) = F(x) = F(Asin ω t)

Функция F(Asin ω t) является периодической и может быть разложена в

ряд Фурье.

Y(t) = x + Σ (Bk sin ω k t+Сk cos ω k t)

Прохождение синусоидального сигнала через нелинейный элемент показано в расчетно-структурной схеме (рис. 2.21).

Рис.2.23. Расчетная структурная схема нелинейной системы

Следовательно, на линейную часть системы (ЛЧ) действует сигнал, содержащий весь спектр частот (после разложения их в ряд Фурье), которые возникли в нелинейном элементе (НЭ). В силу принципа суперпозиции в линейной части системы каждая гармоника действует независимо от остальных. Амплитуда каждой гармоники на выходе линейной части системы z(t) будет зависеть от динамических свойств этой линейной части. Изменение амплитуды высокочастотных гармоник показано на рисунке 2.24.

Величину такого изменения можно определить по амплитудной характеристике линейной части системы.

Пусть при заданном значении частоты входного сигнала ω1 амплитуда равна) (1ω A). Если при других частотах ω2 = 2 ω 1, ω3 = 3 ω 1, ω4 =4 ω 1, и т.д. амплитуды значительно меньше, то линейную часть (ЛУ) системы можно считать фильтром низких частот, который не пропускает высшие гармоники, порождённые нелинейным элементом и на выходе ЛЧ остается только первая гармоника.

Рис.2.24. Амплитудная характеристика линейной части системы

Таким образом, расчет колебаний в нелинейной системе производится при выполнении двух условий:

- на вход нелинейного элемента (НЭ) поступает гармонический сигнал с заданной частотой;

- линейная часть системы (ЛЧ) обладает свойством низкочастотного фильтра и гасит все высшие гармоники, порождаемые нелинейным элементом.

На выходе системе рассматривается только первая гармоника. На рис. 2.23 эта первая гармоника на графике z(t) показана жирной линией.

Прежде чем выполнять анализ нелинейной системы методом гармонической линеаризации необходимо преобразовать структурную схему системы так, чтобы в ней выделялась линейная часть системы и нелинейный элемент с соответствующей статической передаточной характеристикой. Так как в заданной структурной схеме есть нелинейное звено, то это существенно ограничивает возможности структурных преобразований по сравнению с структурными преобразованиями в линейных системах. Главная причина в том, что в нелинейных системах не выполняется принцип суперпозиции (когда реакция системы на сумму воздействий равна сумме реакции на каждое воздействие). Кроме этого, в нелинейных системах не выполняется принцип коммутативности (перестановочности, когда ab = ba).

В связи с этим не все правила преобразования структурной схемы, которые используются для линейной системы, подходят для нелинейной системы.

Правила получения эквивалентной передаточной функции при последовательном, параллельном и встречно-параллельном соединении нелинейных звеньев такие же, как в линейных системах. Перемещение нелинейного звена через узел разветвления по направлению или против направления сигнала – то же аналогичные. Недопустимы следующие преобразования структурной схемы с нелинейными элементами:

- перемещение нелинейного звена через другое звено (кроме звена с запаздыванием), так как в нелинейной системе не выполняется принцип коммутативности;

- перемещение нелинейного звена через суммирующий узел, так как в нелинейной системе не выполняется принцип суперпозиции.

Определим для начала гармоническую передаточную функцию нелинейного элемента с однозначной характеристикой. Пусть на вход нелинейного звена в виде релейного элемента с зоной нечувствительности (рис.2.25, а) подан синусоидальный сигнал (рис. 2.25, б). На выходе релейного элемента возникает последовательность прямоугольных импульсов (рис. 2.25, в).

Рис.2.25. К определению гармонической передаточной функции

Высота импульсов соответствует выходной величине реле. Частота следования импульсов полностью совпадает с частотой входного синусоидального сигнала. Ширина импульса зависит от амплитуды входного сигнала A. С увеличением A ширина импульсов увеличивается.

Полученную функцию выходного сигнала разложим в ряд Фурье с учетом, что входной сигнал центрированный (x0 = 0) и расчет ведется по первой (основной) гармонике.

y(t) = B1 sin ω t + C1 cos ω t

Учитывая, что петли гистерезиса нет, то C1 = 0.

На вход релейного сигнала подана вся синусоида от ωt= 0 до ωt=2 π, поэтому величина двух полученных импульсов определяется уравнением

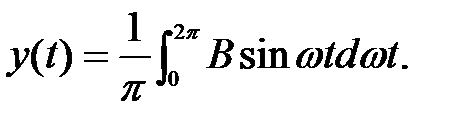
По рисунку 2.25, б видно, что реле срабатывает при входном сигнале

больше зоны нечувствительности или A sin ω t1 ≥ a1. На участке от 0 до ω t1 выходного сигнала нет. Следовательно, интегрирование надо осуществлять с момента ω t1. Поскольку выходной сигнал с реле симметричен, то можно изменить пределы интегрирования (так проще взять интеграл).

Интегрирование будет выполняться в пределах от ωt1 до π /2. Эта часть входного и выходного сигнала на рисунках 2.25 б, в заштрихована. Затем полученный результат надо учетверить, чтобы получить значение импульсов от всей синусоиды от ω t = 0 до ω t = 2 π. В результате определяем y(t)

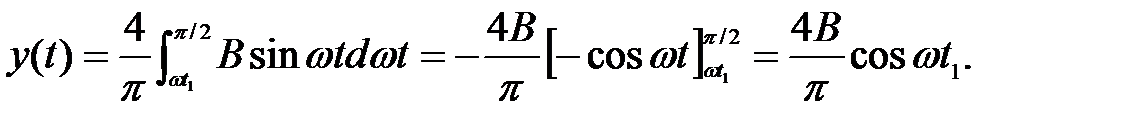
В полученном уравнении выразим cos(ωt₁) через sin(ωt₁)

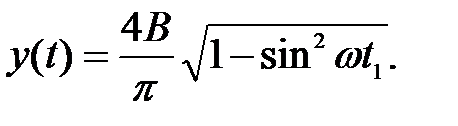
Значение sin ω t1 связано с амплитудой входного сигнала А и зоной нечувствительности реле а следующим соотношением

Asinωt = a или sinωt=a/A.

Подставим это значение sin ω t1 в выражение y(t) и получаем значение амплитуды выходного сигнала в зависимости от амплитуды входного сигнала и зоны нечувствительности реле

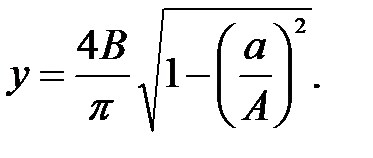
Чтобы получить передаточную функцию релейного элемента с зоной нечувствительности надо взять отношение первой гармоники выходного сигнала к входному сигналу. В данном случае входной сигнал – это амплитуда входного сигнала А. При изменении входного сигнала А изменяется значение передаточной функции. Поэтому она обозначается W(A).

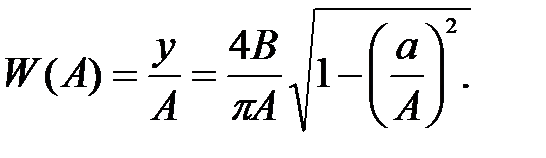
Эту передаточную функцию еще называют: гармонический коэффициент преобразования нелинейного элемента, передаточная функция эквивалентного линейного звена, гармоническая передаточная функция (Г-ПФ). Гармоническая, так как она характеризует по амплитуду первой гармонике ряда Фурье выходного сигнала.

Метод гармонической линеаризации релейного элемента называют амплитудной интерполяцией, так как полученная Г-ПФ характеризует зависимость амплитуды выходного сигнала от амплитуды входного сигнала и не зависит от изменения частоты входного сигнала. Такая амплитудная интерполяция для большинства инженерных расчетов дает достаточно адекватный результат расчета.

Лекция 8.Метод гармонической линеаризации (продолжение)

План лекции

1. Определение гармонической передаточной функции идеального реле

2. Определение гармонической передаточной функции релейного элемента с гистерезисной характеристикой

3. Определение амплитуды и частоты автоколебаний

Содержание лекции

Рассмотрим получение гармонической передаточной функции (Г-ПФ) идеального реле. Выходной сигнал будет иметь вид, показанный на рис. 2.26.

После аппроксимации выходного сигнала первым членом ряда Фурье в виде амплитуды выходного сигнала (на рис.2.26 показано штриховой жирной линией), получаем пределы измерения четверти выходной синусоиды от ωt = 0 до ωt = π /2. Эта часть синусоиды заштрихована. Вся амплитуда выходного сигнала определяется

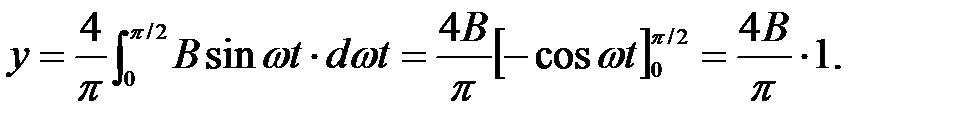
Рис.2.26. Выходной сигнал идеального реле и его первая гармоника

Тогда Г- ФП идеального реле при выходном сигнале В и при амплитуде входного сигнала А

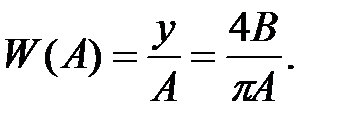
Таким образом, ограничиваясь рассмотрением первой гармоники на выходе нелинейного элемента при гармоническом сигнале на его входе, заданный вид нелинейности заменяют линейным уравнением, которое зависит от амплитуды входного сигнала А. Такая замена называется гармонической линеаризацией нелинейных зависимостей.

Рассмотрим, какие особенности имеет гармоническая передаточная функция при неоднозначной характеристике релейного элемента на примере такого элемента с гистерезисной характеристикой. Определение гармонической передаточной функции (Г-ПФ) нелинейного элемента будем производить при тех же двух условиях (смотри рисунок 2.21):

- на вход НЭ поступает сигнал x(t)= A·sinωt;

- ЛЧ системы обладает свойством фильтра.

Полученное значение выходного сигнала y(t) так же разложим в ряд Фурье и расчет проведём по основной гармонике y(t)=B₁sinωt + С₁cosωt, где B₁ – выходная величина реле, C₁ – характеризует влияние гистерезиса.

Коэффициенты ряда Фурье определяются по формулам

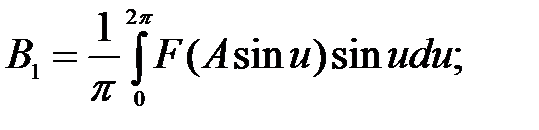
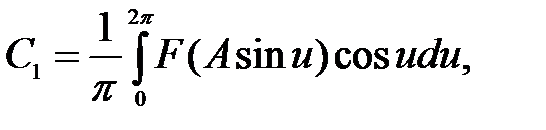
где u – переменная интегрирования, u = ωt.

Учитывая, что x(t) = Asinωt, тогда

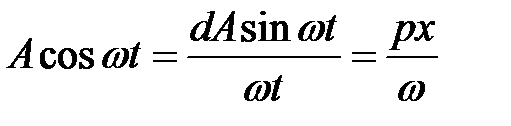
Обозначим отношение выходного сигнала к входному, который задан в виде амплитуды A через q(A) и q^’(A)

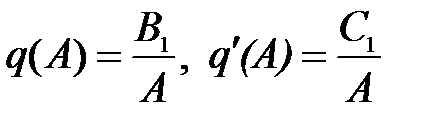
С учетом этих обозначений

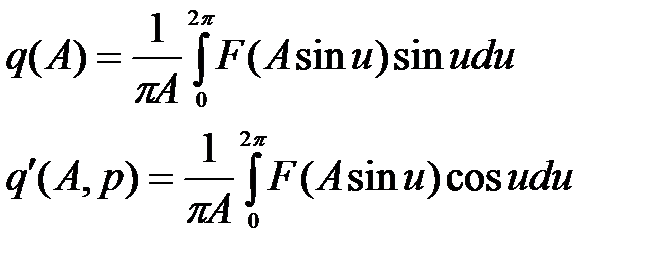
Тогда гармоническая передаточная функция

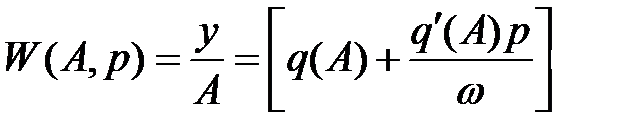
Для определения гармонической частотной передаточной функции сделаем подстановку p = jω

W(A,ω) = [q(A) + jq^’(A)]

Коэффициенты q(A) и q^’(A) называются коэффициентами гармонической линеаризации.

С помощью представления нелинейного элемента в виде гармонической передаточной функции достаточно просто на основании критерия Найквиста можно определить частоту и амплитуду автоколебаний. Этот способ известен в литературе как метод Гольдфарба. Для его использования необходимо предварительно преобразовать схему нелинейной системы так, чтобы все линейные элементы объединились в одну частотную передаточную функцию W_лч(jω). При этом нелинейный элемент представляют в виде гармонической частотной передаточной функции W_нэ(A) на входе системы. Тогда общая передаточная функция системы в разомкнутом состоянии W_раз(jω,A) = W_нэ(A)W_лч(jω).

Предположим, что замкнутая нелинейная система находится на границе устойчивости и в ней возникли незатухающие колебания (автоколебания). Тогда согласно критерию Найквиста амплитудно-фазовая характеристика разомкнутой системы Wраз(j ω,A) должна проходить через точку с координатами (-1, j0). Отсюда условие существования автоколебаний в замкнутой системе:

Wн.э(A)·Wл.ч(jω)· = -1.

Непосредственно построить эту амплитудно-фазовую характеристику на комплексной плоскости трудно. В этом уравнении две переменных величины: частота ω, которую изменяем от 0 до ∞ и амплитуда входного сигнала на нелинейного элемента А, который определяется по Wл.ч(jω). Л.С. Гольдфарб предложил это уравнение представить в виде

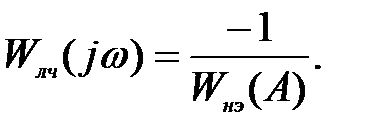
Автоколебания в системе возможны, если выполняются два условия гармонического баланса

.

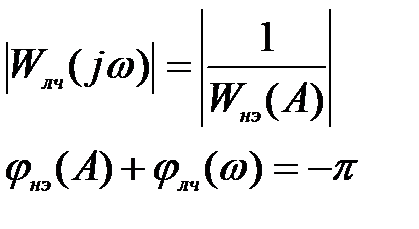Первое условие. Отдельно построенная левая часть уравнения при изменении частоты и отдельно построенная правая часть уравнения при изменении амплитуды имеют общую точку пересечения (в некоторых случаях несколько точек пересечения).

Второе условие. Точки пересечения соответствуют суммарному фазовому сдвигу на угол -π (радиан) или минус 180⁰.

Таким образом, колебательный процесс в системе возможен, если есть точки пересечения амплитудных характеристик и выполняется требование к фазовым характеристикам (рис. 2.27).

Полученные уравнения проще всего решать графо-аналитически. Очевидно, что если эти два годографы на комплексной плоскости не пересекаются, то они не имеют общего решения, и в исследуемой системе нет колебательного процесса (рисунок 2.27 а). Если эти годографы пересекаются, то есть общее решение в исследуемой системе и есть колебательный процесс (рисунок 2.27 б). Если эти годографы пересекаются в двух точках, то в исследуемой системе есть два вида колебательных процесса. Из них один вид или с амплитудой А1 – неустойчивый колебательный процесс, а второй вид или с амплитудой А2 – устойчивый колебательный процесс (рис. 2.28 в).

Рис.2.27. К определению частоты и амплитуды автоколебаний

Об устойчивости или неустойчивости колебательного процесса судят следующим образом. Пусть годографы пересекаются в точке А1 при частоте ω0 и амплитуде А0 (рисунок 2.27 в). Зададим некоторые приращение ΔА. Для устойчивости автоколебаний требуется, чтобы при А1 +ΔА колебания становились затухающие и амплитуда возвращалась к А1. При А1 – ΔА колебания становились возрастающие и амплитуда тоже возвращается к А1.

Если при А1 +ΔА амплитуда начала возрастать, а при А1 – ΔА она стала

убывать, то возникший предельный цикл неустойчивый.

Контрольные вопросы для самопроверки

1. Какой сигнал считается центрированным?

2. Как определяется передаточная функция нелинейного звена?

3. Почему у нелинейного звена передаточная функция называется гармонической?

4. Чему равна передаточная функция нелинейного звена с зоной нечувствительности при A<a?

5. Как получается гармоническая частотная передаточная функция нелинейного звена?

6. Как можно математически через коэффициенты q(A) и q’(A) определить величину запаздывания?

7. С увеличением амплитуды входного сигнала величина запаздывания в нелинейных звеньях с петлей гистерезиса увеличивается или уменьшается?

8. С увеличением частоты входного сигнала величина запаздывания в однозначных нелинейных звеньях увеличивается или уменьшается?