 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекция 2. Типовые нелинейные звенья
|
|
ПОНЯТИЕ О НЕЛИНЕЙНЫХ СИСТЕМАХ
Лекция 1. Особенности процессов в нелинейных системах
План лекции
1. Понятие нелинейной системы
2. Неединственность положения равновесия
3. Конечная длительность процессов
4. Ограниченность уровней переменных
5. Автоколебания
6. Зависимость характера движений
от начальных условий и уровней воздействий
Содержание лекции
Расчет нелинейных систем управления значительно сложнее, чем линейных. Это объясняется большим разнообразием движений, описываемых нелинейными уравнениями. Переход от линейных моделей к нелинейным, т.е. их усложнение ― мера вынужденная. Необходимость расширения и углубления знаний о поведении систем управления в сторону анализа и синтеза нелинейных систем должна быть обоснована.
Напомним, что решение обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами
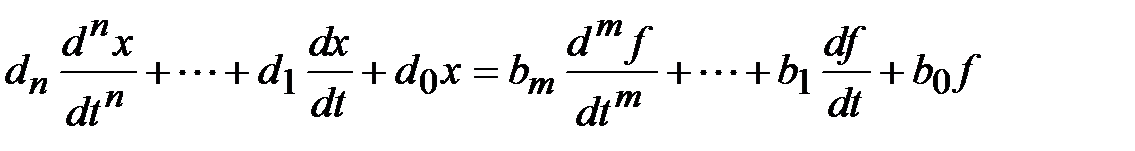 (1.1)
(1.1)
представляется в виде суммы
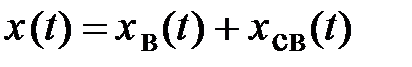 , (1.2)
, (1.2)
где 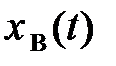 ― частное решение неоднородного уравнения (1.1), описывающее вынужденное движение;
― частное решение неоднородного уравнения (1.1), описывающее вынужденное движение;
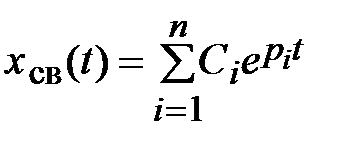 (1.3)
(1.3)
― общее решение соответствующего однородного уравнения, описывающее свободное движение при начальных условиях: 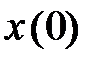 ,
, 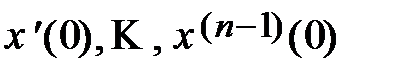 .
.
Выражение (1.3) записано для случая простых корней 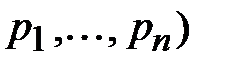 характеристического полинома
характеристического полинома
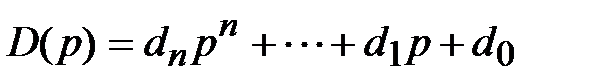 . (1.4)
. (1.4)
Относительная простота анализа линейных моделей объясняется возможностью раздельного анализа вынужденных и свободных движений, а также тем, что известна форма решения (1.3). Построение решения сводится к алгебраическим задачам вычисления корней характеристического полинома и решения системы линейных уравнений относительно коэффициентов Ci.
Вместе с тем разнообразия движений, описываемых линейными уравнениями, может оказаться недостаточным для анализа нелинейных систем. Рассмотрим некоторые из наиболее существенных отличий между процессами в линейной и нелинейной моделях систем автоматического управления.
Неединственность положения равновесия. Линейная система имеет единственное положение равновесия. Например, выходная переменная системы, описываемой уравнением (1.3), при постоянном воздействии f принимает единственное значение, равное
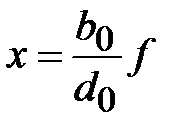 .
.
Если система находится не на границе устойчивости, то при любых начальных условиях движения асимптотически затухают к положению равновесия (система устойчива в целом) или расходятся (система не устойчива).
В качестве примера представим себе следящую систему управления, датчик рассогласования и электродвигатель привода которой имеют зоны нечувствительности. Если рассогласование мало, то напряжение на входе двигателя по модулю меньше напряжения трогания и двигатель не вращается. Положения равновесия системы относительно переменной входа двигателя образуют отрезок, то есть множество значений выходной переменной (положения).
Конечная длительность процессов. Если линейная система устойчива, т.е. корни pi характеристического полинома (1.4) имеют отрицательные действительные части, то соответствующие экспоненты в решении (1.3) затухают в бесконечности. Реально же длительность процессов управления конечна (кривая 1 на рис. 1.1), чему способствуют зоны нечувствительности элементов, сухое трение и люфты (зазоры) кинематических сочленений.

Рис. 1.1. Конечная длительность процессов
Ограниченность уровней переменных. Если линейная система неустойчива, то значения переменных неограниченно растут. Реально уровни переменных всегда ограничены энергетическими, материальными, прочностными ресурсами. На рис. 1.2 непрерывными линиями показаны экспоненциально расходящиеся процессы в линейных системах первого (рис. 1.2, а) и второго (рис. 1.2, б) порядков. Штриховые кривые соответствуют реальным процессам.
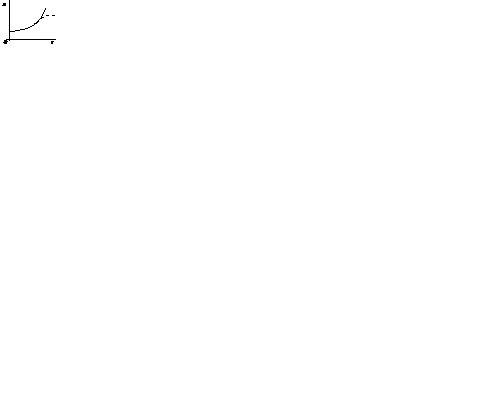
|
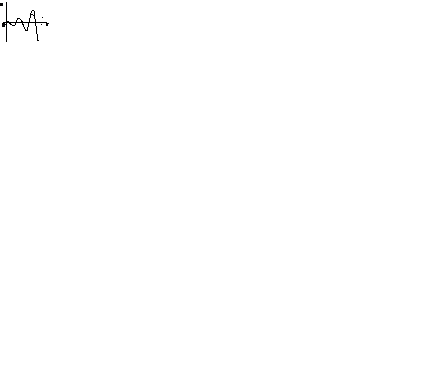
|
Рис. 1.2. Ограниченность уровней переменных
Автоколебания - периодические движения за счет внутренних свойств системы при отсутствии внешних колебательных воздействий. В линейных системах периодические движения гармонической формы соответствуют колебательной границе устойчивости. Амплитуды этих колебаний зависят от начальных условий. При самом незначительном изменении параметров системы колебания превращаются в затухающие или расходящиеся.
Автоколебания имеют относительно стабильную амплитуду и частоту, которые восстанавливаются после снятия возмущений. На рис. 1.2, б штриховая линия соответствует автоколебаниям в системе с неустойчивым положением равновесия.
Зависимость характера движений от начальных условий и уровней воздействий. В реальных системах не выполняется принцип суперпозиции - при сложении воздействий реакция не равна сумме реакций на отдельные воздействия. На рис. 1.3 показаны графики процессов в одной и той же динамической системе (физический маятник) в зависимости от начальных условий.

|
Рис. 1.3. Зависимость процессов от начальных условий
Примеры явлений, не объясняемых теорией линейных систем, можно продолжить.
Нелинейные математические модели, используемые для анализа систем управления, появляются вследствие учета естественных (сопутствующих) эффектов, присущих объекту или элементам системы управления и обусловленных нелинейным характером законов природы, которым подчиняются исследуемые явления. Нелинейности могут вводиться и специально с целью компенсации нежелательных эффектов от естественных нелинейностей или для придания системе управления особых свойств, которые принципиально недостижимы линейными средствами. Так, именно нелинейные алгоритмы управления могут обеспечить максимальное быстродействие процессов при наличии естественных ограничений на уровни управляющих воздействий; нелинейности обязательно вводятся при создании генераторов колебаний и т.д. В ряде систем управления техническими объектами нелинейные, в частности, релейные регулирующие устройства оказываются наиболее простыми, дешевыми и надежными.
Контрольные вопросы для самоподготовки
1. Какая система автоматического управления считается нелинейной?
2. Почему линейную систему анализировать математически проще, чем нелинейную?
3. Как определяется «принцип суперпозиции»?
4. Какие два вида устойчивого состояния имеет нелинейная система?
5. Какие 3 вида устойчивости имеет нелинейная система управления?
6. Что значит система устойчивости «в целом»?
Лекция 2. Типовые нелинейные звенья
План лекции
1. Однозначные нелинейности
2. Многозначные нелинейности
3. Релейные нелинейности
Содержание лекции
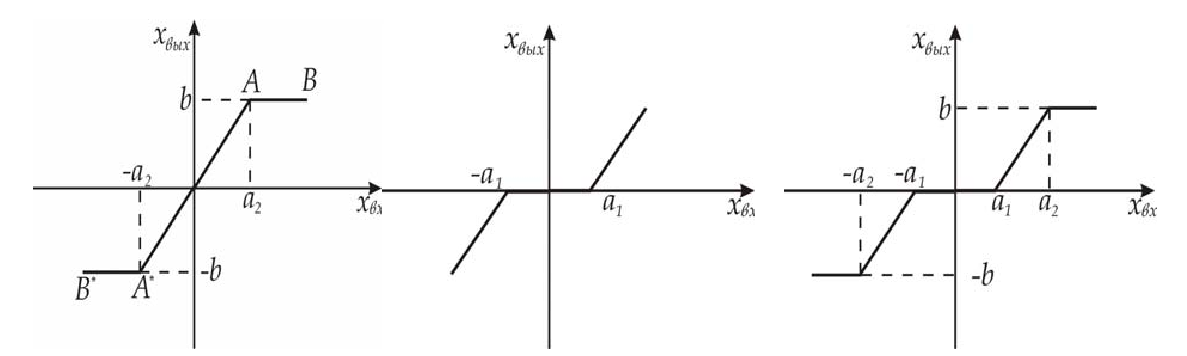
Нелинейные характеристики могут быть разделены на однозначные (рисунок 1.4 а, б, в) и неоднозначные (рисунок 1.5 а, б, в). Рассмотрим типовые кусочно-линейные, однозначные характеристики нелинейных элементов.
a) б) в)
а) - нелинейная характеристика с насыщением;
б) - нелинейная характеристика с зоной нечувствительности;
в) - нелинейная характеристика с насыщением и зоной нечувствительности.
Рис.1.4. Характеристика элементов с однозначной зависимостью
Характеристика, показанная на рисунке 1.4а имеет линейную зону (A* A) и участок насыщения (AB и B*A*). Уравнение такой статической характеристики
xвых = k×xвх при | xвх | ≤ a2 ,
xвых = b×sign(xвх) при | xвх | > a2
Характеристика, показанная на рис.1.4б имеет зону нечувствительности при | xвх |≤ a. Уравнение такой статической характеристики
xвых = 0 при | xвх | ≤ a1,
xвых = k(xвх – a1) при xвх > a1,
xвых = k(xвх+a1) при xвх < –a1.
Характеристика, показанная на рис.1.4в имеет и зону нечувствительности и участок насыщения. Уравнение статической характеристики
xвых = 0 при | xвх | ≤ a1,
xвых = k(xвх – a1) при a2 > xвх > a1,
xвых = k(xвх+a1) при –a2 < xвх < –a1.
xвых = b×sign(xвх) при | xвх | >a2
Рассмотрим неоднозначные кусочно-линейные характеристики нелинейных элементов.
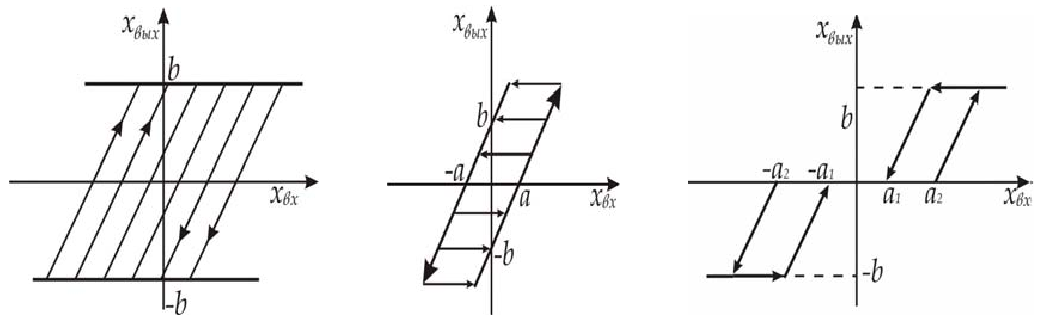
a) б) в)
а) - нелинейная характеристика “упор” для ограничения движения;
б) - нелинейная характеристика “люфт” без зоны нечувствительности;
в) - нелинейная характеристика “люфт” с зоной нечувствительности.
Рис. 1.5. Характеристика элементов с неоднозначной зависимостью
Характеристика, показанная на рис.1.5 a показывает ограничения типа «упор» в зависимости от направления движения входного сигнала. Уравнение такой характеристики
xвых=b при x’вх > 0,
xвых=b при x’вх < 0.
Характеристика, показанная на рис.1.5 б имеет зону неоднозначности и участок насыщения xвых = | b |. Это гистерезисная характеристика типа «люфт». Уравнение такой характеристики
xвых = k(xвх – a) при xвх > 0,
xвых = k(xвх+a) при xвх < 0
xвых = b×sign(xвх) при | xвх | = 0.
Характеристика, показанная на рис.1.5 в дополнительно имеет зону нечувствительности. Уравнение такой характеристики
xвых = 0 при | xвх | <a1
xвых = k(xвх – a) при xвх > 0,
xвых = k(xвх+a) при xвх < 0
xвых = b×sign(xвх) при xвх = 0.
Если в системе есть элемент с релейной характеристикой, то такая системы называется релейной или дискретной системой, в которой релейный элемент осуществляет квантование сигнала по уровню.
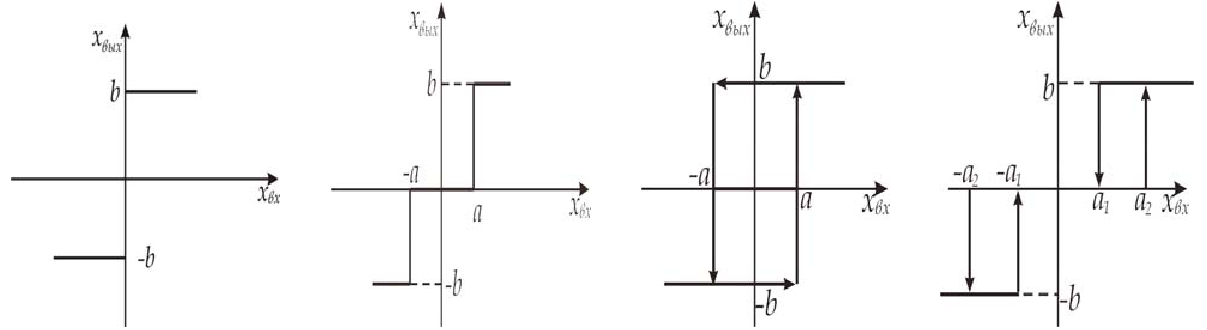
a) б) в) г)
а) - характеристика идеального реле;
б) - характеристика реле с зоной нечувствительности;
в) - характеристика реле с гистерезисом;
г) - характеристика реле с зоной нечувствительности и гистерезисом.
Рис.1.6. Характеристики реле
Характеристика, показанная на рис.1.6а – это идеальное двухпозиционное реле.
xвых = b×sign(xвх)
Характеристика, показанная на рис.1.6.б – это трехпозиционное реле, в котором дополнительная позиция появляется за счет нечувствительности. Уравнение такой характеристики
xвых = 0 при | xвх | <a
xвых = b×sign(xвх) при | xвх | > a.
Характеристика, показанная на рис.1.6в – это двухпозиционное реле с гистерезисом. Его еще называют «реле с памятью». Оно «помнит» свое предыдущее значение и в пределах | xвх | <a сохраняет это свое значение. Уравнение такой характеристики
xвых = b×sign(x – a) при x’вх > 0,
xвых = b×sign(x + a) при x’вх < 0,
xвых = +b при xвх > – a; x’вх < 0,
xвых = – b при xвх < a; x’вх > 0.
Характеристика, показанная на рис.1.6г – это трехпозиционное реле с гистерезисом, в котором дополнительная позиция образована за счет зоны нечувствительности. Уравнение такой характеристики
xвых = b/2[sign(x – a2) + sign(x + a1)] при x’вх > 0,
xвых = b/2[sign(x + a2) + sign(x – a1)] при x’вх < 0.
Из приведённых уравнений видно, что при отсутствии петли гистерезиса выходное воздействие реле зависит только от значения xвх или xвых = f (xвх). При наличии петли гистерезиса значение xвых зависит ещё и от производной по xвх или xвых = f(xвх, x’вх), где x’вх характеризует наличие “памяти” у реле.
Контрольные вопросы для самоподготовки
1. Отличие однозначной и многозначной характеристики
2. Какая характеристика называется четно-симметричной?
3. Какая характеристика называется нечетно-симметричной?
4. Какое реле называют реле с памятью?
Дата публикования: 2015-09-17; Прочитано: 4403 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
