Лекция 4. Фазовые портреты линейных систем

План лекции

1. Типы звеньев, описываемых линейным дифференциальным уравнением второго порядка

2. Фазовые портреты колебательных звеньев

3. Фазовые портреты апериодических звеньев

4. Типы особых точек фазовых портретов линейных систем

Содержание лекции

Фазовые портреты нелинейных систем в окрестности особых точек близки к фазовым портретам линеаризованных систем. В связи с этим рассмотрим особенности фазовых портретов и особых точек линейных систем второго порядка, в зависимости от расположения корней характеристического полинома.

Пусть переходный процесс в некоторой системе описывается уравнением второго порядка:

.

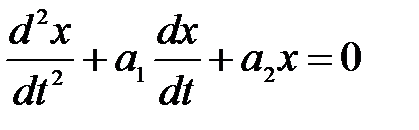Введем обозначение для скорости изменения отклонения управляемой величины y=dx/dt. Тогда уравнение второго порядка преобразуется к системе уравнений в форме Коши:

.

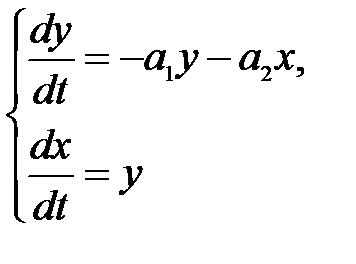Исключим из последних уравнений время t, разделив первое из них на второе

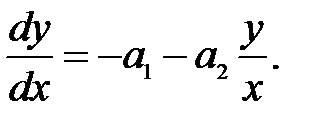
Решение y = φ(x) этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (x,y) каждая из которых соответствует одному определенному значению произвольной постоянной.

Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в данной системе при любых начальных условиях.

Рассмотрим отдельно различные случаи. Корни характеристического уравнения рассматриваемой системы

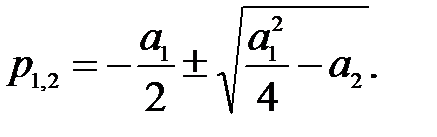
Возможны шесть случаев расположения этих корней на комплексной плоскости:

1) корни чисто мнимые при a₁ = 0, a₂>0 (колебательная граница устойчивости линейной системы);

2) корни комплексные и имеют отрицательные вещественные части при

a₁² < 4a₂, a₁ > 0, a₂ > 0 (устойчивая линейная система);

3) корни комплексные и имеют положительные вещественные части

при a₁² < 4a₂, a₁ < 0, a₂ > 0 (неустойчивая линейная система);

4) корни вещественные отрицательные при a₁² < 4a₂, a₁ < 0, a₂ > 0 (устойчивая линейная система);

5) корни вещественные положительные при a₁² < 4a₂, a₁ < 0, a₂ > 0 (неустойчивая линейная система);

6) корни вещественные и имеют разные знаки при a₂ < 0 (неустойчивая линейная система); в частности, один из корней будет равен нулю при a₂ = 0 (апериодическая граница устойчивости линейной системы).

В первом случае получаются, как известно, незатухающие колебания (рис.2.1)

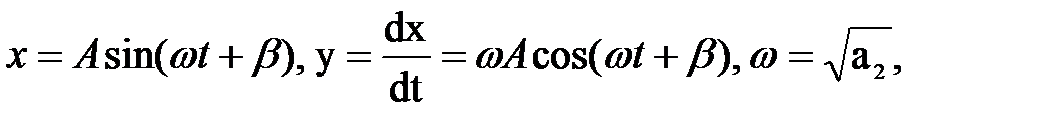
с постоянной амплитудой A и начальной фазой β, которые зависят от начальных условий. Для фазовой плоскости последние уравнения представляют собой параметрические уравнения эллипса с полуосями A и ωA (см.рис.2.3). Уравнение эллипса

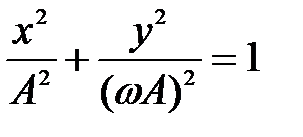
можно получить непосредственно решением дифференциального уравнения фазовых траекторий при a₁ = 0 и a₂ = ω², причем A – произвольная постоянная интегрирования.

Рис.2.3. Фазовый портрет консервативного звена

Итак, периодическим колебаниям системы соответствует движение изображающей точки по замкнутой кривой (см.рис.2.3).

Во втором случае (комплексные корни с отрицательными вещественными частями), как известно, имеют место затухающие колебания

(рис. 2.4)

,

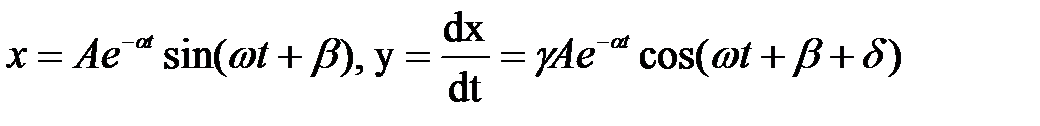где

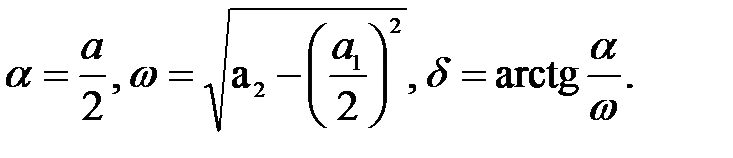
Произвольные постоянные A и β определяются из начальных условий:

x = x₀, y = y₀ = dx₀/dt при t = 0.

Рис.2.4. Фазовый портрет устойчивого колебательного звена

Значения x и у не возвращаются за период колебания к прежним, а становятся меньше. Это дает на фазовой плоскости (x, y) кривую (см.рис.2.4), которая за один оборот не возвращается в прежнюю точку, а подходит ближе к началу координат.

Итак, затухающим колебаниям системы отвечают фазовые траектории в виде спиралей, по которым изображающая точка приближается к началу координат (см.рис.2.4).

В следующем случае (комплексные корни с вещественными частями большими нуля) переходный процесс соответствует расходящимся колебаниям (рис.2.5). Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траекторий тоже в виде спиралей, но только изображающая точка будет двигаться по ним не к началу координат, а от него.

Рис.2.5. Фазовый портрет неустойчивого колебательного звена

В четвертом случае (вещественные отрицательные корни) переходный процесс соответствует уравнениям

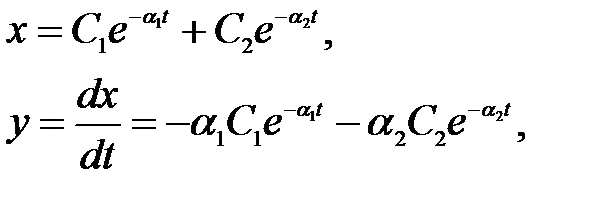
где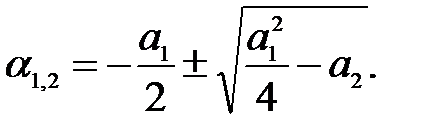

На рис.2.6 показаны три возможных варианта протекания такого процесса.

Рис.2.6. Фазовый портрет устойчивого апериодического звена

Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.

Пятый случай (вещественные положительные корни) соответствует также апериодическому процессу, определяемому теми же уравнениями (7), но при a₁ < 0 и a₂ <0. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 2.7.

В шестом случае (вещественные корни разных знаков) также имеет место апериодический процесс (7) (рис.2.8.), где α₁ и α₂ имеют разные знаки, но картина фазовых траекторий здесь иная. Так как α₂<0, то введем обозначение α² = - a₂, причем для простоты построений рассмотрим случай a₁ = 0, что соответствует согласно (3) уравнению системы dy/dt – α²x = 0 и согласно (5) – уравнению фазовых траекторий

Рис.2.7. Фазовый портрет неустойчивого апериодического звена

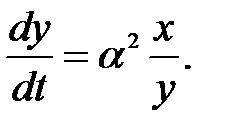
Интегрирование этого уравнения аналогично случаю 1 дает

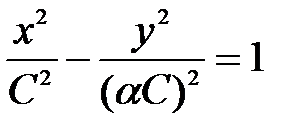
т.е. семейство гипербол, изображенное на рис.2.6.

Направления движения изображающей точки M по фазовым траекториям, показанные на рис.2.6, легко определяются в каждой четверти плоскости по знаку dy / dx (8).

Аналогичная картина фазовых траекторий получится в данном случае и при a₁ ≠ 0.

Рис.2.8. Фазовый портрет звена с отрицательным статизмом

Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории типа рис.2.7 или типа рис.2.8, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.

В целом фазовые портреты линейных систем могут быть следующих видов:

а) центр, когда корни характеристического уравнения мнимые, сопряженные;

б) устойчивый фокус, когда корни характеристического уравнения комплексные, сопряженные, с отрицательной вещественной частью;

в) неустойчивый фокус, когда корни характеристического уравнения комплексные, сопряженные, с положительной вещественной частью;

г) устойчивый узел при вещественных отрицательных корнях;

д) неустойчивый узел при вещественных положительных корнях;

е) седло при вещественных корнях разных знаков.

Рассмотренные фазовые портреты линейной системы второго порядка показывают, что по характеру фазовых траекторий можно непосредственно судить об устойчивости движения системы и об её динамической характеристике. Нелинейные элементы искажают характер фазовых траекторий. Но в принципе эти траектории имеют такой же вид, такое же название и такую же зависимость от корней характеристического уравнения. По фазовому портрету нелинейной системе так же можно анализировать её динамическую характеристику.

Контрольные вопросы для самоподготовки

1. При каком значении демпфирования в колебательном звене фазовый портрет имеет вид устойчивого предельного цикла?

2. При каком значении демпфирования в колебательном звене фазовый портрет имеет вид устойчивого фокуса?

3. При каком значении демпфирования в колебательном звене фазовый портрет имеет вид неустойчивого фокуса?

4. При каком значении демпфирования в звене фазовый портрет имеет вид устойчивого узла?

5. При каком значении демпфирования в звене фазовый портрет имеет вид неустойчивого узла?

6. При каком значении демпфирования в звене фазовый портрет имеет вид седла?