Применение закона Гаусса для расчёта электрического поля системы проводников

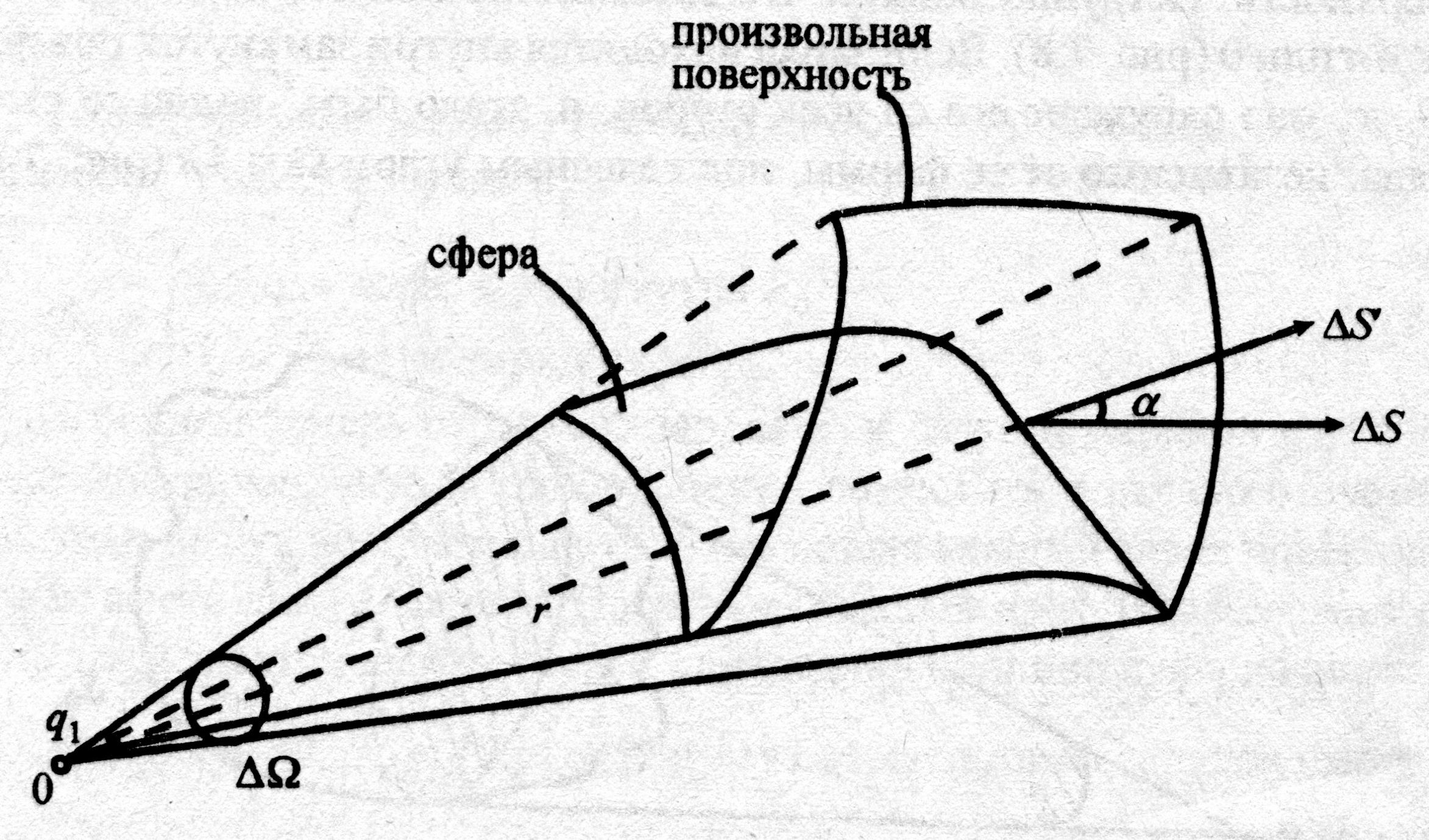
Рис. 9.7. Применение закона Гаусса-Остроградского для поверхности произвольной формы

DS¢

Полученные в предыдущем параграфе результаты, формула (9.11), обобщим теперь на замкнутую поверхность произвольной формы. Вычислим для этого элемент потока DN_E вектора напряжённости 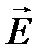через элемент этой произвольной поверхности DS (рис. 9.7.), определяемой радиус-вектором 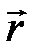. Поскольку нормаль к произвольной поверхности (рис. 9.7) не совпадает с направлением вектора напряжённости, пронизывающего поверхность сферы, поток силового поля неподвижного заряда будет находиться через скалярное произведение:

DN_E = (E × DS) = E × DS ×cosa. (9.12)

Почему? Здесь DS ×cosa (см. рис. 9.7.) – это проекция элемента площадки DS произвольной поверхности на элемент DS ¢ сферы радиуса 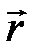с центром в точке расположения электрического заряда q ₁. Подставляя в формулу (9.12) выражение вектора напряжённости для точечного заряда q ₁ из (9.4), для элемента потока DN_E получаем:

DN_E = . (9.12 а)

Ранее, в работе [3, с. 13] мы убедились в том, что при малых линейных углах отношение длины дуги к радиусу, образующему эту дугу, отражает значение этого угла, т. е. Dj @ Ds/ R. Естественно ожидать, что элементарная площадка DS ¢ = DS ×cosa опирается на телесный угол 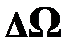, см. рис. 9.7, а его численное значение может быть представлено 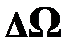= = DS ¢ / r ² = DS ×cosa / r ². Подставляя это в формулу (9.12 а), для элемента потока на сфере радиуса 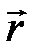получаем:

DN_E = k × q ₁× 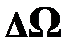. (9.13)

Иными словами, для одного заряда элемент потока электрического поля DN_E через произвольно ориентированный элемент поверхности DS зависит не только от величины заряда, но и от того телесного угла 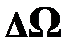, под которым этот элемент поверхности виден из точки, в которой находится заряд.

Для потока N_E через произвольную замкнутую поверхность соответственно имеем уравнение вида:

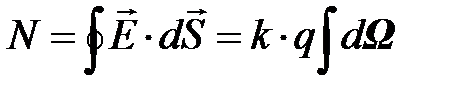, (9.14)

где W – полный телесный угол, под которым видна окружающая заряд q ₁ поверхность. Очевидно, если заряд находится внутри замкнутой поверхности S, то она окружает его со всех сторон и видна со стороны заряда, независимо от её формы, под телесным углом W = 4p стерадиан (семечко «видит» поверхность яблока под углом 4p Ср.).

Перейдём от одного заряда к системе зарядов q_i. Разумеется, все заряды одновременно поместить в начало отсчёта нельзя. Теперь это и не нужно, поскольку охватывающая каждый заряд поверхность может быть любой. Каждый заряд создаёт своё поле Е_i, а поскольку для электрического поля Е справедлив принцип суперпозиции, его поток аддитивен, т.е. N_E = 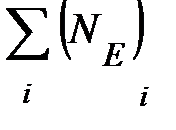. Поэтому поток системы зарядов имеет вид:

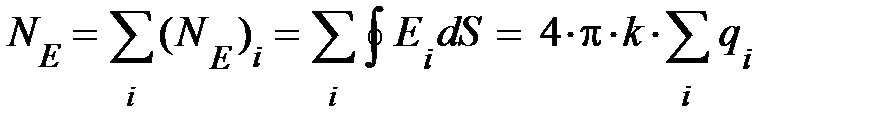, (9.15)

при этом алгебраическая сумма справа распространяется лишь на заряды, расположенные внутри поверхности S.

Формула (9.15) выражает собой закон Гаусса-Остроградского: для произвольной системы неподвижных зарядов поток вектора напряжённости электрического поля через произвольную замкнутую поверхность пропорционален величине электрического заряда, заключённого внутри этой поверхности. Этот же закон для непрерывно распределённых зарядов принимает вид:

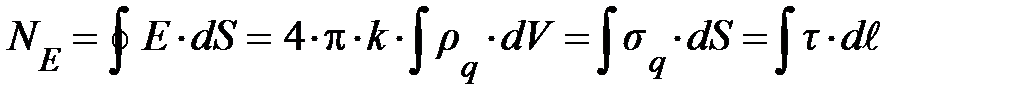; (9.16)

здесь, соответственно, r_q – объёмная плотность электрического заряда, равная q / V; s_q – поверхностная плотность электрического заряда, равная q / S; t – линейная плотность электрического заряда, равная q / .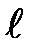

Приведённые здесь рассуждения указывают на то, что поток поля сам по себе не отражает все свойства поля и тем самым ограничивает применение закона Гаусса необходимостью привлекать дополнительно соображения симметрии.

Рассмотрим пример вычисления вектора напряжённости E электрического поля сферы радиуса R, заряженной по объёму с плотностью r_q = const (рис. 9.8).

Решение: Если сфера заряжена положительно, силовые линии направлены как внутри, так и вне сферы по радиусу от центра; это следует из соображений симметрии. Поскольку вычисление потока 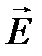не «чувствительно» к форме поверхности, через которую следует вычислять поток, для простоты выберем сферу радиуса r с центром в точке распределения зарядов (рис. 9.8).

Рис. 9.8. Вычисление вектора напряжённости Е сферы, заряженной по объёму

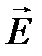Внутри сферы, когда r < R, поток вектора запишется N_E = = Е × S = 4p k ×D q (r) (9.15), где D q (r) – доля заряда, оказавшаяся внутри поверхности сферы интегрирования r < R; её придётся выражать через полный заряд q сфер R. Заряд D q (r) через плотность r_q запишется D q (r) = r_q × 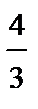×p× r ³; найдём r_q через полный заряд сферы с радиусом R. Пусть этот заряд равен q, тогда r_q = = q / 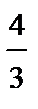×p× R ³, отсюда немедленно следует, что D q (r) = r_q × 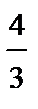×p× r ³ = (q / 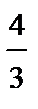×p× R ³)× 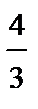×p× r ³ = (q × r ³) / R ³. Подставим это в поток поля формулы (9.15), N_E = = Е × S = 4p k ×D q (r) = 4p k ×(q × r ³) / R ³.Отсюда следует: Е = 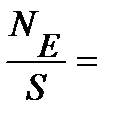= 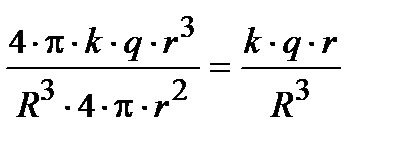. Умножив числитель и знаменатель на 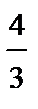×p и приняв к сведению, что q / 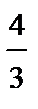×p× R ³ равно плотности заряда сферы r_q, пытливый читатель получит выражение напряженности поля Е = 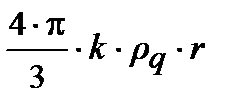внутри сферы радиуса r < R. Проделали? Результатом является вывод – поле внутри сферы зависит от радиуса линейно; можно построить график Е (r); r изменяется от нуля до R.

Настойчивый читатель может самостоятельно найти выражение для вектора напряжённости 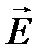на поверхности сферы r > R, проведя такие же рассуждения; это позволит продолжить график от r = R и более, r > R.