Поток вектора напряжённости. Закон Гаусса. Графическое отображение электрического поля

До сих пор обсуждение свойств электрического поля проводилось на основе известных свойств ньютоновских сил взаимодействия зарядов. Чтобы двинуться далее в изучении специфических свойств электрического поля, предпримем усилия по его графическому представлению.

Как и любое векторное поле, электрическое поле 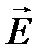можно качественно описать с помощью системы линий поля – силовых линий. Почему? Силовой характеристикой поля является вектор напряжённости и для точечного положительного заряда q, формула (9.4), его модуль запишется: Е = = k × q / r ². Отсюда немедленно следует, модуль вектор 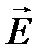быстро уменьшается с увеличением

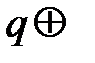
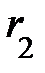
Рис. 9.2. Отображение электрического поля с помощью стрелок

расстояния r (рис. 9.2). Сила взаимодействия между зарядами q и q _o, а вместе с этим и модуль вектора Е направлены вдоль прямой, соединяющей заряды. Естественно, в разных точках r_i этой прямой модуль вектора Е может быть отображён стрелкой с уменьшающейся длиной (рис. 9.2); так как её длина (модуль Е) убывает обратно пропорционально r_i ². Таким образом, качественно электрическое поле может быть отображено с помощью распределения в пространстве системы «стрелок». Вместе с тем, соединяя эти точки, получим линию, силовую, «убегающую» в бесконечность. 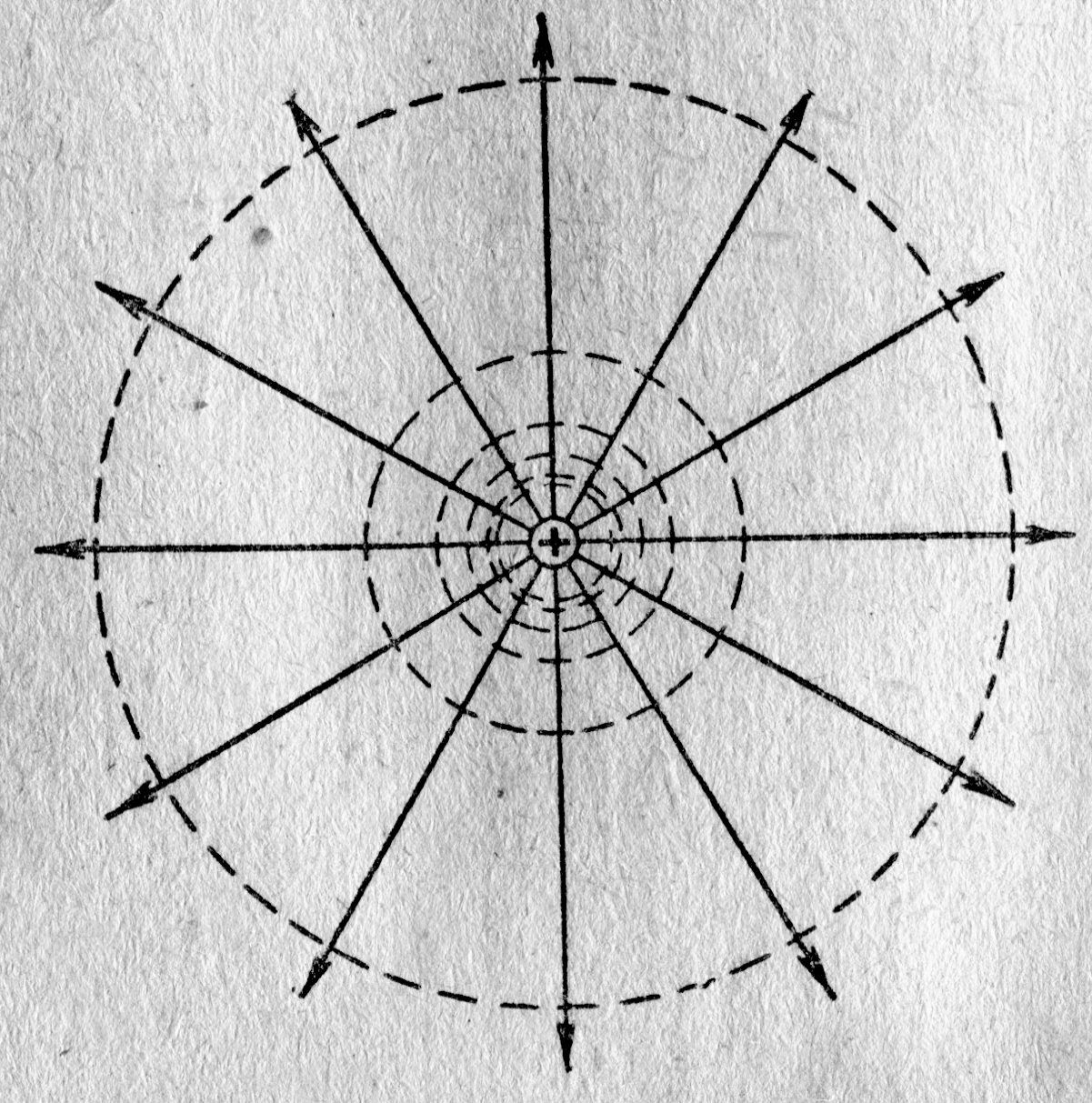В простейшем случае вида (9.4) и с учётом однородности электрических свойств пространства получим сферически симметричную картину силовых линий поля (рис. 9.3). Поскольку электростатическое поле исследуется посредством пробного положительного заряда q _о, принято считать, что силовые линии направлены от заряда, если заряд q > 0, и к заряду, если q < 0. Ещё раз вспомним, силовое поле на рис. 9.3 сферически симметрично (ёжик защищается).

Рис. 9.4. Эквипотенциальные поверхности и силовые линии точечного заряда + q

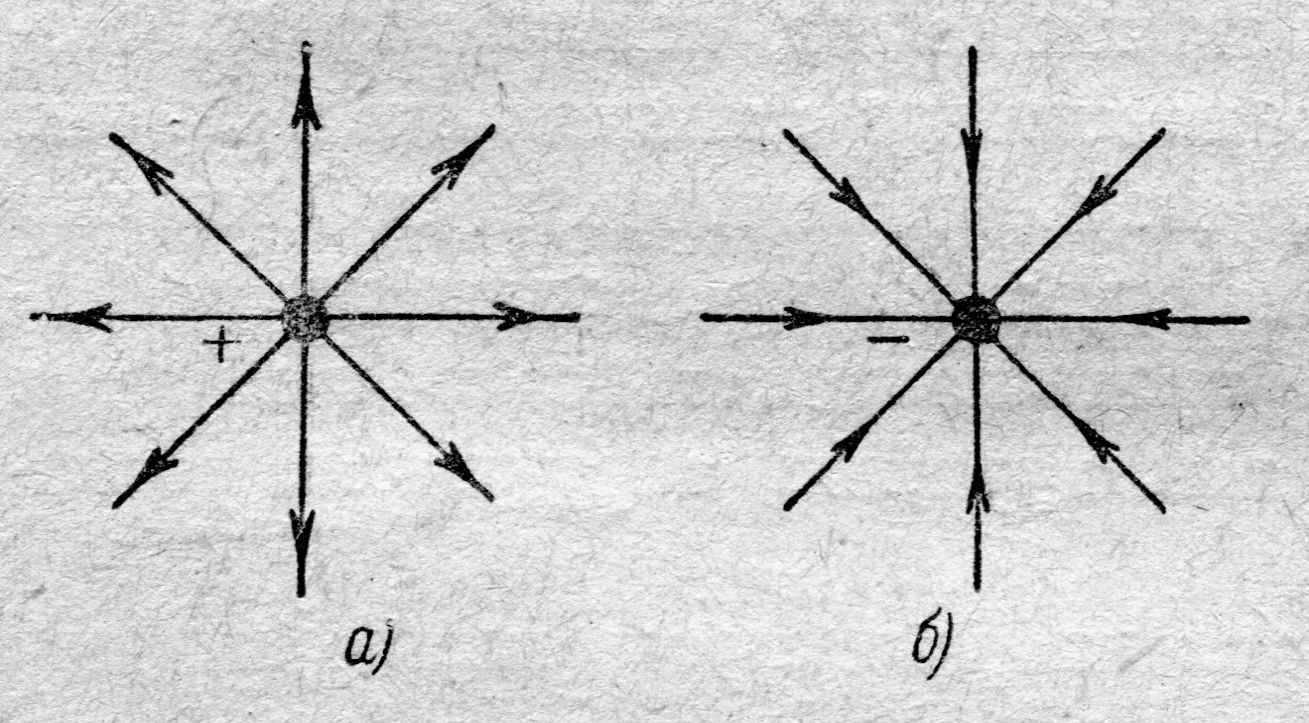
Рис. 9.3. Силовые линии положительно и отрицательно заряженных частиц

Перейдём к графическому представлению электрического поля через его скалярную характеристику «потенциал». Для одного заряда q, помещённого в некоторую точку пространства, электрический потенциал, согласно формуле (9.10), принимает вид: j (r) = k × q / r. Потенциал электрического поля равен работе по перемещению единичного заряда (рис. 9.4) из бесконечности () в точку поля с некоторой координатой r, равноудалённой от положительного заряда; этого требует аналитическое выражение (9.10). С учётом сферической симметрии свойств пространства мы получаем поверхность одинакового потенциала (эквипотенциальные) в виде сферы. Иными словами, пробному электрическому заряду «безразлично», в какой точке на этой поверхности он находится; а именно, воздействие на него электрического поля положительного заряда + q везде одинаково (рис. 9.4).

Эквипотенциальную поверхность можно провести через любую точку поля. Однако условились проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была одна и та же. Это позволяет по густоте эквипотенциальных поверхностей судить о величине силового поля (рис. 9.4); при приближении к заряду эквипотенциальные поверхности становятся гуще, напряжённость поля |D j /D r |, формула (9.7), увеличивается. Пытливый и настойчивый читатель в этом может убедиться, воспользовавшись уравнением (9.10) для единичного заряда q. При записи D j потенциал желательно выразить через r_i, а приращение D r_i, определяющее r _(i+1)-й радиус эквипотенциальной поверхности, будет задавать постоянство разности потенциалов ближайших эквипотенциальных поверхностей. Спрашивайте.

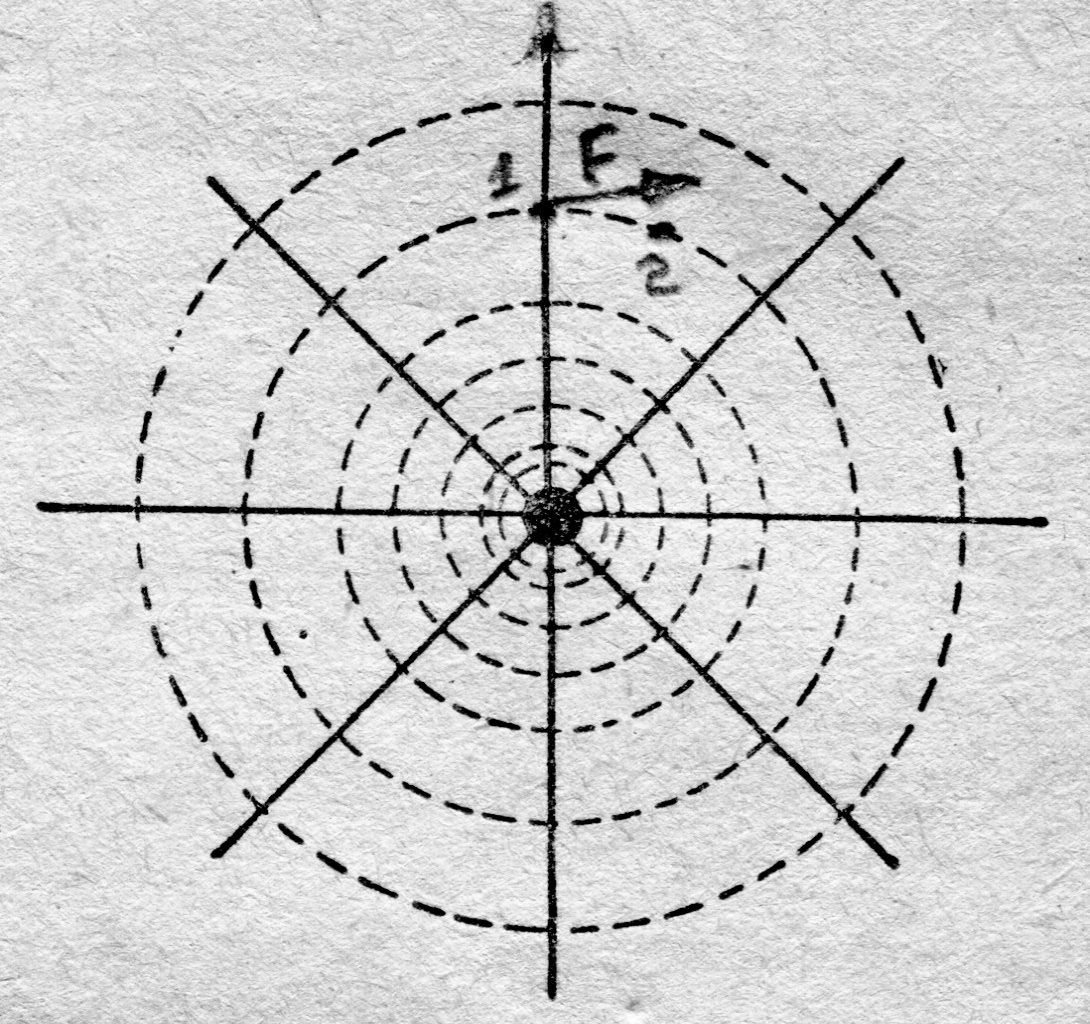
Рис. 9.5. К вопросу о взаимном расположении векторного и скалярного полей неподвижных зарядов

Проясним вопрос взаимного расположения силовых линий электростатического поля и эквипотенциальных поверхностей. На первый взгляд силовые линии должны быть перпендикулярны эквипотенциальным поверхностям, а графическое представление векторного и скалярного j полей (рис. 9.4) не противоречит такому предположению.

Пусть в поле заряда q совершается работа по перемещению пробного заряда q _о из точки 1 в точку 2 (рис. 9.5.). Вспомним, при выводе уравнения (9.7) мы воспользовались тем, что по определению элементарная работа: dA = = F × dS ×cos a. Проецируя это уравнение на электростатическое поле, dA = = q _о× Е × dS ×cos a. Вместе с тем, элементарная работа может быть записана через изменение потенциальной энергии dW, взятой с противоположным знаком, т. е. dA = – dW = = – q _о× dj. Приравнивая между собой правые части уравнений для элементарной работы, получаем выражение: q _о× Е × dS ×cos a = q _о× dj. Левую и правую части выражения можно сократить на q _о, а приняв во внимание, что перемещение осуществляется по поверхности одинакового потенциала, т. е. dj = 0, приходим к уравнению вида: Е × dS ×cos a = 0. Равенство нулю выполняется только в том случае, если cos a = 0, что возможно при a = 0. Таким образом, векторное и скалярное поля неподвижных зарядов взаимно перпендикулярны.

Итак, графическое отображение силового электрического поля неподвижных зарядов стимулировало появление понятия силовой линии. Усилия по отображению скалярного (потенциального) поля привели нас к мысли, что густота эквипотенциальных поверхностей позволяет судить о величине силового поля (с. 135). Таким образом, через силовые линии мы можем судить не только о направлении поля заряда, но и о его величине. Иначе говоря, в безвихревом, потенциальном поле появляется новая характеристика, связанная как-то с числом силовых линий, пронизывающих некую замкнутую поверхность S, охватывающую электрические заряды. Так появляется ещё одна характеристика поток электрического поля неподвижных зарядов, которая на символическом языке (аналитически) может быть записана из следующих соображений.

Для простоты прежде начнём рассмотрение поля одного заряда q (рис. 9.6). Из формулы (9.4) следует, модуль вектора напряжённости 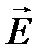электрического поля при r = const постоянен, а распределение его сило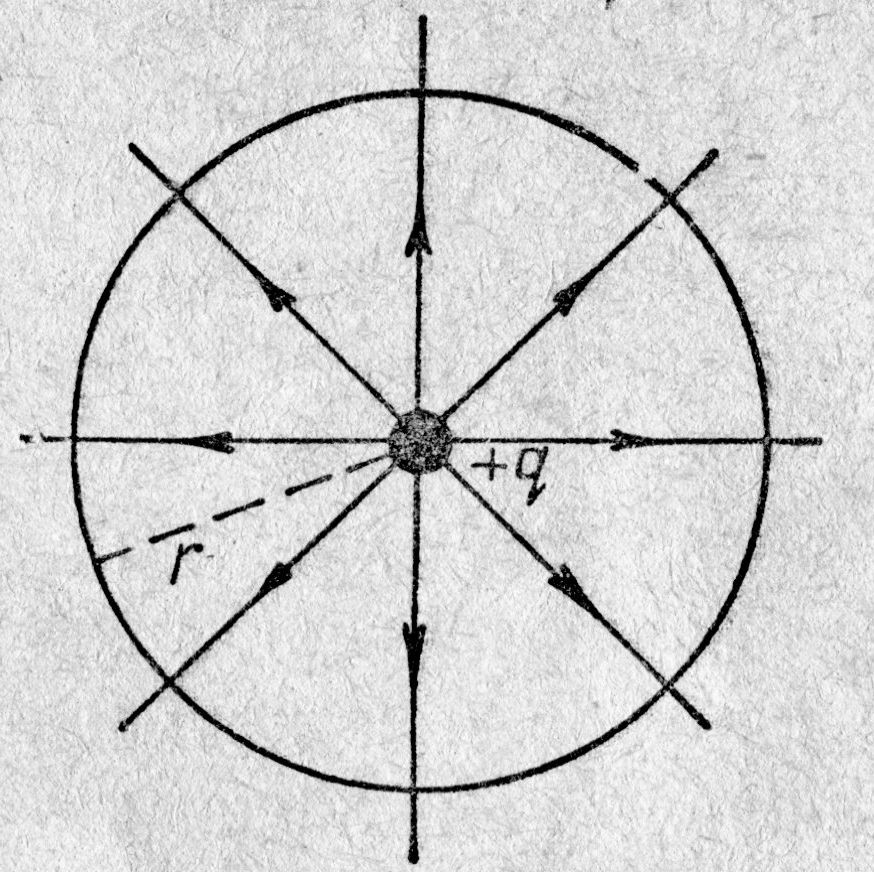

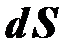
Рис. 9.6. К выводу закона Гаусса-Остроградского.

вых линий, на основании свойств пространства, обладает сферической симметрией. Охватим заряд сферической поверхностью, а её центр совместим с положением точечного заряда q (рис. 9.6), что обеспечивает равенство силового поля на этой поверхности радиуса r. Заметим, поверхность охвата заряда может быть любой.

Выделим на поверхности сферы (рис. 9.6, справа) площадку dS, Пронизывающие её силовые линии поля dN образуют элементарный поток электрического поля через эту площадку; иными словами, элементарный поток вектора напряжённости электрического поля. Очевидно, что этот поток определяется числом силовых линий, приходящихся на единицу поверхности, и элементарной площадкой dS. В качестве числа силовых линий, приходящихся на единицу поверхности, может выступать вектор напряжённости электрического поля 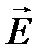; другими словами, формально мы можем некоему значению 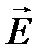присвоить любое, удобное для нас, число силовых линий (1; 4; и т.п.). Итак, мы подошли к тому, чтобы представить на символическом языке поток вектора напряжённости электрического поля неподвижных зарядов. Пусть dN элементарный поток вектора напряжённости электрического поля, а 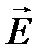число силовых линий, приходящихся на единицу поверхности, тогда элементарный поток поля через площадку dS запишется: 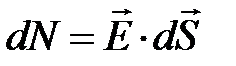. Поскольку формула напряжённости точечного заряда (9.4) известна, а площадь сферической поверхности, охватывающей заряд, после интегрирования (или суммирования) равна 4×p× r ², то выражение для потока электрического поля единичного заряда принимает вид:

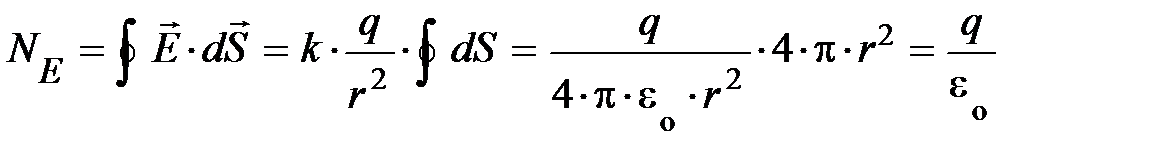. (9.11)

Из формулы (9.11) следует, электрический заряд характеризует интенсивность «источника» электрического поля, а знак заряда определяет и знак источника поля. Другими словами, электрическое поле – это векторное поле с источниками, силовые линии этого поля начинаются и заканчиваются на заряде, а число силовых линий пропорционально величине заряда, характеризующей тенденцию поля к истечению.