Вычисление момента инерции для простейших тел

В предыдущем параграфе было показано, что момент инерции может быть представлен как произведение массы а. т. т. на квадрат эффективного радиуса оси инерции: 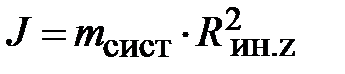. Здесь 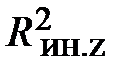, имеющий смысл среднего квадрата расстояния от оси симметрии, может быть представлен в виде: .

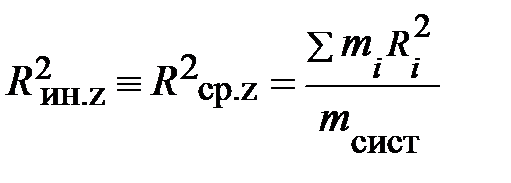В частном случае для системы N частиц с одинаковой массой m_i = m средний квадрат расстояния от оси симметрии может быть представлен следующим образом:

,

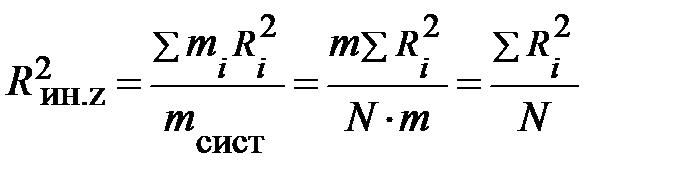и для тонкого обруча радиусом r, когда все R_i = r = const,

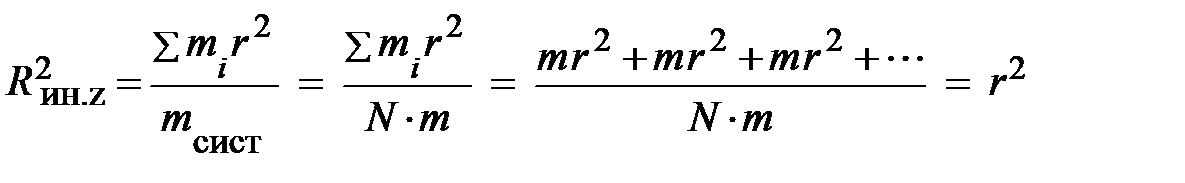. (3.9)

Читателю желательно самостоятельно проделать преобразования, поскольку они требуют сопровождения внутренней речью. В частности, нужно не забыть, что m_i = m и что запись суммы требует произведения массы m на квадрат расстояния r. Убедились в этом самостоятельно? Было бы неплохо тонкий обруч отобразить на рисунке с обозначением заданных величин.

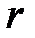
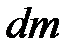
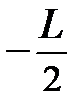
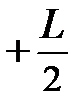
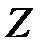
Рис. 3.4. К вычислению момента инерции стержня

Если частицы в а. т. т. распределены непрерывно с плотностью массы r = m / V, то суммирование может быть заменено интегрированием. Убедимся в этом на вычислении момента инерции стержня длиной L относительно оси Z, проходящей через его центр инерции (рис. 3.4), максимальный поперечный размер стержня во много раз меньше длины стержня. Момент инерции J _z запишется:

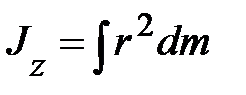, (3.10)

где dm – элементарная масса стержня, удалённая от оси вращения Z на расстояние r и обладающая моментом инерции dJ = r ²× dm. Поскольку плотность материала стержня r одинакова по всей длине, элементарная масса может быть записана: dm = r × dV = r×S×dr; здесь S – площадь поперечного сечения стержня, а dr – длина бесконечно малого элемента стержня массой dm. Подставляя эти значения в уравнение (3.10) приходим к выражению: 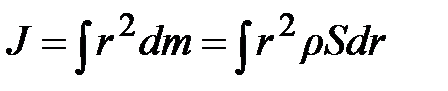. Вынося постоянные r и S из под знака интеграла, приходим к интегралу простейшего вида: 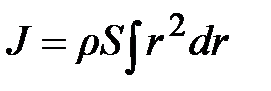. Как следует из рис. 3.4, пределы интегрирования изменяются от – L /2 до + L /2 (?!) и тогда момент инерции стержня запишется:

.

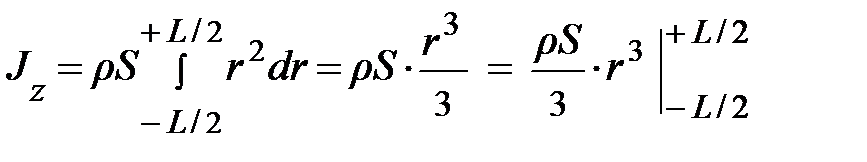Проведя несложные преобразования, пытливый читатель приходит к уравнению вида: 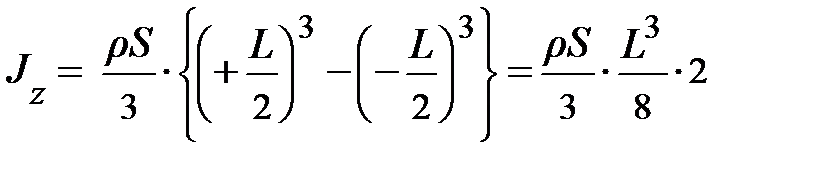. Наконец, приняв к сведению, что r×S×L = m, настойчивый читатель приходит к тому, что относительно оси центра масс Z момент инерции стержня J _z = (1/12)× m×L ². Самостоятельно преобразования проделали?

Рис. 3.5. К вычислению момента инерции для мгновенной оси Z /.

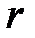
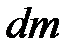
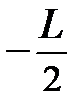
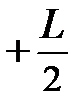
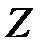
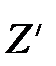Описание свободного вращения стержня можно упростить, воспользовавшись тем, что угловая скорость w _сист.z, будучи общей для всех элементарных масс, не зависит от параллельного переноса оси вращения. Допустим, что наш стержень свободно вращается вокруг оси симметрии Z, проходящей через центр инерции с угловой скоростью w _Z. Рассмотрим теперь его вращение вокруг мгновенной оси Z ^/, параллельной оси Z
(рис. 3.5). В этом случае мы, по существу, имеем дело с комбинацией двух движений – «чистого» вращения вокруг оси Z, характеризуемого моментом импульса L _z = J × w _z, и поступательного движения центра инерции стержня по окружности радиуса R = L /2, где R – расстояние между осями Z и Z ^/, со скоростью u_сист = R × w _z. Сумму кинетических энергий K поступательного движения и вращения системы частиц в этом случае можно представить в виде:

. (3.11)

Входящий в формулу (3.11) эффективный момент инерции J _эф относительно мгновенной оси Z ^/ равен:

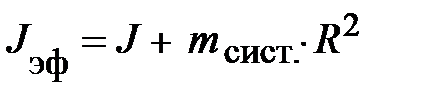, (3.12)

где R – расстояние между осями Z и Z ^/. Формула (3.12) называется формулой Гюйгенса-Штейнера [2] и позволяет вычислять момент инерции для простейших систем. Убедимся в том, что она имеет право на существование. Рассмотрим свободное вращение системы, представленной на рис. 3.5 относительно оси Z ^/. По формуле Гюйгенса-Штейнера эффективный момент инерции J _эф складывается из момента инерции стержня относительно оси его центра масс J _z и момента инерции центра масс стержня по отношению к оси Z ^/. Подставляя в выражение (3.12) заданные параметры, приходим к выражению вида: 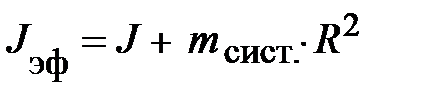. По условию задачи ось вращения Z ^/ удалена от центра масс стержня на половину его длины, т.е. R = L /2, и тогда J _эф = (1/12)× mL ² + m ×(1/2 L)². После несложных преобразований пытливый читатель придёт к выражению J _эф = = (1/3)× mL ². Убедились в этом? Итак, момент инерции стержня относительно оси, проходящей через один из его концов равен одной третьей от произведения массы на квадрат его длины, тогда как относительно оси, проходящей через центр масс всего лишь 1/12 от произведения массы на квадрат длины стержня.

Проверим результат формулы (3.12) J _эф = (1/3)× mL ² через математическую операцию интегрирования. Воспользуемся формулой (3.10), 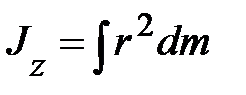и рис. 3.6. Как следует из рис. 3.6, пределы интегрирования изменяются от нуля до L и уравнение (3.10) принимает вид:

.

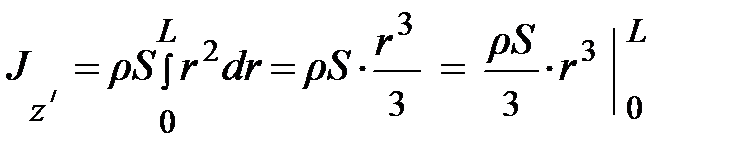Рис. 3.6. К вычислению момента инерции для мгновенной оси Z/

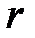
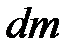
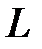
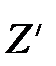Подставив вместо r верхний предел интегрирования L, читатель придёт к выражению:

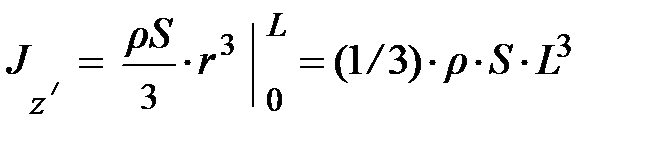. Наконец, учитывая, что rSL = m, приходим к выражению 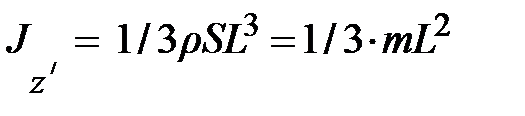, что подтверждает результат, полученный по формуле (3.12).

Применяя дифференциально-интегральное исчисление можно вычислить момент инерции для однородного:

точечного тела, находящегося на расстоянии R от заданной оси вращения J = mR ²;

сплошного шара относительно оси, проходящей через его центр J = (2/5)× mR ²;

полого цилиндра относительно оси, проходящей параллельно его стенкам через центр масс, как разность моментов инерции наружного и внутреннего (отсутствующего) цилиндров J = 1/2 m ₁× R ₁² – 1/2 m ₂× R ₂², или J = 1/2 m ×(R ₁² + R ₂²), где m = m ₁ – m ₂ есть масса полого цилиндра. Для пытливого читателя следует заметить, при попытке получить конечное выражение учтите, что в выражение массы m _i так же входит R_i; может помочь в преобразованиях. Удачи.