Поняття афінного перетворення площини. Група афінних перетворень

Розглянемо відображення 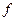, яке кожну точку площини 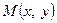переводить у точку 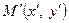та задається співвідношеннями

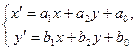, (1)

де матриця 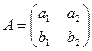вважається не виродженою, тобто 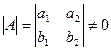. Очевидно, що система рівнянь (1) однозначно розв’язується відносно 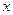та 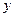, зокрема

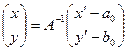. (2)

Тому відображення 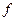, яке різні точки площини переводить у різні, буде перетворенням площини. Перетворення площини, яке задається рівностями (1), називається афінним. Очевидною є вимога невиродженості матриці 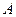. Справді, у випадку 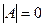система (1) або не мала б розв’язків відносно 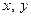, або мала б безліч розв’язків. В обох випадках відображення, задане рівностями (1), не було б перетворенням площини.

Позначимо множину всіх афінних перетворень площини через 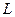та виберемо в ній два перетворення 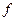та 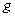, перше з яких задається рівностями (1), а друге – рівностями

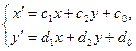, (3)

де 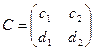- не вироджена матриця.

Нехай при перетворенні 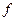точка 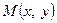перейде у точку 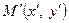, а при перетворенні 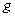точка перейде у точку 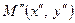. Перетворення, яке точку переводить у точку 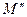назвемо композицією перетворень 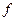та 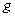. Позначимо операцію композиції символом 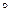та знайдемо рівності, якими визначається відображення 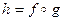. Користуючись спочатку рівністю (3), а потім рівністю (1), дістаємо

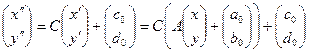
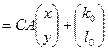, (4)

де 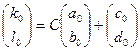. Очевидно, що матриця 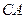не вироджена, оскільки 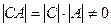. Тому рівність (4) визначає деяке перетворення . Із рівності (2) випливає, що разом із кожним перетворенням 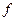множина 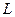містить також обернене до нього перетворення 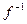. Таким чином пара 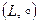є групою. Цю групу називають групою афінних перетворень. Роль нейтрального елемента в цій групі відіграє тотожне перетворення, яке задається рівностями 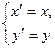. Група афінних перетворень є підгрупою групи перетворень площини.

Розглянемо інший спосіб, яким можна задавати афінні перетворення.

Поряд із деякою афінною системою координат 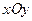, відносно якої розглядається точка 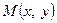та її образ при перетворенні (1) - точка 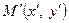, введемо у розгляд іншу систему координат із початком у точці 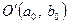та базисними векторами 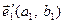та 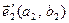, які є лінійно незалежними, оскільки 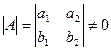. Знайдемо координати точки у новій системі координат 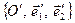. Нехай координатами точки є числа 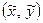, тобто

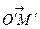
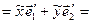
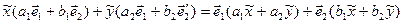. (5)

З рівності 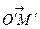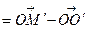дістаємо також співвідношення

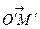
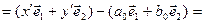
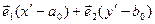. (6)

Порівнюючи (5) та (6), дістаємо

.

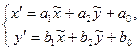Одержана рівність та співвідношення (1) обґрунтовують той факт, що 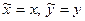. Таким чином, образ точки 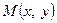при перетворенні (1) у новій системі координат 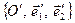має такі самі координати, як і точка . Одержаний факт дозволяє, крім формул (1), задавати афінні перетворення наступним чином.

На площині вибираються дві довільні афінні системи координат (репери) і після цього точці, яка має відносно однієї із систем певні координати ставиться у відповідність точка із такими ж координатами, але уже відносно другого репера. Побудоване таким чином відображення є афінним перетворенням.

Оскільки визначник матриці 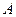афінного перетворення відмінний від нуля, то він може бути додатнім або від’ємним у залежності від того, однаково, чи ні орієнтовані базиси 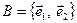та 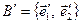. Нехай на площині зафіксовано репер .

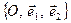Афінне перетворення, для якого перехід до нового репера 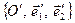здійснюється за допомогою матриці 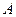, для якої 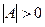, називають власним.

Якщо 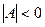, то афінне перетворення називають невласним.

Оскільки для тотожного перетворення 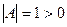, то воно є власним перетворенням. Очевидно, що множина власних перетворень утворює групу, яка є підгрупою групи афінних перетворень. Множина невласних перетворень групу не утворює хоча б тому, що не містить тотожного перетворення.