 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поняття перетворення площини. Приклади перетворень площини
|
|
Лекція 26. Перетворення площини
План
Поняття перетворення площини. Приклади перетворень площини.
Група геометричних перетворень та її підгрупи.
Композиції деяких геометричних перетворень.
Поняття перетворення площини. Приклади перетворень площини.
Нехай задано дві множини 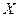 та
та 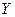 елементів довільної природи. Поставимо певним чином у відповідність кожному елементу
елементів довільної природи. Поставимо певним чином у відповідність кожному елементу 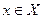 єдиний елемент
єдиний елемент 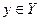 . У цьому випадку говорять, що задано відображення множини
. У цьому випадку говорять, що задано відображення множини 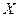 в множину
в множину 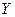 . Позначимо дане відображення через
. Позначимо дане відображення через 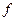 . Той факт, що елемент
. Той факт, що елемент 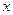 відображається в елемент
відображається в елемент 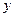 будемо записувати у виді
будемо записувати у виді 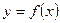 або
або  . При цьому елемент
. При цьому елемент 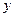 називають образом елемента
називають образом елемента 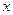 , а елемент
, а елемент 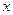 - прообразом елемента
- прообразом елемента 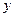 .
.
Множину 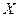 називають областю визначення відображення
називають областю визначення відображення 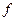 .
.
Множину 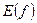 всіх елементів
всіх елементів 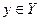 , кожний із яких має свій прообраз у множині
, кожний із яких має свій прообраз у множині 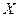 , називають областю значень відображення
, називають областю значень відображення 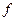 . Якщо
. Якщо 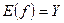 , тобто коли кожний елемент
, тобто коли кожний елемент 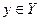 має свій прообраз, то говорять, що множина
має свій прообраз, то говорять, що множина 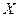 відображається на множину
відображається на множину 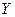 . Такі відображення називають сюр’єктивними.
. Такі відображення називають сюр’єктивними.
Якщо двом різним елементам 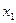 та
та 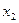 із множини
із множини 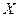 відповідають різні елементи множини
відповідають різні елементи множини 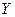 , тобто з того, що
, тобто з того, що 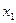
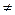
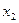 , випливає, що
, випливає, що 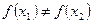 , то такі відображення називають ін’єктивними.
, то такі відображення називають ін’єктивними.
Відображення, які є одночасно ін’єктивними та сюр’єктивними, називають бієктивними або взаємно однозначними.
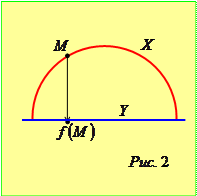
На рисунку 1 у ролі множини 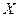 вибрано точки кола, а у ролі множини
вибрано точки кола, а у ролі множини 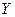 - точки діаметра цього кола. Відображення
- точки діаметра цього кола. Відображення 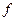 побудовано так, що кожній точці кола поставлено у відповідність її ортогональну проекцію на діаметр. Дане відображення є сюр’єктивним, але не ін’єктивним.
побудовано так, що кожній точці кола поставлено у відповідність її ортогональну проекцію на діаметр. Дане відображення є сюр’єктивним, але не ін’єктивним.
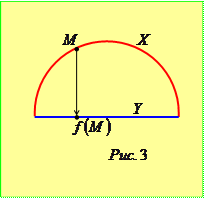
На рисунку 2 множину 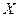 утворюють точки півкола, а множину
утворюють точки півкола, а множину 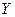 - точки прямої, яка містить діаметр кола. Відображення побудовано так, як і у попередньому прикладі. У даному випадку ми маємо приклад ін’єктивного, але не сюр’єктивного відображення.
- точки прямої, яка містить діаметр кола. Відображення побудовано так, як і у попередньому прикладі. У даному випадку ми маємо приклад ін’єктивного, але не сюр’єктивного відображення.
 Приклад бієктивного відображення наведено на рисунку 3, де
Приклад бієктивного відображення наведено на рисунку 3, де 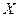 - точки півкола, а
- точки півкола, а 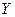 - точки його діаметра.
- точки його діаметра.
Якщо множини 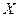 та
та 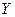 співпадають, то говорять про відображення множини
співпадають, то говорять про відображення множини 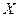 на себе. Нехай
на себе. Нехай 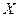 - множина точок площини (або деякої фігури
- множина точок площини (або деякої фігури 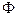 ), а
), а 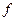 - взаємно однозначне відображення цієї множини на себе. У цьому випадку
- взаємно однозначне відображення цієї множини на себе. У цьому випадку 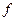 називають перетворенням площини (фігури
називають перетворенням площини (фігури 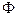 ).
).
Наведемо приклади окремих перетворень площини.
1. Нехай заданий вектор 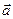 , паралельний до деякої площини. Довільній точці
, паралельний до деякої площини. Довільній точці  площини поставимо у відповідність точку
площини поставимо у відповідність точку  таку, що
таку, що 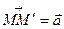 . Одержане перетворення, яке ми дальше будемо позначати символом
. Одержане перетворення, яке ми дальше будемо позначати символом 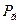 , називається паралельним перенесенням на вектор
, називається паралельним перенесенням на вектор 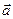 .
.
2. Нехай на площині задана деяка пряма 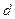 . Кожній точці
. Кожній точці  площини поставимо у відповідність симетричну їй відносно прямої
площини поставимо у відповідність симетричну їй відносно прямої 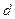 точку
точку  . Нагадаємо, що дві точки називаються симетричними відносно деякої прямої, якщо відрізок, який їх сполучає, перпендикулярний до даної прямої та ділиться нею пополам. Симетричними до точок на прямій вважаються ці самі точки. Побудоване таким чином відображення є перетворенням площини. Його називають симетрією відносно прямої або осьовою симетрією. Пряму
. Нагадаємо, що дві точки називаються симетричними відносно деякої прямої, якщо відрізок, який їх сполучає, перпендикулярний до даної прямої та ділиться нею пополам. Симетричними до точок на прямій вважаються ці самі точки. Побудоване таким чином відображення є перетворенням площини. Його називають симетрією відносно прямої або осьовою симетрією. Пряму 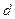 при цьому називають віссю симетрії. Розглянуте перетворення дальше будемо позначати символом
при цьому називають віссю симетрії. Розглянуте перетворення дальше будемо позначати символом 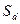 .
.
3. Зафіксуємо на площині деяку точку 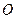 та поставимо у відповідність довільній точці
та поставимо у відповідність довільній точці  точку
точку  , симетричну їй відносно точки
, симетричну їй відносно точки 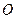 (тобто точка
(тобто точка 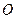 є серединою відрізка
є серединою відрізка 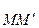 ). Симетричною до точки
). Симетричною до точки 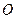 вважається ця сама точка. Побудоване перетворення площини називають симетрією відносно точки або центральною симетрією. Точку
вважається ця сама точка. Побудоване перетворення площини називають симетрією відносно точки або центральною симетрією. Точку 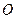 називають центром симетрії. Позначати перетворення центральної симетрії будемо символом
називають центром симетрії. Позначати перетворення центральної симетрії будемо символом 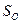 .
.
4. Розглянемо на площині деяку точку 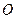 та орієнтований кут
та орієнтований кут 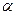 , тобто кут із вказаним на ньому напрямком повороту однієї сторони кута до суміщення з другою найкоротшим шляхом. Поставимо у відповідність довільній точці
, тобто кут із вказаним на ньому напрямком повороту однієї сторони кута до суміщення з другою найкоротшим шляхом. Поставимо у відповідність довільній точці  точку
точку  таку, що
таку, що 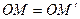 та орієнтовані кути
та орієнтовані кути 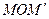 та
та 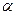 рівні. У цьому випадку кажуть, що точку
рівні. У цьому випадку кажуть, що точку  одержали в результаті повороту точки
одержали в результаті повороту точки  навколо точки
навколо точки 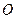 на кут
на кут 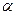 . Точці
. Точці 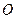 при цьому поставимо у відповідність цю саму точку. Ми одержали перетворення площини, яке називають поворотом навколо точки
при цьому поставимо у відповідність цю саму точку. Ми одержали перетворення площини, яке називають поворотом навколо точки 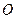 на кут
на кут 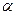 та позначають
та позначають 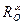 . Очевидно, що поворот навколо точки на кут
. Очевидно, що поворот навколо точки на кут 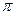 є центральною симетрією з центром у даній точці, тобто
є центральною симетрією з центром у даній точці, тобто 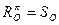 .
.
5. Поставимо у відповідність кожній точці площини цю саму точку. Дане перетворення площини називається тотожнім. Тотожне перетворення будемо позначати символом  .
.
Наведені приклади не вичерпують усі можливі види геометричних перетворень. Дальше ми детальніше розглянемо як дані, так і інші геометричні перетворення площини, а також їхні застосування.
Дата публикования: 2015-09-17; Прочитано: 2597 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
