 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Композиції деяких геометричних перетворень
|
|
Зупинимось на питанні композиції деяких геометричних перетворень.
Приклад 1. Нехай на площині задані дві точки 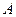 та
та 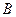 . Розглянемо перетворення площини, яке полягає у тому, що довільна точка
. Розглянемо перетворення площини, яке полягає у тому, що довільна точка  спочатку симетризується відносно точки
спочатку симетризується відносно точки 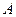 , а потім її образ симетризується відносно точки
, а потім її образ симетризується відносно точки 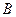 . Очевидно, що мова іде про композицію двох центральних симетрій
. Очевидно, що мова іде про композицію двох центральних симетрій 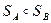 . Нехай
. Нехай 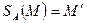 та
та 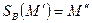 (рис. 5).
(рис. 5).
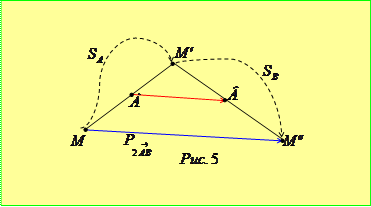
Якщо точка  не належить прямій
не належить прямій 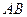 , то у трикутнику
, то у трикутнику 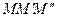 відрізок
відрізок 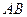 буде середньою лінією, тому
буде середньою лінією, тому 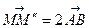 . Аналогічну рівність легко отримати і у випадку, коли точка
. Аналогічну рівність легко отримати і у випадку, коли точка  належить прямій
належить прямій 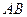 . Таким чином, композиція двох центральних симетрій переводить точку
. Таким чином, композиція двох центральних симетрій переводить точку  у точку
у точку 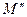 , тому має місце рівність
, тому має місце рівність
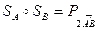 .
.
 Приклад 2. Нехай на площині задані три точки
Приклад 2. Нехай на площині задані три точки 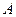 ,
, 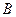 та
та 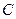 , які не лежать на одній прямій. Розглянемо питання, яке перетворення являє собою композиція трьох центральних симетрій відносно даних точок, тобто перетворення
, які не лежать на одній прямій. Розглянемо питання, яке перетворення являє собою композиція трьох центральних симетрій відносно даних точок, тобто перетворення 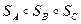 . Нехай
. Нехай 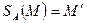 ,
, 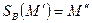 та
та 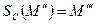 , а також точка
, а також точка 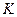 є серединою відрізка
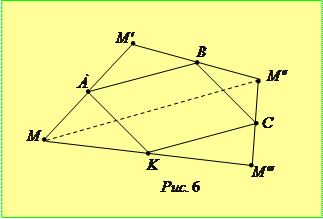
є серединою відрізка 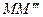 (рис. 6). Тоді чотирикутник
(рис. 6). Тоді чотирикутник 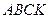 буде паралелограмом, оскільки відрізки
буде паралелограмом, оскільки відрізки 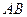 та
та  рівні та паралельні (вони є середніми лініями трикутників
рівні та паралельні (вони є середніми лініями трикутників 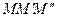 та
та 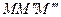 ). Таким чином, точки
). Таким чином, точки  та
та 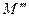 симетричні відносно точки
симетричні відносно точки 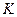 .
.
Отже,
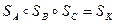 ,
,
де точка 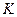 - четверта вершина паралелограма
- четверта вершина паралелограма 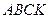 .
.
Застосуємо одержаний факт до розв’язання задачі про побудову п’ятикутника за серединами його сторін.
 Нехай
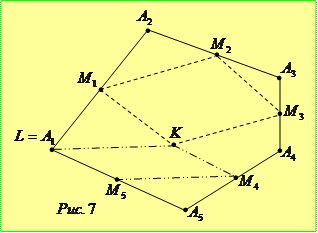
Нехай 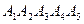 - шуканий п’ятикутник та точки
- шуканий п’ятикутник та точки 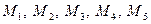 - середини його сторін (рис. 7). Очевидно, що для розв’язання задачі достатньо знайти хоча б одну вершину п’ятикутника.
- середини його сторін (рис. 7). Очевидно, що для розв’язання задачі достатньо знайти хоча б одну вершину п’ятикутника.
Проведемо аналіз. При симетрії вершини 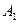 відносно точки
відносно точки 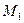 одержимо точку
одержимо точку 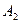 . Симетрія її відносно точки
. Симетрія її відносно точки 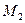 дає точку
дає точку 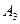 . Продовжуючи аналогічні міркування дальше, в кінці ми симетризуємо вершину
. Продовжуючи аналогічні міркування дальше, в кінці ми симетризуємо вершину 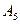 відносно точки
відносно точки 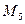 та одержимо початкову точку
та одержимо початкову точку 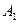 .
.
Таким чином отримуємо рівність
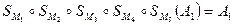 . (2)
. (2)
Використовуючи результати прикладу 3, дістаємо, що
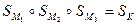 ,
,
де 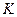 - четверта вершина паралелограма
- четверта вершина паралелограма 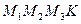 . Тому рівняння (2), у якому невідомим є точка
. Тому рівняння (2), у якому невідомим є точка 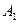 , можна спростити до виду
, можна спростити до виду
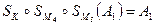 .
.
Оскільки 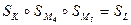 , де
, де 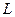 - четверта вершина паралелограма
- четверта вершина паралелограма 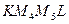 , то отримуємо рівність
, то отримуємо рівність 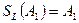 , яка можлива тільки тоді, коли точки
, яка можлива тільки тоді, коли точки 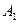 та
та 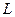 співпадають.
співпадають.
Таким чином, для відшукання невідомої вершини п’ятикутника спочатку, використавши точки 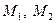 та
та 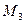 , знаходять точку
, знаходять точку 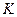 - четверту вершину паралелограма
- четверту вершину паралелограма 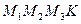 , а потім будують шукану точку
, а потім будують шукану точку 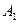 , як четверту вершину паралелограма
, як четверту вершину паралелограма 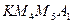 .
.
Приклад 3. Розглянемо композицію двох осьових симетрій відносно паралельних прямих 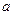 та
та  , тобто перетворення
, тобто перетворення 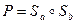 . Нехай відстань між прямими дорівнює
. Нехай відстань між прямими дорівнює 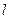 . Щоб встановити вид перетворення
. Щоб встановити вид перетворення  введемо у розгляд прямокутну декартову систему координат, направивши вісь
введемо у розгляд прямокутну декартову систему координат, направивши вісь  по прямій
по прямій 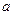 . Нехай пряма
. Нехай пряма  перетинає вісь
перетинає вісь 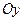 у точці
у точці 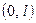 . Тоді при осьовій симетрії відносно прямої
. Тоді при осьовій симетрії відносно прямої 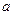 точка
точка 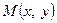 перейде у точку
перейде у точку 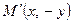 , а при осьовій симетрії відносно прямої
, а при осьовій симетрії відносно прямої  точка
точка  перейде у точку
перейде у точку 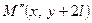 , оскільки точка
, оскільки точка 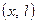 є серединою відрізка
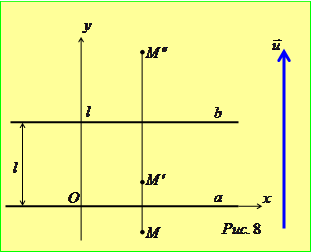
є серединою відрізка 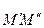 (рис. 8). Звернувши увагу на те, що вектор
(рис. 8). Звернувши увагу на те, що вектор 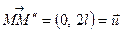 не залежить від вибору точки
не залежить від вибору точки  , робимо висновок, що перетворення
, робимо висновок, що перетворення  є паралельне перенесення на вектор
є паралельне перенесення на вектор 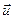 , довжина якого дорівнює подвійній відстані між прямими
, довжина якого дорівнює подвійній відстані між прямими 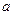 та
та  і який напрямлений перпендикулярно до заданих прямих від прямої
і який напрямлений перпендикулярно до заданих прямих від прямої 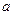 до прямої
до прямої  . Таким чином,
. Таким чином,
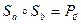 .
.
Одержану рівність можна розуміти і навпаки, а саме: довільне паралельне перенесення на вектор 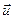 можна замінити композицією двох осьових симетрій відносно двох паралельних прямих, проведених перпендикулярно до вектора
можна замінити композицією двох осьових симетрій відносно двох паралельних прямих, проведених перпендикулярно до вектора 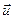 та розташованих на відстані
та розташованих на відстані 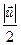 .
.
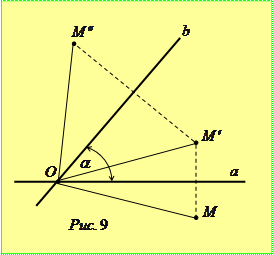
Приклад 4. Розглянемо композицію двох осьових симетрій відносно двох прямих 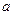 та
та  , які перетинаються. Позначимо дане перетворення
, які перетинаються. Позначимо дане перетворення 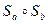 через
через 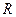 та встановимо його вид. Будемо вважати, що дані прямі перетинаються у деякій точці
та встановимо його вид. Будемо вважати, що дані прямі перетинаються у деякій точці 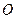 та утворюють кут
та утворюють кут 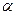 . Нехай при осьовій симетрії відносно прямої
. Нехай при осьовій симетрії відносно прямої 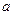 точка
точка  перейде у точку
перейде у точку  , а при осьовій симетрії відносно прямої
, а при осьовій симетрії відносно прямої  точка
точка  перейде у точку
перейде у точку 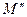 (рис. 9). Легко бачити, що
(рис. 9). Легко бачити, що 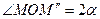 , а також, що
, а також, що 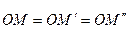 . Тому перетворення
. Тому перетворення 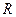 є поворот навколо точки
є поворот навколо точки 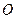 на кут
на кут 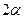 :
: 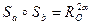 .
.
 Навпаки, будь-який поворот навколо точки
Навпаки, будь-який поворот навколо точки 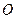 на кут
на кут 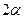 можна розглядати, як композицію двох осьових симетрій відносно двох прямих, які перетинаються у точці
можна розглядати, як композицію двох осьових симетрій відносно двох прямих, які перетинаються у точці 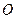 та утворюють кут
та утворюють кут 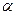 .
.
Дата публикования: 2015-09-17; Прочитано: 1367 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
