Застосування інваріантів для побудови ліній другого порядку

Розглянемо питання побудови ліній другого порядку за допомогою інваріантів.

Використовуючи коефіцієнти рівняння (1), обчислимо інваріанти 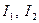та 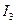. Нехай 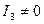. Тоді, знайшовши корені характеристичного рівняння 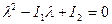, рівняння лінії можна записати у виді (12) або (14). Для побудови лінії за одержаним рівнянням потрібно зобразити нову систему координат. Для цього шукають центр лінії при 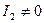або шукають вершину параболи у випадку, коли 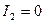- це координати нового початку. Потім виконують поворот системи координат на кут .

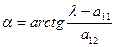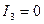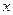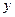У випадку, коли , як ми мали можливість переконатися, лінія другого порядку вироджується у дві прямі, а її рівняння можна представити у вигляді рівності нулю добутку двох лінійних множників. Щоб знайти дані множники рівняння (1) розв’язують, як квадратне відносно змінної або . Одержавши рівняння прямих, їх будують у початковій системі координат. Проілюструємо сказане вище на окремих прикладах.

Приклад 1. Звести до канонічного виду рівняння лінії 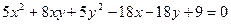та побудувати її.

Розв’язання. Виконаємо наступні обчислення:

, , .

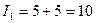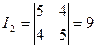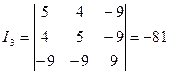Характеристичне рівняння запишеться у виді 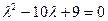та має корені 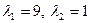. Використавши рівняння (12), запишемо початкове рівняння у виді 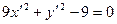, або

.

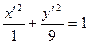Одержали канонічне рівняння еліпса. Для зображення системи координат, в якій еліпс задається даним канонічним рівнянням, знайдемо його центр. Із системи

дістаємо 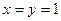. Знайдено початок нової системи координат – точку 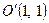. Для відшукання кута повороту дістаємо

.

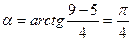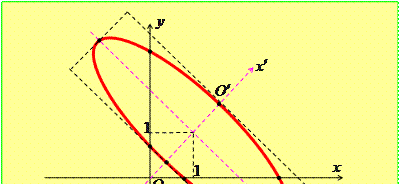
Залишається зобразити нову систему координат та побудувати в ній еліпс за його канонічним рівняння (рис. 1). Пропонуємо порівняти одержаний результат із міркуваннями, наведеними у лекціях 19 – 20 (задача 7), де дана лінія була зображена, як підсумок дослідження її властивостей.

Приклад 2. Звести до канонічного виду рівняння лінії 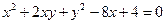та побудувати її.

Розв’язання. Виконаємо аналогічні до попереднього прикладу обчислення:

, , .

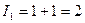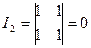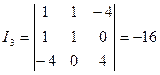Характеристичне рівняння 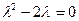має корені 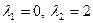. Рівняння параболи, відповідно до рівності (14), запишемо у виді 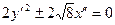або 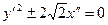. Для відшукання нової системи координат спочатку знайдемо вершину параболи. Для цього розв’яжемо систему рівнянь

.

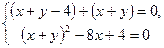Отримуємо 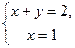, звідки знаходимо 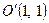. Поворот системи координат здійснюється на кут .

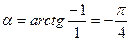Зауважимо, що даний приклад ми уже розглядали у попередній лекції (задача 4), але розв’язували його іншим методом. Там же наведено зображення даної лінії (рис. 4).

Приклад 3. Встановити вид лінії, заданої рівнянням .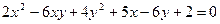

Розв’язання. Обчислимо інваріант .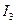

.

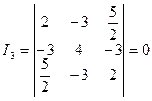Оскільки 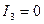, то рівняння задає вироджену лінію. Тому розв’яжемо його, як квадратне відносно однієї із змінних, нехай змінної 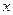. Дістаємо

,

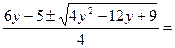
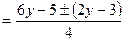звідки 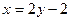та 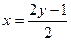. За допомогою знайдених коренів задане рівняння можна записати у виді 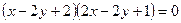. Очевидно, що воно задає дві прямі 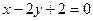та .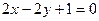

Відповідь. Дві прямі 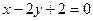та 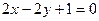, що перетинаються.