 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Рівняння конічних перерізів
|
|
Розглянуті нами лінії другого порядку – еліпс, гіперболу та параболу називають також конічними перерізами. Основою для такої назви є те, що дані лінії можна одержати, перетинаючи круговий конус площинами, які не проходять через вершину конуса. Зокрема площини, які проходять паралельно до осі конуса, перетинають його по гіперболах, а площини, які проходять паралельно до довільної твірної, перетинають конус по параболах. Площини, які не паралельні ні до осі конуса, ні до його твірних, перетинають конус по еліпсах (рис. 11) (у випадку перпендикулярності площини до осі конуса в перетині утворюється коло). Ми не будемо зупинятися на дещо громіздких доведеннях цих фактів. Їх можна знайти, наприклад, в  . Відмітимо тільки, що наведені твердження були відомі ще древньогрецькому математику Аполлонію Пергському, який займався дослідженням подібних питань у другому столітті до нашої ери.
. Відмітимо тільки, що наведені твердження були відомі ще древньогрецькому математику Аполлонію Пергському, який займався дослідженням подібних питань у другому столітті до нашої ери.

Пригадаємо директоріальні властивості еліпса та гіперболи. Вони говорять про те, що для кожної точки цих ліній відношення відстаней від неї до фокуса та відповідної директриси є стала величина, яка дорівнює ексцентриситету лінії. Оскільки кожна точка параболи рівновіддалена від фокуса та директриси, то і у цьому випадку відношення даних відстаней є сталим числом, яке дорівнює 1 (це число ми назвали ексцентриситетом параболи). Ця спільна властивість ліній лежить в основі виведення рівнянь конічних перерізів у полярних координатах.
 Нехай точка
Нехай точка 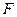 є фокусом, а пряма
є фокусом, а пряма 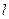 - відповідною директрисою лінії другого порядку з ексцентриситетом
- відповідною директрисою лінії другого порядку з ексцентриситетом 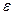 . Побудуємо полярну систему координат, вибравши фокус
. Побудуємо полярну систему координат, вибравши фокус 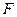 полюсом та спрямувавши полярну вісь по прямій, яка перпендикулярна до директриси, але так, щоб вона не перетинала пряму
полюсом та спрямувавши полярну вісь по прямій, яка перпендикулярна до директриси, але так, щоб вона не перетинала пряму 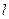 (рис. 12). Будемо вважати, що відстань від точки
(рис. 12). Будемо вважати, що відстань від точки 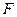 до прямої
до прямої 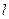 дорівнює
дорівнює 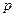 .
.
Нехай 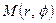 – довільна точка лінії. Обчислимо відстань
– довільна точка лінії. Обчислимо відстань 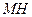 від неї до прямої
від неї до прямої 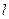 . Для цього з точки
. Для цього з точки 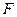 опустимо перпендикуляр
опустимо перпендикуляр 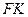 на пряму
на пряму 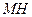 . Оскільки
. Оскільки 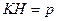 та
та 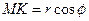 , то
, то 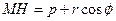 . Використовуючи директоріальну властивість, можемо записати, що
. Використовуючи директоріальну властивість, можемо записати, що 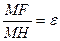 , або
, або
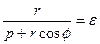 . (3)
. (3)
Розв’язуючи рівняння (3) відносно 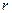 , дістаємо
, дістаємо
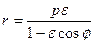 . (4)
. (4)
Одержане співвідношення називають рівнянням конічних перерізів у полярнихкоординатах. При 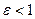 воно визначає еліпс, при
воно визначає еліпс, при 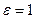 – параболу, а при
– параболу, а при 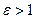 – гіперболу.
– гіперболу.
Зробимо наступні зауваження.
У випадку еліпса знаменник 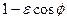 не перетворюється в нуль для жодного значення
не перетворюється в нуль для жодного значення 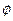 . Це означає, що всі точки лінії розташовані від фокуса на відстані, що не перевищує певного числа. Очевидно, що це характерно тільки для еліпса.
. Це означає, що всі точки лінії розташовані від фокуса на відстані, що не перевищує певного числа. Очевидно, що це характерно тільки для еліпса.
Для параболи знаменник 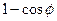 перетвориться в нуль тільки при
перетвориться в нуль тільки при 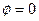 . Тому існує єдиний напрям, при прямуванні до якого точки лінії нескінченно віддаляються.
. Тому існує єдиний напрям, при прямуванні до якого точки лінії нескінченно віддаляються.
У випадку гіперболи рівняння 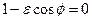 на проміжку (
на проміжку (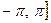 має два розв’язки
має два розв’язки 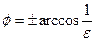 . Це означає, що існує два напрямки, при наближенні до яких точки лінії нескінченно віддаляються. Очевидно, що асимптоти гіперболи паралельні до прямих
. Це означає, що існує два напрямки, при наближенні до яких точки лінії нескінченно віддаляються. Очевидно, що асимптоти гіперболи паралельні до прямих 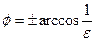 . При цьому точки лінії, для яких виконується нерівність
. При цьому точки лінії, для яких виконується нерівність 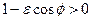 , тобто, коли
, тобто, коли 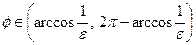 , належать одній із віток гіперболи. Значення
, належать одній із віток гіперболи. Значення 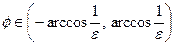 , для яких виконується нерівність
, для яких виконується нерівність 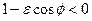 , дозволяють отримати точки другої вітки гіперболи. Для побудови цієї вітки потрібно використовувати узагальнені полярні координати.
, дозволяють отримати точки другої вітки гіперболи. Для побудови цієї вітки потрібно використовувати узагальнені полярні координати.
Наведемо приклади задач.
Задача 1. Встановити, яку лінію задає рівняння 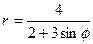 . У випадку лінії другого порядку визначити її ексцентриситет та відстань від фокуса до відповідної директриси.
. У випадку лінії другого порядку визначити її ексцентриситет та відстань від фокуса до відповідної директриси.
Розв’язання. Виконаємо наступні перетворення:
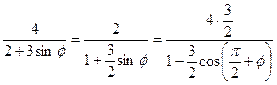 .
.
Тепер очевидно, що рівняння  , де
, де 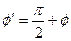 , визначає гіперболу з ексцентриситетом
, визначає гіперболу з ексцентриситетом  , для якої відстань
, для якої відстань 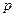 від фокуса до відповідної директриси дорівнює 4. Той факт, що задане рівняння визначає гіперболу можна було встановити без перетворень виразу, оскільки його знаменник
від фокуса до відповідної директриси дорівнює 4. Той факт, що задане рівняння визначає гіперболу можна було встановити без перетворень виразу, оскільки його знаменник 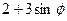 на проміжку (
на проміжку (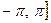 перетворюється в нуль у двох точках. Заміна
перетворюється в нуль у двох точках. Заміна 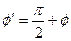 , виконана нами в процесі перетворень, означає перехід до нової полярної системи координат із тим же полюсом та новою полярною віссю, яку можна одержати поворотом попередньої осі навколо полюса на кут
, виконана нами в процесі перетворень, означає перехід до нової полярної системи координат із тим же полюсом та новою полярною віссю, яку можна одержати поворотом попередньої осі навколо полюса на кут 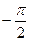 .
.
Задача 2. Знайти канонічне рівняння гіперболи 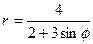 .
.
Розв’язання. Використовуючи рівності (2), дістаємо
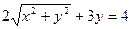 ,
,
звідки, позбувшись ірраціональності, отримуємо рівняння
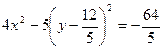 .
.
Вводячи заміну 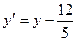 , дістаємо шукане рівняння у виді
, дістаємо шукане рівняння у виді 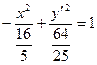 .
.
Відповідь: 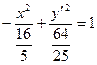 .
.
Дата публикования: 2015-09-17; Прочитано: 1061 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
