 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные характеристики экспоненциального распределения случайной величины
|
|
Математическое ожидание или средняя наработка до отказа:
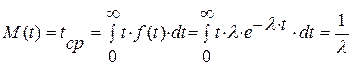 .
.
Дисперсия:
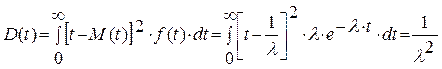 .
.
Среднеквадратическое отклонение:
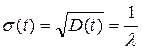 .
.
Коэффициент вариации:
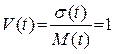 .
.
Практически экспоненциальный закон распределения вероятностей случайной величины применяется при рассмотрении наработки невосстанавливаемого изделия до его случайного отказа. Это, например, некоторые типы электрических ламп, некоторые электрические датчики, а также элементы изделий химического машиностроения. У восстанавливаемых изделий случайными являются промежутки времени между последовательными отказами, которые при установившемся режиме работы технического объекта часто подчиняются экспоненциальному закону распределения.
Распределение Вейбулла – это распределение непрерывной случайной величины, которая может принимать только положительные значения с плотностью распределения вероятностей
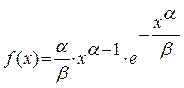 .
.
Функция распределения:
 .
.
Вероятность безотказной работы:
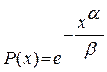 ,
,
где 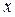 – величина переменная;
– величина переменная; 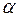 и
и 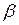 – постоянные параметры:
– постоянные параметры: 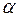 – параметр формы;
– параметр формы; 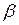 – параметр масштаба.
– параметр масштаба.
Распределение Вейбулла применяется при расчетах долговечности технических объектов, для описания сроков службы различных элементов машин. Оно хорошо описывает отказы механических систем в начальный период эксплуатации и отказы из-за хрупких и усталостных разрушений. У шарикоподшипников наработка до отказа подчиняется этому распределению с показателем 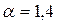 , у электронных ламп
, у электронных ламп  .
.
При 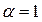 получим экспоненциальное распределение. Для определения параметров
получим экспоненциальное распределение. Для определения параметров 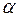 и
и 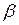 существуют специальные формулы.
существуют специальные формулы.
Графики 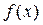 и
и  распределения Вейбулла при различных значениях параметра
распределения Вейбулла при различных значениях параметра 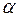 приведены на рис. 2.
приведены на рис. 2.
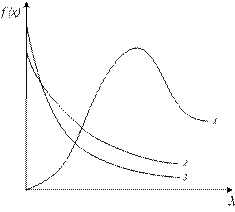
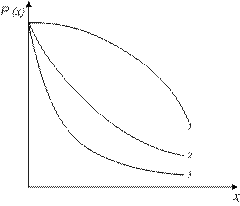
а) б)
Рис. 2. Графики: а) плотности распределения вероятностей 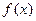 и
и
б) вероятности безотказной работы 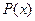 при значениях параметра
при значениях параметра  :
:
1 – 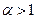 ; 2 –
; 2 – 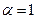 ; 3 –
; 3 – 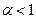
Нормальное распределение – распределение непрерывной случайной величины, которая может принимать как отрицательные, так и положительные значения во всем диапазоне возможных значений от 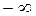 до
до 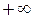 .
.
В этом отличие нормального распределения от ранее рассмотренных законов.
Плотность распределения вероятностей имеет вид:
 ,
,
где 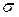 – положительная величина;
– положительная величина; 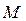 – любая положительная, отрицательная величина или нуль.
– любая положительная, отрицательная величина или нуль.
Графики 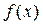 и
и 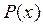 нормального распределения приведены на рис. 3.
нормального распределения приведены на рис. 3.
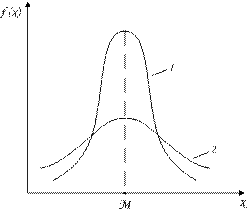
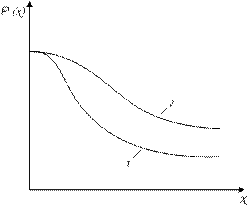
а) б)
Рис.3. Графики: а) плотности распределения вероятностей 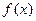 и
и
б) вероятности безотказной работы 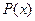 при значениях параметров:
при значениях параметров:
1 – 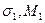 ; 2 –
; 2 – 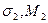 (
( ,
,  )
)
Значит, математическое ожидание 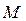 – это среднее значение случайной величины, а
– это среднее значение случайной величины, а 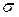 – среднеквадратическое отклонение, определяющее величину рассеивания вокруг центра распределения.
– среднеквадратическое отклонение, определяющее величину рассеивания вокруг центра распределения.
Коэффициент вариации  изменяется от
изменяется от 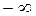 до
до 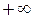 .
.
Рассмотрим частный случай: 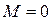 ,
, 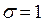 , тогда:
, тогда:
 .
.
Это нормированное и центрированное распределение одной переменной легко табулируется и для него есть подробные таблицы.
Возьмем несколько значений случайной величины 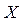 и соответствующие им значения
и соответствующие им значения 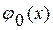 с четырьмя знаками после запятой (табл. 1).
с четырьмя знаками после запятой (табл. 1).
Таблица 1
Значения функции 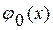

| |||||
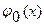
| 0,3989 | 0,2420 | 0,0540 | 0,0044 | 0,0001 |
Среднее значение случайной величины – 0, среднеквадратическое отклонение – 1.
Если мы отойдем от 0 на 3 среднеквадратических отклонения, то 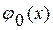 получается очень малым. Поэтому на практике говорят, что если от центра нормального распределения отложить
получается очень малым. Поэтому на практике говорят, что если от центра нормального распределения отложить 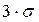 вправо, то практически дальше уже распределение отсутствует.
вправо, то практически дальше уже распределение отсутствует.
В силу симметрии то же самое будет, если отложить 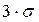 влево. Для более точной картины нужно отложить
влево. Для более точной картины нужно отложить  .
.
Это так называемое правило 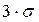 : если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения.
: если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения.
При помощи таблицы значений функции 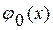 легко можно вычислить плотность вероятности нормального распределения и тогда, когда
легко можно вычислить плотность вероятности нормального распределения и тогда, когда  и
и  .
.
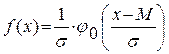 .
.
Рассмотрим функцию распределения:
 .
.
В частном случае при 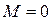 и
и 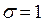 получаем
получаем
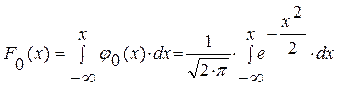 .
.
Для этой функции также есть таблица, с помощью которой легко вычислить функцию распределения для общего случая по следующей формуле:
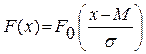 .
.
Для тех же значений случайной величины 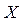 приведем в табл. 2 значения нормированной и центрированной функции распределения
приведем в табл. 2 значения нормированной и центрированной функции распределения 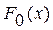 .
.
Таблица 2
Значения функции 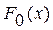

| |||||
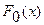
| 0,5 | 0,8413 | 0,9772 | 0,9986 | 1,0000 |
Отсюда видно, что если ограничиться интервалом, равным 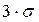 , то почти полностью охватывается все распределение.
, то почти полностью охватывается все распределение.
Вероятность отсутствия отказа:
 .
.
Понятие квантили. В табл. 2 даны «круглые» значения случайной величины 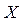 и соответствующие им значения функции распределения вероятностей
и соответствующие им значения функции распределения вероятностей 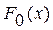 . Можно задаваться «круглыми» значениями функции распределения вероятностей
. Можно задаваться «круглыми» значениями функции распределения вероятностей 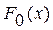 и искать значения случайной величины
и искать значения случайной величины 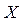 . Значения случайной величины
. Значения случайной величины 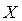 , соответствующие «круглому» значению функции распределения
, соответствующие «круглому» значению функции распределения 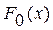 , называются квантилью.
, называются квантилью.
Если для «круглого» значения 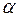 функции распределения вероятностей
функции распределения вероятностей 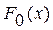 обозначить квантиль через
обозначить квантиль через 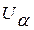 , то получим уравнение
, то получим уравнение
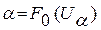 .
.
В табл. 3 приведено несколько значений квантилей.
Таблица 3
Квантили
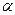
| 0,9 | 0,95 | 0,99 | 0,999 | 0,9999 |

| 1,282 | 1,645 | 2,326 | 3,090 | 3,719 |
Нормальный закон распределения вероятностей случайной величины хорошо описывает наработку объекта до отказа, являющегося следствием износа и старения, а также ошибки, возникающие при различного рода измерениях.
Логарифмически нормальное распределение имеет случайная величина  , если ее логарифм
, если ее логарифм 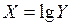 распределен нормально, т.е. плотность распределения вероятностей имеет вид:
распределен нормально, т.е. плотность распределения вероятностей имеет вид:
 ,
,
где  .
.
На рис. 4 приведены графики 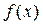 логарифмически нормального распределения случайной величины.
логарифмически нормального распределения случайной величины.
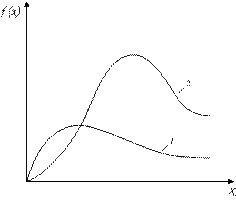
Рис.4. Графики плотности распределения вероятностей 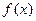 :
:
1 – для 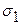 , 2 – для
, 2 – для  (
(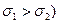
Логарифмически нормальный закон распределения вероятностей применяется для описания следующих случайных величин:
- наработки объекта до отказа, вызванного усталостными разрушениями;
- ремонтопригодности, когда случайное время простоя вызвано затратами времени на отыскание и устранение причины отказа.
Композиция законов распределения. Пусть имеется несколько случайных величин, например, три: случайная величина 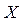 , у которой плотность распределения вероятностей
, у которой плотность распределения вероятностей 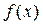 ; случайная величина
; случайная величина  , у которой плотность распределения вероятностей
, у которой плотность распределения вероятностей 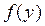 ; случайная величина
; случайная величина 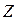 , у которой плотность распределения вероятностей
, у которой плотность распределения вероятностей 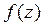 .
.
Рассмотрим величину  .
.
Если  – случайные величины, их сумма тоже будет случайной величиной. Если
– случайные величины, их сумма тоже будет случайной величиной. Если 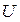 – случайная величина, то она имеет плотность распределения вероятностей
– случайная величина, то она имеет плотность распределения вероятностей 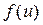 .
.
Закон распределения случайной величины, которая является суммой нескольких случайных величин, называется композицией законов распределения этих величин.
Из трех законов – 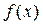 ,
, 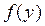 и
и 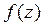 – получен новый закон
– получен новый закон 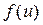 .
.
Композиция законов имеет ряд общих и частных свойств.
Общими называются такие свойства, которые не зависят от вида рассматриваемых законов распределения, а частными – такие, которые применимы к конкретным законам распределения.
Общие свойства:
1. Математическое ожидание:
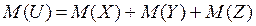 .
.
У композиции математическое ожидание находится как сумма математических ожиданий трех данных законов. Это справедливо для любого количества законов распределения.
2. Дисперсия:
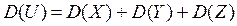 или
или 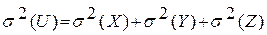 .
.
Пример: пусть имеется композиция двух законов 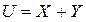 с характеристиками
с характеристиками 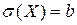 и
и 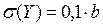 .
.
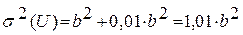 ;
;
 .
.
Для величины 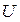 мы получили среднеквадратическое отклонение, приблизительно равное
мы получили среднеквадратическое отклонение, приблизительно равное 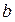 . Таким образом, если имеем две случайные величины, у которых резко отличаются друг от друга среднеквадратические отклонения, то в результате композиции влияние той случайной величины, которая имеет меньшую дисперсию, аннулируется.
. Таким образом, если имеем две случайные величины, у которых резко отличаются друг от друга среднеквадратические отклонения, то в результате композиции влияние той случайной величины, которая имеет меньшую дисперсию, аннулируется.
Частные свойства:
1. Композиция любого количества нормальных распределений дает снова нормальное распределение.
Рассмотрим два экспоненциальных распределения. Пусть случайные величины 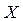 и
и  имеют одинаковое экспоненциальное распределение с параметром
имеют одинаковое экспоненциальное распределение с параметром 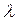 .
.
Тогда имеем:
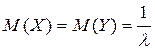 ;
;
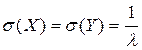 ;
;
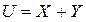 ;
;
M(U)= 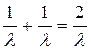 ;
;
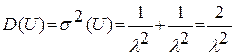 ;
;
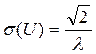 ;
;
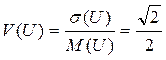 .
.
В композиции мы получили не экспоненциальное распределение, так как 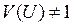 .
.
Из всех распределений только два обладают указанным выше свойством (в композиции давать такое же распределение) – нормальное и Пуассона.
2. Если взять большое количество распределений (обычно больше 9) какой угодно природы, то их композиция будет близкой к нормальному распределению. Даже если взять большое количество неодинаковых распределений, с разной дисперсией, разными математическими ожиданиями и разной природы, то в итоге получим нормальное распределение.
Это важное положение теории вероятностей называется центральной предельной теоремой, которая определяет особую роль нормального распределения в теории вероятности и в теории надежности.
3. Пусть случайная величина 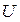 равна произведению логарифмически нормальных случайных величин
равна произведению логарифмически нормальных случайных величин  .
.
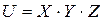 .
.
Прологарифмируем данное уравнение:
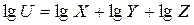 .
.
Если случайная величина равна произведению случайных величин, логарифмы которых распределены нормально, то данная случайная величина также имеет логарифмически нормальное распределение.
Суперпозиция распределений. Пусть имеется две партии изделий, изготовленных разными рабочими или из разных партий сырья в разные смены.
Пусть  – количество изделий в первой партии и размер изделия – случайная величина
– количество изделий в первой партии и размер изделия – случайная величина 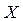 – имеет плотность распределения вероятностей
– имеет плотность распределения вероятностей 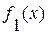 .
.
Пусть 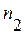 – количество изделий во второй партии и размер изделия – случайная величина
– количество изделий во второй партии и размер изделия – случайная величина 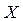 – имеет плотность распределения вероятностей
– имеет плотность распределения вероятностей 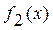 .
.
Образуем новую партию, смешав  изделий первой партии с
изделий первой партии с 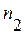 изделиями второй партии. Тогда получим новое распределение случайной величины
изделиями второй партии. Тогда получим новое распределение случайной величины 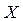 с плотностью распределения вероятностей
с плотностью распределения вероятностей 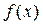 , которое называется суперпозицией распределений
, которое называется суперпозицией распределений 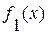 и
и 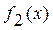 .
.
Суперпозицией распределений случайной величины 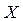 называется распределение, рассчитываемое по уравнению:
называется распределение, рассчитываемое по уравнению:
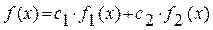 ,
,
где 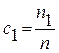 и
и 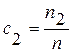 ;
;  и
и  .
.
С суперпозицией распределений часто встречаются, когда имеют дело с партией изделий, полученной при смешении изделий, изготовленных разными рабочими, в разные дни, в разные смены, из разных полуфабрикатов и т.п.
Если для 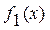 имеем
имеем 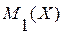 и
и 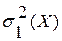 , а для
, а для 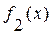 –
– 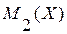 и
и 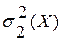 , то для суперпозиции распределений получаем следующие характеристики:
, то для суперпозиции распределений получаем следующие характеристики:
 ;
;
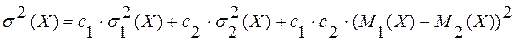 .
.
Дата публикования: 2015-09-17; Прочитано: 2096 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
