Для получения графической интерпретации используется следующий алгоритм

Комплексное число z=x+iy может быть изображено на плоскости точкой с координатами
(x, y). Изображение строится в некоторой прямоугольной области с разрешением n * m точек.

Формула итераций для фрактала Мандельброта выглядит следующим образом:

z_{k+ 1} = z_k ² + z ₀, k= 0, 1, 2, …

Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне для x ₀ = (от -2,2 до 1), для y ₀=(от -1,2 до 1,2) – начальные точки z ₀.

Для каждой начальной точки вычисляется количество k точек, попадающих в круг сходимости (k – число итераций). Условием завершения итераций является |z_k|> 2.

Суть алгоритма сводится к итерационному выводу точек, попадающих в круг сходимости для каждой начальной точки, в пределах заданного графического окна. Для каждого цикла итерации (для каждой начальной точки) выбирается свой цвет.

Если принять значения k для каждой начальной точки (x, y) в качестве высот некоторой поверхности в данной точке можно построить объемное изображение множества Мандельброта или его части, которое при специально подобранном освещении может выглядеть и как скала с плоской вершиной, и как водопад, и как горная пещера.

Типичный фрактал, каким является множество Мандельброта, представляет собой иерархический объект, состоящий из родительского тела в форме кардиоиды и многочисленных потомков, повторяющих форму предков, от которых они ответвляются. Само подобие элементов фрактала хорошо видно на его изображении.

Связность множества означает, что его элементы, даже самого малого размера, которые Мандельброт назвал "фрактальной пылью", не обособлены, а соединены тончайшими нитями в одно целое. Продолжая процесс увеличения пограничных областей, мы всюду видим бесконечное разнообразие форм, поражающих гармонией, великолепием и удивительным сходством с изображениями регулярно-хаотических явлений природы: молний, снежинок, ледяного узора, инея на ветвях деревьев, кораллов, паутины, солнечных протуберанцев, звездных скоплений и т.п.

В математике множество Мандельброта — это фрактал, определённый как множество точек c на комплексной плоскости, для которых итеративная последовательность
z₀ = 0
z_n+1 = z_n² + c
не уходит на бесконечность.

По сути мы имеем некоторые начальные условния (z₀= 0) и формулу, которая позволяет из шага N получить шаг N + 1. Шагов таких может быть стопятьсот. Потому по-хорошему их нужно ограничить. Если за некоторое количество шагов z далеко не ушло, будем считать, что и не уйдёт.

Из вышенаписанного можно сделать вывод, что фрактал правильно рисовать двумя цветами. Одним цветом точки, принадлежащие фракталу, другим — не пренадлежащие. Но получится не очень красиво. Потому часто фракталы разукрашивают. Самый простой способ — считать число шагов N и чем их больше, тем ярче рисовать текущий пиксель.

Фрактал Джулио (Жюлио) внешне совсем не похож на фрактал Мандельброта, хотя формула итераций для этого фрактала почти полностью совпадает с формулой для фрактала Мандельброта:

z_{k+ 1} = z_k ² + c, k= 0, 1, 2, …

где c – комплексная константа.

Если при генерации фрактала Мандельброта значение z ₀ каждый раз совпадает со значением в начальной точке на данном шаге итераций, то для фрактала Джулио значение c всегда одно и то же комплексное число.

В программе, (приведенной в приложении 2), построено изображение фрактала Джулио для c= 0,36+ i* 0,36.

Итерационная формула для фрактала Джулио имеет вид

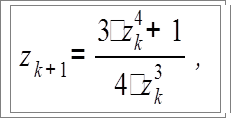
где z – также комплексные числа, причем z ₀ =x+iy соответствует координатам точки изображения. Условием прекращения цикла итераций для фрактала Ньютон есть приближение значений |z ⁴ - 1| к нулю.

Границы расчета: для x – от -1 до 1, для y – от -1 до 1.

Множество Мандельброта — это множество, таких точек c на комплексной плоскости, для которых итеративная последовательность z ₀=0, z_n = z_{n -1}²+ c (n =1, 2, 3, …) не уходит на бесконечность. То есть, это множество таких c, для которых существует действительное R, что неравенство | z_n |< R выполняется при всех натуральных n.

Множество Мандельброта является в некотором смысле фракталом. Его фрагменты не строго подобны исходному множеству, но при многократном увеличении определённые части всё больше похожи друг на друга.

Таким образом, вышеуказанная последовательность может быть раскрыта для каждой точки на комплексной плоскости следующим образом:

С = x + i * y

Z₀ = 0; Z₁ = Z₀² + c = x+ iy; Z₂ = Z₁² + c = (x+iy)² + x +iy = x²-y²+x+(2xy+y)I; и т.д.

Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём самая большая в центре представляет собой кардиоиду. Также есть набор овалов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих овалов имеет свой набор меньших овалов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой. Самая большая фигура (видимая при рассматривании основного множества) из них находится в области от −1,78 до −1,75 на отрицательной оси действительных значений.

Фрактал Джулио

В голоморфной динамике, множество Жюлиа J(f) рационального отображения — f: CP¹ -> CP¹ множество точек, динамика в окрестности которых в определённом смысле неустойчива по отношению к малым возмущениям начального положения. В случае, если f — полином, рассматривают также заполненное множество Жюлиа — множество точек, не стремящихся к бесконечности. Обычное множество Жюлиа при этом является его границей.

Свойства

· Как следует из определений, множество Жюлиа всегда замкнуто.

· Множество Жюлиа является замыканием объединения всех отталкивающих периодических орбит.

Множество Жюлиа инвариантно относительно динамики — оно оказывается имеющим фрактальную структуру: его маленькие части похожи на большие