Канонические уравнения поверхностей второго порядка

Основные определения

Эллипсоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

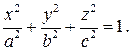
Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

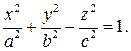
Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

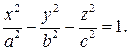
Эллиптическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

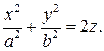
Гиперболическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

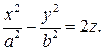
Эллиптическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

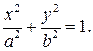
Гиперболическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

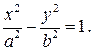
Параболическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение

у² = 2рх.

Основные утверждения

Утверждение 1. Общее уравнение поверхности второго порядка в общей декартовой системе координат

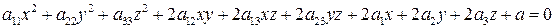
имеет в канонической прямоугольной системе координат один из 17 канонических видов. из которых 8 – перечисленные поверхности, остальные представляют собой плоскости (2 или 1), линии, точки или пустое множество.

Задача 103. (с решением). Вывести уравнение сферы с центром в точке C(x_o, y_o, z_o радиуса r.

Решение. Сфера есть множество точек, находящихся на расстоянии r от точки C(x_o, y_o, z_o). Введем в пространстве декартову прямоугольную систему координат. Точка M(x, y, z) лежит на сфере S тогда и только тогда, когда длина отрезка CM равна r или тогда и только тогда, когда CM²=r^{2 .} Расстояние между точками M и C равно

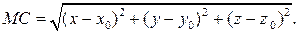
Поэтому уравнение окружности будет иметь вид

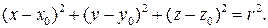
В частности, уравнение сферы радиуса r с центром в начале координат имеет вид:

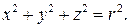
. M(x,y,z)

Z

Mm

O Y

X

Задача 104.(с решением) Выяснить, какие линии получаются при сечении поверхности однополостного гиперболоида

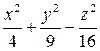
плоскостью x= const, z= const.

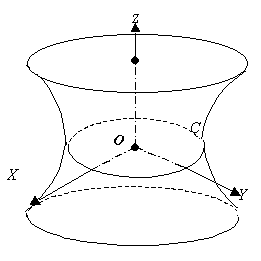
Решение. При z= const = z₀ получаем в сечении эллипс

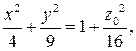
в случае z ₀ = 0 так называемый горловой эллипс

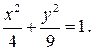
Рассмотрим теперь сечение плоскостью x= const =x₀. Если 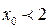, то получаем гиперболу с действительной осью OY

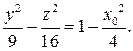
. При x₀=2 получаем уравнение двух прямых., целиком лежащих на поверхности гиперболоида

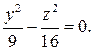
Если 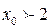, то имеем гиперболу с действительной осью OZ

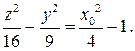
Примечание. В случае, если плоскость координат не параллельна координатной плоскости, для определения вида кривой второго порядка, получающейся в сечении, надо перейти в прямоугольную систему координат, связанную с секущей плоскостью.

Задача 105. Написать уравнение сферы:

1) с центром в точке 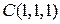и радиусом ;

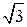2) с центром в точке 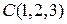и радиусом 1.

Задача 106. Найти ось вращения поверхности, изобразить поверхность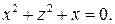

Задача 107. Найти уравнение поверхности, получаемой вращением параболы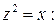

1) вокруг оси 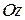; 2) вокруг оси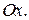

Задача 108. (с решением) Доказать, что уравнение 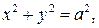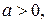в декартовой прямоугольной системе координат является уравнением прямой круговой цилиндрической поверхности 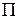с образующими, параллельными оси OZ, причем плоскость XOY пересекает эту поверхность по окружности C радиуса a с центром в начале координат.

Решение.В самом деле, координаты точки M (x,y,z) удовлетворяют уравнению 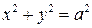тогда и только тогда, когда координаты 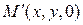проекции точки M на плоскость XOY удовлетворяют этому уравнению, а это значит, что точка M лежит на поверхности, заданной уравнением 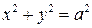тогда и только тогда, когда ее проекция 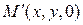на плоскость XOY лежит на окружности C .

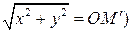Значит, 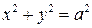есть уравнение цилиндрической поверхности ,

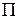описанной выше.

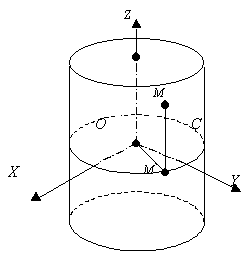
Задача 109. Найти уравнение прямого кругового цилиндра радиуса 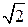с осью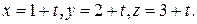

Задача 110. Найти уравнение конуса с вершиной в точке 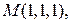касающегося сферы
.

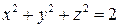Задача 111. Найти уравнение конуса с вершиной в точке 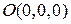и направляющей – окружностью .

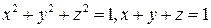Задача 112. Найти прямолинейные образующие параболоида 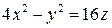, пересекающиеся в точке .

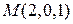Задача 113. Найти центр и радиус окружности

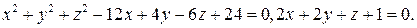
Задача 114. (с решением). Выяснить, какие линии получаются при сечении поверхности однополостного гиперболоида

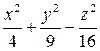
плоскостью x= const, z= const.

Решение. При z= const = z₀ получаем в сечении эллипс

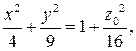
в случае z ₀ = 0 так называемый горловой эллипс

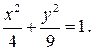
Рассмотрим теперь сечение плоскостью x= const =x₀.. Если 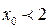, то получаем гиперболу с действительной осью OY

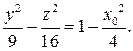
. При x₀=2 получаем уравнение двух прямых., целиком лежащих на поверхности гиперболоида

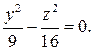
Если 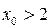, то имеем гиперболу с действительной осью OZ

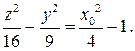
Примечание. В случае, если плоскость координат не параллельна координатной плоскости, для определения вида кривой второго порядка, получающейся в сечении, надо перейти в прямоугольную систему координат, связанную с секущей плоскостью.