Теоретические сведения. В соответствии с теорией Ляпунова [5] об устойчивости движения, невозмущенное движение будет устойчивым

В соответствии с теорией Ляпунова [5] об устойчивости движения, невозмущенное движение будет устойчивым, если после снятия ограниченного по величине возмущающего воздействия отклонение траектории системы в возмущенном движении от траектории в невозмущенном движении не превысит некоторую наперед заданную величину, зависящую от величины возмущения и стремящуюся к нулю при уменьшении возмущения. Если отклонение с течением времени уменьшается до нуля независимо от величины возмущения (траектория в возмущенном движении асимптотически стремится к траектории в невозмущенном движении), то такое движение называется асимптотически устойчивым.

Невозмущенным считают движение системы, вызванное только воздействием заданных сил. Действительное движение при наличии внешних возмущений называют возмущенным. При исследовании устойчивости возмущение определяется как отклонение координат системы в начальный момент времени в возмущенном движении от аналогичных координат в невозмущенном движении.

Применительно к объекту линейной системы управления невозмущенному движению объекта соответствует изменение его выходной величины под воздействием управления. Для системы входным воздействием можно считать задание, выход системы, как правило, совпадает с выходом объекта.

С точки зрения математического описания изменение выхода отражается частным решением дифференциального уравнения системы. Полное решение уравнения описывает возмущенное движение или изменение выходной величины системы, а общее решение - отклонение возмущенного движения от невозмущенного. Как известно, общее решение получают для уравнений с нулевой правой частью, и чтобы промоделировать это решение необходимо получить решение однородного уравнения. Чтобы это решение не было тождественно равным нулю следует задать начальные условия (начальное значение выходной координаты или ее производных) отличные от нулевых. Эти начальные условия являются возмущением. Для моделируемой системы, на вход которой подается нулевой сигнал, а возмущение вводится путем задания ненулевых начальных условий, стремление выхода к некоторой постоянной величине, уменьшающейся с уменьшением начальных условий, говорит о ее устойчивости. Если же эта постоянная равна нулю независимо от величины начального значения выхода, - система является асимптотически устойчивой. Эти выводы справедливы как для разомкнутых, так и для замкнутых систем. Применительно к решению дифференциальных уравнений условие устойчивости частного решения формулируется следующим образом: частное решение будет устойчивым если общее решение при ненулевых начальных условиях, не превышающих некоторой величины, уменьшается до нуля при соответствующем уменьшении начальных условий. Устойчивость будет асимптотической в случае, когда общее решение стремится к нулю при 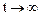. Общее решение будет стремиться к нулю в случае, когда действительные части всех корней характеристического уравнения

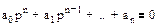(6.4)

отрицательны и 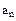, 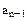не равны одновременно 0.

Оценка устойчивости по модели объекта производится прямым путем непосредственного анализа корней характеристического уравнения, или косвенно на основании алгебраических и частотных критериев [5]. Частотные критерии Михайлова и Найквиста достаточно наглядны и позволяют произвести также оценку запаса устойчивости.

Чтобы оценить устойчивость системы (разомкнутой или замкнутой) по критерию Михайлова следует получить функцию Михайлова путем замены оператора дифференцирования p в левой части характеристического уравнения (6.4) на jw, построить годограф, увеличивая частоту от 0 до значений, при которых действительная и мнимая части функции Михайлова прекращают изменение знаков. Если годограф Михайлова, начинаясь на положительной действительной полуоси, проходит последовательно n четвертей против часовой стрелки - система n – го порядка будет устойчива. Когда годограф выходит из начала координат и попадает во вторую четверть, что происходит при наличии в цепи интегрирующего звена, - система находится на границе устойчивости. Во всех остальных случаях система неустойчива.

Критерий Найквиста позволяет оценить по амплитудно-фазовой частотной характеристике разомкнутой системы устойчивость замкнутой системы, полученной при охвате разомкнутой системы отрицательной единичной обратной связью. Обоснование критерия Найквиста, также как и критерия Михайлова, дано во всех учебниках. Ниже приведена только его формулировка [5] для следующих случаев: - если разомкнутая система неустойчива, то для устойчивости замкнутой системы, необходимо и достаточно чтобы амплитудно-фазовая характеристика разомкнутой системы при изменении частоты от нуля до бесконечности охватывала точку (-1, j0) в положительном направлении (против часовой стрелки) q/2 раз, где q - число корней характеристического уравнения разомкнутой системы, имеющих положительную действительную часть (лежащих в правой полуплоскости);

- если разомкнутая система устойчива, для устойчивости замкнутой системы АФЧХ разомкнутой не должна охватывать точку (-1, j0);

- если разомкнутая система содержит n последовательно соединенных интегрирующих звеньев, то при оценке устойчивости замкнутой системы следует дополнить АФЧХ разомкнутой системы дугой достаточно большого радиуса, начинающейся на положительной действительной полуоси и проходящей по часовой стрелке n четвертей. В случае, когда такая дополненная АФЧХ не охватывает точку (-1,j0) - замкнутая система будет устойчивой.

- если АФЧХ устойчивой разомкнутой системы проходит через точку (-1, j0) - замкнутая система находится на границе устойчивости.

Для примера проведем анализ устойчивости системы, структурная схема которой приведена на рис.6.1.