Двойной интеграл

Рассмотрим в плоскости 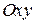замкнутую область 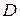. Область 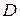называется замкнутой, если она ограничена замкнутой линией, и точки, лежащие на границе, считаются принадлежащими области .

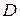Пусть в области 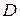задана непрерывная функция .

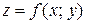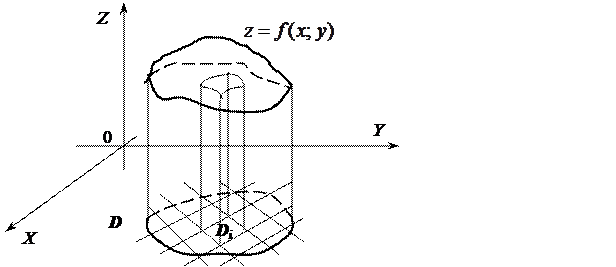
Схема получения двойного интеграла

1) Разбиваем область 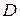на 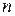«элементарных областей» .

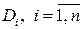2) Площадь области 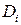обозначим 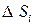, а диаметр (наибольшее расстояние между двумя точками области) – через .

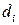3) Возьмем произвольную точку .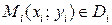

4) Находим 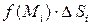, что равно объему тела (призма), площадь основания которого 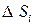, а высота равна .

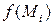5) Составляем интегральную сумму

.

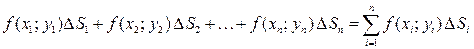6) Обозначим через 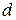длину наибольшего из диаметров «элементарных областей», т.е. 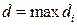, 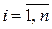. Найдем предел интегральной суммы, когда 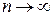так, что 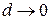. Если предел существует и не зависит от способа разбиения области 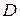на части, ни от выбора точек в них, то он называется двойным интегралом от функции 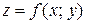по области .

.

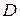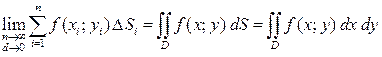Таким образом, двойным интегралом от 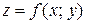по замкнутой областью 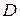называется предел интегральной суммы 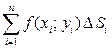, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:

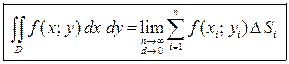. (1.1)

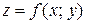- интегрируемая функция в области ;

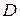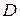- область интегрирования;

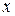и - переменные интегрирования;

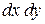или 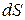- элемент площади.

Для всякой ли функции 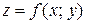существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем без доказательства.