Сравнение нескольких дисперсий

Математическое ожидание и дисперсия генеральной совокупности оцениваются средним и дисперсией выборки тем точнее, чем больше объем выборки. При этом среднее характеризует результат измерений, а дисперсия — точность этого результата (дисперсия воспроизводимости). Если проделано n параллельных опытов (опытов, проведенных при неизменном комплексе основных факторов) и получена выборка y ₁, y ₂, …, y_n значений измеряемой величины, то дисперсия воспроизводимости равна

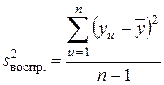, где 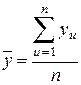, (6.1)

и ошибка опыта (ошибка воспроизводимости)

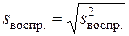(6.2)

Для оценки точности применяемой методики можно поставить специальную серию опытов, многократно повторяя измерение для одного и того же образца. Однако более надежным методом является определение ошибки воспроизводимости по текущим измерениям. Предположим, что выполняются измерения некоторой физической характеристики для k образцов, при этом для каждого образца делается различное число параллельных опытов: n ₁, n ₂, …, n_k. Частные дисперсии для каждой выборки обозначим как 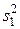, , 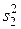…, 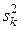. Числа степеней свободы частных дисперсий равны: f ₁ = n ₁ – 1, f ₂ = n ₂ – 1, …, f_k = n_k – 1. Общая дисперсия воспроизводимости всех опытов будет равна средневзвешенному значению частных дисперсий (в качестве весов берутся степени свободы):

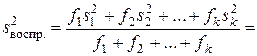
. (6.3)

Число степеней свободы общей дисперсии равно общему числу измерений минус число связей, использованных для определения k средних:

. (6.4)

Если число опытов для каждого образца одинаково (n ₁ = n ₂ = … = = n_k = n), то

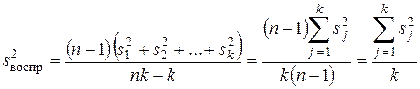, (6.5)

т. е. при равном числе параллельных опытов общая дисперсия воспроизводимости равна среднеарифметическому значению частных дисперсий. Число степеней свободы равно f _воспр. = k (n - 1). Число степеней свободы у общей дисперсии воспроизводимости гораздо больше, чем у каждой дисперсии в отдельности. Поэтому общая дисперсия воспроизводимости намного точнее оценивает дисперсию генеральной совокупности.

При вычислении дисперсии воспроизводимости по текущим измерениям можно объединять между собой только те результаты, которые можно рассматривать как выборки из генеральных совокупностей с равными дисперсиями.

Итак, при определении оценки дисперсии по текущим измерениям

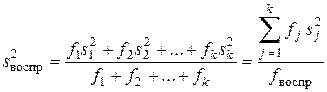(6.6)

принимается нулевая гипотеза равенства соответствующих генеральных дисперсий. Проверить эту гипотезу для выборок разного объема можно по критерию Бартлета. Бартлет показал, что в условиях нулевой гипотезы отношение В / С, где

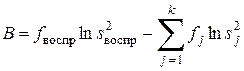, (6.7)

, (6.8)

распределено приближенно как c² с k – 1 степенями свободы, если все f_j > 2. Гипотеза равенства генеральных дисперсий принимается, если при выбранном уровне значимости р

. (6.9)

Различие между выборочными дисперсиями можно считать незначимым, а сами выборочные дисперсии — однородными. Так как всегда С > 1, то при нулевую гипотезу следует принять; если же 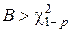, то критерий Бартлета вычисляют полностью.

Если выборочные дисперсии получены по выборкам одинаковых объемов (n ₁ = n ₂ = … = n_k = n), то для их сравнения используют более удобный и точный критерий Кохрена. Кохрен исследовал распределение отношения максимальной выборочной дисперсии к сумме всех дисперсий

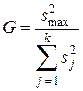(6.10)

Распределение случайной величины G зависит только от числа суммируемых дисперсий k и числа степеней свободы f = n – 1, с которым определена каждая дисперсия.

В приложении 6 приведены квантили G _{1‑ p} для уровня значимости р = 0,05. Если найденное по выборочным дисперсиям значение критерия Кохрена окажется меньше табличного

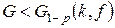, (6.11)

то расхождение между дисперсиями следует считать случайным при выбранном уровне значимости. Если при этом определяется оценка для дисперсии воспроизводимости, то однородные дисперсии можно усреднить.

6.2. Сравнение двух средних.

Расчет средневзвешенного значения.

Для сравнения между собой двух средних, полученных по выборкам из нормально распределенных генеральных совокупностей, применяется критерий Стъюдента.

Пусть заданы две случайные выборки объемами n ₁ и n ₂. Первая выборка взята из нормально распределенной совокупности с параметрами m_x и s _x ², вторая — из совокупности с параметрами m_y и s _y ². По выборкам получены оценки для этих параметров: 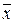, и 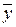, 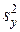. Требуется проверить нулевую гипотезу: m_x = m_y при условии s _x ² = s _y ² = = s². Однородность дисперсий и 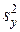проверяется по критерию Фишера. Рассмотрим случайную величину

. (6.12)

По свойству линейности (уравнения 2.37 – 2.38) величина z распределена нормально с параметрами

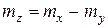, (6.13)

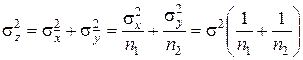. (6.14)

Составим нормированную случайную величину

. (6.15)

При замене генерального стандарта выборочным получается величина, имеющая распределение Стъюдента:

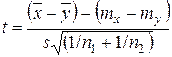, (6.16)

с числом степеней свободы f = n ₁ + n ₂ – 2. В качестве выборочного стандарта используется ошибка опыта, равная

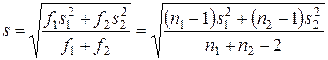. (6.17)

При доверительной вероятности b = 1 – р получаем двустороннюю оценку для разности (m_x - m_y)

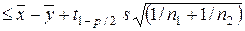(6.18)

или односторонние оценки

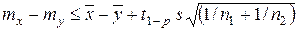, (6.19)

. (6.20)

В условиях нулевой гипотезы m_x = m_y и неравенства (6.18) – (6.20) дают критерий проверки этой гипотезы. Нулевая гипотеза отвергается при двустороннем критерии, если

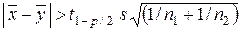, (6.21)

и при одностороннем критерии, если

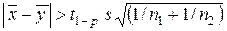. (6.22)

В том случае если выборочные средние являются оценками одного и того же математического ожидания и выборочные дисперсии однородны, то полученные выборки можно объединить в одну серию и рассчитать для нее общие среднее и дисперсию.

Приведенными критериями нельзя пользоваться, если выборочные дисперсии неоднородны (т. е. 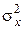¹ 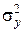). Для этого случая существует несколько приближенных критериев для сравнения двух средних. При n ₁ = n ₂ = n можно воспользоваться приближенным t -критерием:

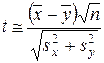(6.23)

с числом степеней свободы 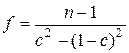, где .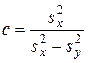

Если число степеней свободы дисперсии равно f ₁ = n ₁ – 1, дисперсии 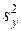— f ₂ = n ₂ – 1, можно использовать другой приближенный критерий. Вычислим величину

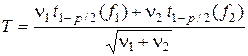, (6.24)

где 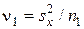и 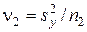. Нулевая гипотеза отвергается, если

.

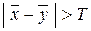Сформулированный критерий является двусторонним, он превращается в односторонний при замене р /2 на р.

При сравнении нескольких средних можно использовать t -крите-рий, проводя сравнение попарно. Если выборочные средние оценивают одно и то же математическое ожидание, то в качестве единственной наилучшей оценки обычно используется средневзвешенное значение. Пусть независимым образом получено k оценок ( j = 1, 2,…, k) некоторой величины Х:

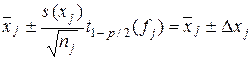. (6.25)

Определим вес результата, полученного в каждой серии опытов:

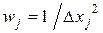. (6.26)

Тогда средневзвешенное значение (наилучшая оценка для Х) равно

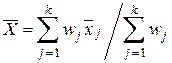, (6.27)

а его погрешность определяется формулой

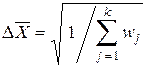. (6.28)

6.3. Проверка однородности результатов измерений.

Грубые измерения являются результатом поломки прибора или недосмотра экспериментатора, и результат, содержащий грубую ошибку, сильно отличается по величине. На этом основаны статистические критерии оценки и исключения грубых измерений. Наличие грубой ошибки в выборке нарушает характер распределения случайной величины, изменяет его параметры, т.е. нарушается однородность наблюдений. Следовательно, выявление грубых ошибок можно трактовать как проверку однородности наблюдений, т. е. проверку гипотезы о том, что все элементы выборки получены из одной и той же генеральной совокупности.

Пусть имеется выборка х ₁, х ₂, …, х_n значений нормально распределенной случайной величины Х. Обозначим через х _max (х _min) наибольший (наименьший) результат измерений. Величины

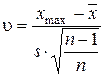, (6.29)

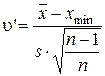(6.30)

имеют специальное распределение, зависящее только от числа степеней свободы f = n – 2. В приложении 7 приведены значения u (u¢) для р = 0,10; 0,05; 0,025 и 0,01 при числе степеней свободы от 1 до 23. Величина х _max (х _min) исключается из выборки как грубое измерение (на уровне значимости р), если определенное по формулам (6.29) и (6.30) значение u или u¢ окажется больше табличного.

Если сомнение вызывают два или три элемента выборки, поступают следующим образом. Для всех сомнительных элементов вычисляют u (u¢), и исследование начинается с элемента, имеющего наименьшее значение u (u¢). Остальные сомнительные элементы из выборки исключаются. Для этой уменьшенной выборки вычисляют 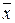, s и новое значение u (u¢) для исследуемого элемента. Если исследуемый элемент является грубым измерением, еще с большим основанием можно считать грубыми ранее исключенные элементы. Если исследуемый элемент не является грубым измерением, его присоединяют к выборке и начинают исследовать следующий по величине u (u¢) элемент выборки, при этом снова вычисляя новые значения 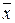, s, и т.д.

6.4. Сравнение выборочного распределения

и распределения генеральной совокупности.

Критерии согласия Пирсона и Колмогорова.

Гипотезу о нормальности изучаемого распределения в математической статистике назыают основной гипотезой. Проверку этой гипотезы по выборке проводят при помощи критериев согласия. Критерии согласия позволяют определить вероятность того, что при гипотетическом законе распределения наблюдающееся в рассматриваемой выборке отклонение вызывается случайными причинами, а не ошибкой в гипотезе. Если эта вероятность велика, то отклонение от гипотетического закона распределения следует признать случайным и считать, что гипотеза о предполагаемом законе распределения не опровергается. Критерий согласия позволяет лишь утверждать, что гипотеза не противоречит опытным данным, если вероятность наблюдаемого отклонения от гипотетического закона велика. Чаще всего используется один из двух критериев согласия: критерий Пирсона (критерий c²) и критерий Колмогорова.

Критерий согласия Пирсона. Для применения критерия c² весь диапазон изменения случайной величины в выборке объема n разбивается на k интервалов (от 8 до 20). Число элементов выборки, попавших в i -интервал, обозначим через n_i. Построенная по этим данным гистограмма выборочного распределения служит основанием для выбора типа закона распределения.

Параметры этого распределения могут быть найдены или из теоретических соображений, или нахождением их оценок по выборке. На основании принятого закона распределения вычисляются вероятности р_i попадания случайной величины Х в i -интервал. Величина, характеризующая отклонение выборочного распределения от предполагаемого, определяется формулой

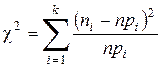, (6.31)

где k — число интервалов; n — объем выборки.

Сумма (6.31) имеет приближенно c²-распределение с f = (k – c – 1) степенями свободы, где с — число параметров гипотетического закона распределения, определяемых по выборке. Для нормального распределения с = 2, если и 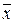, и s определяются по данной выборке.

Гипотеза о принятом типе закона распределения принимается на выбранном уровне значимости р, если 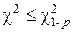, где 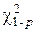— квантиль распределения Пирсона для данного р и числа степеней свободы f (приложение 4). В противном случае делается вывод о том, что гипотеза не согласуется с выборочным распределением.

При использовании критерия c² желательно, чтобы объем выборки был достаточно велик: n ³ 50 ¸ 150, а количество элементов n_i ³ 5 ¸ 8. Вероятности р_i для нормального закона распределения можно определить по формуле

.

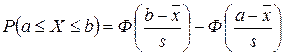При подсчете теоретических вероятностей р_i считается, что крайний левый интервал простирается до -¥; крайний правый — до +¥.

Критерий согласия Колмогорова. Для применения этого критериянеобходимо определить наибольшее абсолютное отклонение выборочной функции распределения F_n (x) от генеральной F (x):

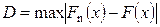, (6.32)

затем вычислить величину l:

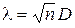. (6.33)

Квантили l_{1- р} распределения Колмогорова приведены в приложении 8. Если l < l_{1- р} , то гипотеза о совпадении теоретического закона распределения F (x) с выборочным F_n (x) не отвергается. При l ³ l_{1- р} гипотеза отклоняется (или считается сомнительной). Уровень значимости при применении критерия Колмогорова выбирают обычно равным 0.2 ¸ 0.3.

Для нормального распределения F (x) определяется по формуле

.

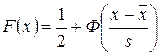В случае выборок небольшого объема (n < 20) для проверки гипотезы о законе распределения можно использовать простые критерии, основанные на сравнении генеральных параметров распределения и их оценок, полученных по выборке. В качестве оцениваемых параметров удобнее всего брать моменты.

ПРИЛОЖЕНИЯ