Теорема: Для устойчивости ЛДС (1) при любой правой части f(t) необходимо и достаточно, чтобы было устойчивым тривиальное решение соответствующей однородной системы (2)

Доказательство:

Þ Пусть 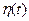некоторое устойчивое решение системы (1), 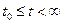. Значит "e>0 $d(e)>0: " 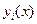- решения системы (1) при 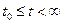будет справедливо неравенство:

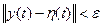(3)

если выполняется 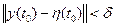(4)

Но если y и h решения (1), то

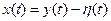(5)

решение однородной системы (2).

Любое решение однородной системы всегда можно представить в виде (5). Соответственно по (3) и (4) получаем, что 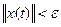если 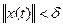. Это выполняется " x(t), значит выполнится и для х₀=0, т.е. тривиальное решение однородной системы (2) устойчиво по Ляпунову при 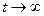.g

Замечание. Из доказательства следует, что устойчивость тривиального решения системы (2) вытекает из устойчивости хотя бы одного решения линейной неоднородной системы (1) при любой правой части f(x), которая может быть даже тождественно равна 0.

Ü Пусть х₀=0 – тривиальное решение однородной системы (2). И пусть х₀ устойчиво по Ляпунову при 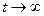, тогда, если x(t) произвольное решение однородной системы (2): 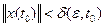выполняется при условии, что 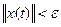. Пусть 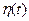, y(t) некоторые произвольные решения системы (1), тогда из 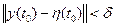будет следовать, что 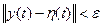" 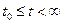(это следует из определения x(t)). Последние два неравенства означают, что 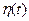будут устойчивыми по Ляпунову при .

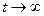Следствие. ЛДС устойчива, когда устойчиво хотя бы одно решение этой системы, и вполне не устойчива, если неустойчиво ее некоторое решение.

Следствие. Неоднородная ЛДС устойчива тогда и только тогда, когда устойчива соответствующая ей однородная.

Замечание. Поведение решений неоднородной ЛДС (1) при любой правой части совпадает с поведением решений соответствующей однородной системы (2), следовательно, далее мы будем исследовать на устойчивость только однородную систему (2).

Определение: ЛДС (1) называется равномерно устойчивой, если все решения этой системы равномерно устойчивы при .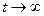

Теорема. ЛДС (1) равномерно устойчива тогда и только тогда, когда тривиальное решение соответствующей ей однородной системы (2) равномерно устойчиво при .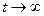

Определение. ЛДС (1) называется асимптотически устойчивой, если все ее решения асимптотически устойчивы.

Теорема. Система (1) асимптотически устойчива тогда и только тогда, когда тривиальное решение соответствующей системы (2) асимптотически устойчиво при .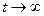

Следствие. Для асимптотической устойчивости системы (1) при любой правой части необходимо и достаточно, что бы была асимптотически устойчива система (2).