Многомерные слУчайные величины

СОДЕРЖАНИЕ

1. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.......................................

2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МНОГОМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН....................................................................................................

3. ЗАКОН РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН.....

4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН......................................................................................................................

5. ОЦЕНКА ЗАКОНА РАСПРЕДЕЛЕНИЯ...................................................

5.1. Эмпирическая функция распределения...................................................

5.2. Гистограмма распределения случайной величины................................

6. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ И ЧИСЛОВЫХ ХАРАКТЕРИСТИК.....................................................................................

6.1. Примеры точечных оценок......................................................................

6.2. Методы получения оценок параметров распределения.........................

7. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ЧИСЛОВЫХ ХАРАКТЕРИСТИК............

8. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ..........................................

8.1 Критерий согласия 2...............................................................................

8.2. Критерий согласия Колмогорова............................................................

8.3 Проверка гипотезы об отсутствии корреляционной зависимости..........

9. ОЦЕНКА КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ...................

ЛИТЕРАТУРА.................................................................................................

ПРИЛОЖЕНИЕ...............................................................................................

Многомерные слУчайные величины

Основные свойства многомерных случайных величин рассмотрим на примере двумерных случайных величин.

Функией распределения двумерной случайной величины называ­вается вероятность совместного выполнения двух событий { Х < х } и { Y < у }:

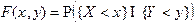. (1.1)

Свойства двумерной функции распределеия:

1. 0 F (x, y) 1.

2. F (x, +) = F 1(x); F (+, y) = F 2(у); F (+,+) = 1.

3. F (-, y) = F (x, -) = F (-, -) = 0.

4. F (x 1, y) F (x 2, y), если x 2> x 1;

F (x, y 1) F (x, y 2), если y 2> y 1.

Функция распределения может задаваться для непрерывных и дискретных случайных величин.

Для непрерывных случайных величин существует плотность распределения или дифференциальный закон распределения:

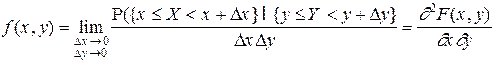. (1.2)

Свойства двумерной плотности.

1. f (x, y) 0.

2. 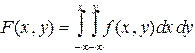. (1.3)

3. 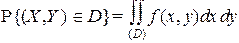. (1.4)

4. Условие нормировки

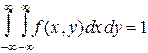. (1.5)

5. ; . (1.6)

Для дискретных случайных величин (X, Y) закон распределения задается матри­цей вероятностей, содержащей вероятности pij появления всех возмож­ных пар значений (xi, yj):

pij = P(X =x_i, Y = y _j ), (1.7)

удовлетворяющих условию

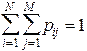. (1.8)

Одномерные ряды вероятностей составляющих X, Y определяются по формулам

; (1.9)

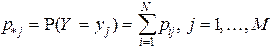. (1.10)

Условным законом распределения называется распределение одной случайной величины, найденное при условии, что другая случайная величина приняла определенное значение.

Условные плотности для непрерывных составляющих X и Y определяются по формулам:

f (x / y) = f (x, y)/ f 2(y), f ₂ (y)¹ 0; (1.11)

f (y / x) = f (x, y)/ f 1(x), f ₁ (x)¹ 0. (1.12)

Условные ряды вероятностей для дискретных составляющих Х и Y определяются по формулам:

pi / j = P(X = xi / Y = yj) = pij /P(Y = yj), i = 1,..., N; (1.13)

pj / i = P(Y = yj / X = xi) = pij /P(X = xi), j = 1,..., M. (1.14)

Теорема умножения законов распределений:

-для непрерывных величин

f (x, y) = f 1(x) f (y / x) = f 2(y) f (x / y); (1.15)

-для дискретных величин

. (1.16)

Условия независимости случайных величин:

-для непрерывных

f (x, y) = f 1(x) f 2(y), (1.17)

-для дискретных

pij = pi pj, для i, j. (1.18)

Пример 1.1. Двумерная случайная величина (X, Y) распределена по закону, приведенному в таблице:

	xi
yj	x 1= 0	x 2= 0
y 1= -1	0,1	0,2
y2= 0	0,2	0,3
y3= 1		0,2

Определить одномерные ряды вероятностей величин X и Y, условный ряд вероятностей величины X при условии, что Y = 0. Исследовать зависимость случайных величин X и Y.

Решение. Определим ряды вероятностей X и Y по формулам (1.9) и (1.10), т.е. выполним суммирование по столбцам и по строкам:

xi				yj	-1
pi *	0,3	0,7		p * j	0,3	0,5	0,2

Условный ряд X при Y = 0 получаем по формуле (1.13):

xi
pi / Y =0	0,4	0,6

Величины X и Y зависимы, так как P(X = 0, Y = 0) P(X = 0)P(Y = 0),
0,2 0,3 0,5.

Пример 1.2. Иглу длиной b бросают на плоскость, на которой на расстоянии L друг от друга проведены параллельные линии. Определить вероятность пересечения иглой одной из линий, если b < L (задача Бюффона).

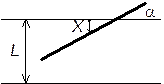
Решение. Рассмотрим двумерную случайную величину (X,), где X -расстояние от середины иглы до ближайшей линии, - острый угол между иглой и линией.

Составляющая X распределена равномерно в интервале [0; L /2], а распределена равномерно в интервале [0; /2]. Тогда плотность распределения составляющей X: f 1(x) = 2/ L, а составляющей: f 2() = 2/.

Согласно теореме умножения законов распределений (1.15) двумерная плотность равна f (x,) = (2/ L)(2/). Пересечение иглой одной из линий для заданного угла будет, когда 0 < X < (b /2)sin.

Тогда

.

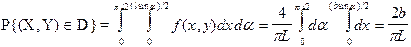ЗАДАЧИ

1.1. В двух ящиках находятся по шесть шаров; в первом ящике: один шар с номером 1, два шара с номером 2, 3 шара с номером 3. Во втором ящике: два шара с номером 1, три шара с номером 2, один шар с номером 3. Пусть X номер шара, вынутого из первого ящика, Y номер шара, вынутого из второго ящика. Из каждого ящика вынули по шару. Составить матрицу вероятностей двумерной случайной величины X, Y. Найти одномерные ряды распределений составляющих X и Y.

Y X	x 1=1	x 2=2	x 3=3
y 1=2	1/18	1/9	1/6
y 2=3	1/12	1/6	1/4
y 3=1	1/36	1/18	1/12

Ответ:

Одномерные ряды составляющих X и Y:

X	x 1=1	x 2=2	x 3=3		Y	y 1=2	y 2=3	y 3=1
	1/6	1/3	1/2			1/3	1/2	1/6

1.2. Двумерная случайная величина имеет закон распределения с плотностью

.

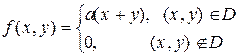Область D - квадрат, ограниченный прямыми x = 0, x = 3, y = 0, y = 3.

Требуется определить коэффициент a; вычислить вероятность попадания случайной точки (X, Y) в квадрат Q, ограниченный прямыми x = 1, x = 2, y = 1, y = 2.

Ответ: a = 1, P = 1/9.

1.3. Двумерная случайная величина распределена по закону:

.

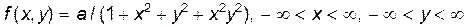Найти коэффициент а, установить зависимость случайных величин X и Y.

Ответ: a = 1/2, независимы.

1.4. Имеются две независимые случайные величины (X, Y), распреде­ленные по показательному закону:

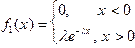
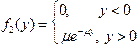
Найти f (x, y), F (x, y).

Ответ: ; .

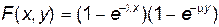1.5. Положение случайной точки (X, Y) равновозможно в любом месте круга радиусом R, центр которого совпадает с началом координат. Определить плотность распределения и функцию распределения каждой составляющей X и Y. Выяснить зависимость X и Y.

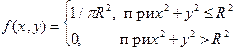
Ответ: 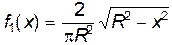, , 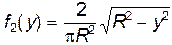X и Y независимы.