Критический уровень процентной ставки

Предположим, что имеется финансовое обязательство вы­платить 200 тыс. руб. (FV\) через 3 месяца (п\), которое впослед- ' ствии заменяется на другое обязательство - выплату 250 тыс.; руб. (FV2) через 6 месяцев (иг). Как видно из условия, фиксиро- ^ ванными величинами являются размеры и сроки платежей.

Возникает вопрос: могут ли два указанных платежа быть эквивалентными? Если могут, то при каких условиях? Условием эквивалентности в данном случае является определенный уро­вень процентной ставки, учитываемой в расчетах. Уровень про­центной ставки, при котором платежи являются эквивалентны- | ми, называется критическим или барьерным.

Нахождение критической ставки основывается на приве- | денных выше уравнениях эквивалентности, в которых неизвест- | ной величиной является процентная ставка. Рассмотрим это | уравнение для случаев простой и сложной ставок.

Простая процентная ставка. Исходное уравнение эквива- I лентности может быть записано на основе равенства современ- | ных стоимостей двух платежей:

FVS x

FV,-FV₂ = i_bx(FV₂xn_}-FV,Xn₂);

h = (^FV\ ~ ^FV2) *(РУ₂ ^x "i ~ ^FVi ^x "2) ■ (2.2.24)

Разделив числитель и знаменатель правой части равенства на (-FV1), получим:

Для рассматриваемого примера имеем:

При такой ставке данные обязательства будут эквивалент­ными.

Для сложных процентов уравнение эквивалентности запи­шется в виде:

FV, _ FV₂

Проведем несложные алгебраические преобразования:

-1. (2.2.26)

Сравниваются два платежа:

1)4 тыс. руб. с выплатой через 3 года;

2)6 тыс. руб. с выплатой через 4 года.

h=ⁱ⁴-³j~~l = 1,5-1 = 0,5; i = 5O%.

Если в расчетах учитывается ставка 50% годовых, то рас­сматриваемая замена платежей не нарушает принципа их экви­валентности.

Каким образом отклонение фактически действующей став­ки от критической влияет на предпочтительность конверсии платежей для получателя или плательщика?

Если

'FV,

то осуществляется неэквививалентная замена, которая ставит в выгодное положение плательщика денежной суммы. Это вытека­ет из того, что в данном случае PV_{ > PV₂. В случае, когда

ситуация иная: преимущества имеет получатель. Такое положе­ние является следствием того, что PV^ < PV₂.

Обратимся к данным приведенного выше примера. Если уровень процентной ставки ниже критического уровня, то совре­менная стоимость первого платежа будет меньше второго. На­пример, в расчетах используется ставка в размере 20% годовых. Современные стоимости платежей будут:

PV_l =4х(1 + 0,2)"⁵ = 2,3 тыс. руб.; PV₂ =6x(l + 0,2)-⁴ =2,89 тыс.руб. Таким образом, PV_i < РУ_г.

Консолидация платежей

Консолидация платежей - это объединение нескольких платежей в один. Консолидацию можно считать частным случа­ем конверсии. Сумма заменяемых платежей должна быть экви­валентна одному заменяющему платежу.

Пусть мы имеем серию платежей в размерах FV_U FV2, FV$,..-, FV_m с соответствующими сроками п\, /12, щ, п_т. Заменяем эту серию платежей на один платеж в размере FVq со сроком уплаты п₀.

В этом случае возможны две постановки задачи: если зада­ется срок «о, то находится сумма -Si), и наоборот, если задана сумма консолидированного платежа Sq, to определяется срок но-Рассмотрим обе постановки задачи.

Ддя определения размера консолвдированного платежа рассмотрим два варианта.

1. Срок щ находится внутри ряда П[, ni, «з> - "т> ^т- ^е-
Л1<и_о<и,„. Пронумеруем платежи в интервале щ + щ по j{FV_p
«_у), а в интервале «o⁺"m по к{РУь\ "*)■ Тогда разница в сроках
определится так: t_} = п$ - n_}; t_k = n_k - щ.

Далее необходимо привести все платежи к единой времен­ной точке. Возьмем в качестве такой точки время уплаты консо­лидированного платежа. В этом случае сумму FVq можем опре­делить по формуле:

FV_t =J_jFV_ix(l + t_Jxi) + J_jFV_ix(\ + t_t-iy' - (2.2.27)

Первое слагаемое правой части характеризует процессы наращения размеров платежей первоначальной серии, сроки уп­латы которых должны были наступить раньше срока консолиди­рованного платежа. Второе слагаемое, напротив, выражает про­цессы дисконтирования размеров платежей, сроки которых наступают позже срока консолидированного платежа.

2. Для срока ло верно:»о > "т ■

В этом случае консолидированный платеж производится позже последнего платежа первоначальной серии, поэтому в расчете присутствует лишь одна операция наращения:

FV₀ = Y_JPV_J x (1 + t_J xi) - (2.2.28)

Сложные процентные ставки. При сохранении обозначе­ний, введенных для простой ставки, имеем следующее уравне­ние эквивалентности:

Определение срока консолидированного платежа

Если сумма консолидированного платежа FVq задана, воз­никает задача определения его срока. Уравнение эквивалентно­сти записывается в виде равенства современных стоимостей уча­ствующих в расчетах платежей:

FV (1 + /хи)"' = Т¹ FV хО + и х/)"' (2 2 30)

Проведя алгебраические преобразования, получим:

(2.2.31)

Сложная процентная ставка. Если в расчетах используется сложная процентная ставка, то уравнение эквивалентности име­ет вид:

FV^ х{1 + /)"• = £ FV_J х (1 + /р ■ (2.2.32)

Проведя алгебраические преобразования, получим:

1п(1 + 0

Эквивалентность процентных

В условиях, когда имеются различные варианты размеще­ния финансовых ресурсов, важно соблюсти описанный выше принцип эквивалентности Например, вкладчик рассматривает возможности размещения одной и той же суммы на депозите: в одном случае по простой ставке, в другом — по сложной. Пред­положим, перед ним стоит задача получить одинаковые финан­совые результаты от упомянутых альтернатив. Какие процентные ставки при этом следует использовать? Или допустим, что банк хочет определить эффективность учетной операции, для чего ему необходимо перейти от учетной ставки к ставке наращения.

Различные процентные ставки, обеспечивающие равные финансовые результаты, называются эквивалентными.

Эквивалентность простых ставки наращения(4) и учетной ставки (d_s).

При выводе искомых соотношений следует иметь в виду, что при применении этих ставок используется временная база К = 60 или К = 365 дней. Исходное уравнение эквивалентности в данном случае имеет вид:

wi+,-«) = —. <2-2.34)

Осуществив простые преобразования, получаем:

I = ^Р; (12.35)

(2.2.36)

Если период осуществления финансовой операции меньше года, то n = tlK (/ —продолжительность финансовой операции, К — временная база, или расчетная продолжительность года). Формулы соответствующим образом модифицируются (для слу­чая равенства временных баз):

' K~lxd

(2.2.37)

d = ^Kxi-. (2.2.38)

³ ^+(xi*

Эквивалентность простых и сложных ставок наращения при начислении процентов - один раз в году. Уравнение экви-. валентности запишется так:

где i_s— простая ставка наращения;

/_е — сложная ставка наращения, т. е.:

(2.2.39) (2.2.40)

Эквивалентность сложной номинальной ставки при начис­лении процентов т раз в году и простой ставки:

(2.2.41)

у = ("ф + i_!xn - 1)х т. (2.2.42)

Эквивалентность сложной номинальной ставки при начис-, лении процентов т раз в году и годовой сложной ставки:

i_e=>(l + y/m)^m~l. (2.2.43)

Видно, что данная формула совпадает с формулой расчета эффективной ставки.

Эквивалентность сложных учетной ставки и ставки нара­щения:

i_t=*dj{\-d_t), (2.2.44)

d_c=i_c!(\ + i_c), (2.2.45)

где d_c - сложная учетная ставка.

Эквивалентность дискретных и непрерывных ставок. С уче­том формулы определения наращенной суммы при непрерывном начислении процентов уравнение эквивалентности выгладит так:

отсюда:

i,=e<-\; (2.2.46)

Средние процентные ставки. Разновидностью эквивалент­ных ставок являются средние ставки. Средняя ставка является эквивалентной серии ставок, для которых определяется эта средняя, т. е. замена нескольких ставок их средней не меняет результата финансовой операции. Среди множества различных вариантов возможны следующие сравнительно простые случаи постановки проблемы определения средних ставок.

Нахождение средней процентной ставки за период, со­стоящий из подпериодов с известными размерами ставок за ка­ждый подпериод.

Для простой ставки уравнение эквивалентности:

Рх(1 + #хО =.Рх(1 + ]£и,Х(Д ■ (2.2.48)

где N = £н*, щ — длительность А-го периода времени, в течение которого действует процентная ставка i*;

< - средняя процентная ставка.

Найденный показатель представляет собой среднюю

арифметическую взвешенную с весами, равными продолжитель-, ности отдельных периодов.

Для сложной ставки уравнение эквивалентности имеет вид:

Px(l + if =Fx(l + /_l)"'x(I + /₂)"'..., (2.2.49)

i = ^(1 + (_|)-'х(1+(,)'"... -1. (2.2.50)

Средняя в этом случае вычисляется как взвешенная сред­няя геометрическая.

Определение средней ставки для нескольких операций, перио­ды проведения которых одинаковы. Рассмотрим уравнения экви­валентности:

а) для простых процентных ставок:

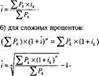
(2.2.51)

(2.2.52)