Оценивание параметров эконометрической модели с учетом ограничений

При нахождении оценок параметров линейной эконометрической модели с использованием МНК предполагалось, что их значения не связаны никакими ограничениями. Вместе с тем, исходные предпосылки, лежащие в основе некоторых моделей, описывающих реальные социально-экономические процессы, предполагают, что значения их параметров не могут быть произвольными. Как это будет показано в следующих разделах, часто “содержательными” являются модели только с положительными значениями параметров, Такая ситуация характерна, например, для моделей, описывающих зависимость выпуска продукции от капиталовложений. При их построении предполагается, что влияние капиталовложений любого предыдущего периода на выпуск продукции в текущем периоде может быть только положительным. В этом случае при оценке параметров должны приниматься во внимание естественные ограничения типа

a_i >0. (2.80)

В ряде моделей в качестве исходных допущений выдвигаются определенные соотношения между значениями параметров. Так в классическом варианте производственной функции Кобба-Дугласа (1.17) условие постоянной отдачи от факторов требует, чтобы сумма коэффициентов при них равнялась единице, т. е. a ₁+ a ₂=1, при сохранении условия (2.80) для каждого из них. Ограничения в виде соотношений между значениями параметров называют линейными. В общем случае они могут быть представлены в векторно-матричной форме записи

R×a = r, (2.81)

где r – известный вектор-столбец, состоящий из k элементов, k < п +1; R – известная матрица порядка k ´(п +1). Ее элементы формируются с учетом конкретного вида линейных взаимосвязей между параметрами модели.

Так, например, если в модели предполагается, что a ₂= a ₃ и a ₂+ a ₃+2 a ₄=2, то вектор r и матрица R имеют следующий вид:

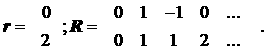
В общем случае постановка задачи оценки коэффициентов эконометрической модели с учетом ограничений с критерием минимума суммы квадратов ошибки формулируется следующим образом: найти параметры a_i, i =0, 1,..., п, минимизирующие квадратическую функцию следующего вида:

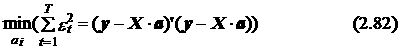
при ограничениях

где 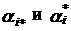– соответственно нижняя и верхняя границы области существования значений параметра a_i.

Заметим, что в постановке (2.82)–(2.84) оценки параметров модели обычно определяются в ходе решения задачи оптимизации (минимизации) квадратической целевой функции при линейных ограничениях с использованием вычислительных процедур итеративного характера. Методы решения таких задач рассмотрены в главе XI.

Вместе с тем, если принимается во внимание только одно ограничение, выраженное соотношением (2.84), то оценки параметров эконометрической модели могут быть получены в аналитической форме. Рассмотрим процедуру получения такого решения с использованием МНК.

Требуется определить вектор оценок параметров 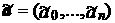модели 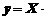a + e, минимизирующий квадратическую функцию

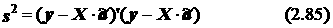
при ограничении (2.84) с использованием исходных данных, представленных в виде вектора-столбца наблюдаемых (известных) значений зависимой переменной у и матрицы наблюдаемых значений независимых факторов Х. Здесь 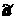означает вектор оценок параметров модели с ограничениями.

Аналитическое решение данной задачи может быть получено с использованием метода множителей Лагранжа. Функция Лагранжа в этом случае записывается в следующем виде:

^{m ¢}

где m – вектор множителей Лагранжа, образованный k элементами (k – количество ограничений).

Условие минимума функции j по аргументу 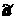имеет традиционный вид

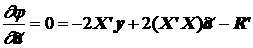^{m (2.87)}

или

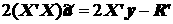^{m . (2.88)}

Умножив правую и левую части выражения (2.88) слева на R ×(X ¢ X)^–1, получим

^{m . (2.89)}

Заметим, что = a, где a – оценка МНК, полученная без учета ограничений. Принимая также во внимание, что 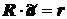, вектор множителей Лагранжа m определим на основе следующего выражения:

^{m = 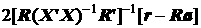. (2.90)}

Подставив (2.90) в (2.87), получим

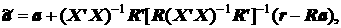^(2.91)

где a, напоминаем, – вектор параметров той же модели, но рассматриваемой без ограничений.

Заметим, что в выражении (2.91) все матрицы и вектора известны, и, таким образом, вектор оценок коэффициентов модели с ограничениями 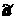определяется непосредственно.

Определим традиционным образом вектор ошибки модели с ограничениями:

Добавив и вычтя в правой части выражения (2.92) слагаемое Xa, получим выражение, связывающее ошибки обоих вариантов моделей в следующем виде:

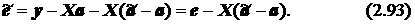
Из выражения (2.93) непосредственно следует, что сумма квадратов ошибки модели с ограничениями определяется следующим образом:

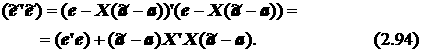
При выводе выражения (2.94) учтено, что X ¢ e = e ¢ X = 0 в силу свойства ошибки (2.44).

Вектор ошибок оценок параметров 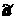найдем, подставив в (2.91) вместо вектора a выражение 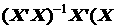a + e), где a и e – векторы параметров и ошибки истинной модели. В результате получим

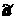= a + Р 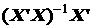× e, (2.95)

где Р – матрица, определенная следующим выражением:

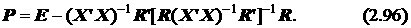
Таким образом,

D 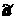= 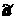– a = Р 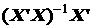× e (2.97)

является вектором ошибок оценок параметров линейной эконометрической модели с учетом наложенных на них ограничений в вида равенств (типа (2.84)).

Поскольку M [ Р 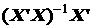× e ]= Р 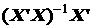× M [ e ]=0, то при отсутствии корреляционных взаимосвязей между переменными х_it и ошибкой e_t полученные оценки 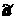являются несмещенными, т. е.

M [ 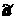]= a. (2.98)

Их ковариационная матрица определяется следующим выражением:

Сov ( 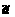)= M [( 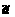– a)( 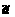– a)]= M [ Р 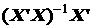× e × e ¢× 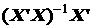× Р ¢]=

= s ² Р 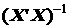× Р ¢. (2.99)

С учетом вида матрицы Р (см. (2.96)) также несложно доказать справедливость следующего равенства^*:

Р 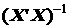× Р ¢= Р 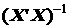. (2.100)

В результате ковариационная матрица оценок параметров линейной эконометрической модели с учетом наложенных на нее ограничений в виде равенств ( 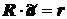) определяется следующим выражением:

Сov ( 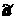)= s ² Р 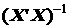. ^(2.101)

В практических исследованиях, как и ранее, дисперсия “идеальной” модели 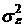заменяется ее оценкой 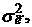рассчитанной с использованием фактических значений ошибки согласно известной формуле

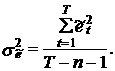
На основании выражения (2.94) несложно оценить также “потери” в точности аппроксимации известных значений зависимой переменной у_t, t =1,2,..., T; при использовании эконометрической модели с ограничениями на параметры вместо модели без таких ограничений. Подставляя в (2.94) вместо разности оценок 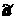– a ее выражение из формулы (2.91), после очевидных упрощений получим

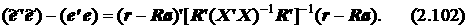
Левая часть выражения (2.102) представляет собой разницу между суммами квадратов ошибок моделей с ограничениями на параметры и без ограничений.