Тестирование свойств фактической ошибки эконометрической модели

На практике справедливость предпосылок (2.21) и (2.22) можно подтвердить или опровергнуть только путем анализа свойств фактической ошибки е_t, после оценки ее значений. В таком случае фактическая ошибка рассматривается как оценка истинной ошибки и выполнение для нее этих предпосылок может рассматриваться в качестве доказательства их обоснованности, а, следовательно, и достаточно высокого качества оценок параметров эконометрической модели.

Заметим, что условие (2.21) s_e ² = const нельзя интерпретировать как постоянство значений ½ e_t ½ для t =1, 2,..., Т. Оно лишь означает, что дисперсия истинной ошибки e_t является постоянной величиной на любом из отрезков рассматриваемого временного интервала (1, Т). В этой связи проверка условия (2.21) может быть идентична проверке гипотезы о постоянстве дисперсии фактической ошибки е_t на различных отрезках интервала (1, Т). Такая проверка обычно проводится с использованием соответствующих тестов.

1. Тестирование условия постоянства дисперсии ошибки модели.

Проверку гипотезы s_e ²=const (выражение (2.21)) можно провести с использованием расчетных значений ошибки е_t на основе, например, двустороннего критерия Фишера. Общая схема реализации процедуры такой проверки состоит в следующем. Интервал (1, Т) разбивается на три интервала (1, Т ₁), (Т ₁+1, Т ₂), (Т ₂+1, Т). При этом первый и третий интервалы обычно выбираются одинаковой длины. В моделях со статической информацией соответственно на три группы разбивается исходная совокупность объектов, которые в данном случае должны быть расположены в порядке возрастания (или убывания) результирующей переменной y_t. Для данных, соответствующих первому и третьем интервалам, строятся эконометрические модели, аналогичные исходному варианту. Для каждой из них определяются последовательности ошибки е_t – е ₁, е ₂,..., и 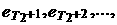е_Т соответственно.

Для первого и третьего интервалов на основании известных значений ошибки, рассчитываются дисперсии

s _{1 e} ²=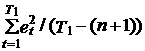

и

s _{3 e} ² =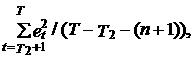

где n – число параметров модели.

Отношение s _{3 e} ² / s _{1 e} ² сопоставляется с граничными значениями двухстороннего критерия Фишера F_* и F^* с заданным уровнем доверительной вероятности р_* и числом степеней свободы n ₁= T –(n +1) и n ₂= T – T ₂–(n +1). Если оказывается, что выполняется соотношение

F_* £ s _{3 e} ² / s _{1 e} ² £ F^*, (2.49)

где, то гипотеза о постоянстве дисперсии на интервале (1, Т) принимается. В противном случае – эта гипотеза отвергается.

Напомним, что F_* =1/ F^* (n ₂, n ₁).

В целом, надежность проверки гипотезы (2.21) по рассмотренной процедуре зависит от правильности выбора числа измерений на каждом из интервалов. С одной стороны, уменьшение их длины приводит к потере точности в оценках s _{1 e} ² и s _{3 e} ² , с другой – ее увеличение может сделать данные оценки статистически неразличимыми, поскольку колебания квадратов ошибок будут уравновешиваться на расширенных интервалах, и значения их дисперсий с ростом Т сблизятся.

Если количество измерений Т достаточно велико, то для проверки гипотезы о постоянстве дисперсии может быть использован критерий Бартлетта. В этом случае интервал (1, Т) разбивается на k участков. По данным каждого из них формируется собственный вариант эконометрической модели, по форме (т. е. по используемым переменным и характеру их взаимосвязей) тождественный вариантам других участков. Для каждого варианта определяется значение дисперсии ошибки s ₁², s ₂²,..., s_k ². Гипотеза постоянства дисперсии предполагает, что s ₁²= s ₂²=...= s_k ²= s ². Если эта гипотеза верна, то усредненная оценка дисперсий s_i ², i =1,2,..., k, рассчитываемая как

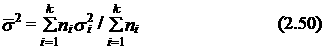
распределена как выборочная дисперсия, т. е. по нормальному закону со средним значением s ² и Т степенями свободы, где Т = 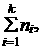n_i – количество измерений на i -м участке.

Бартлетт показал, что величина

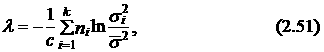
где

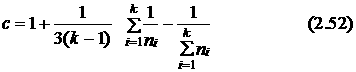
распределена примерно по закону c ² с k –1 степенями свободы.

Для частного случая, когда количество измерений на всех участках равны, т. е. n ₁= n ₂=...= n_k

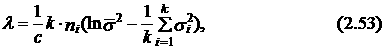
где с =1+[(k +1)/3 k × n_i ].

Таким образом, проверка гипотезы о постоянстве дисперсии эконометрической модели на интервале (1, Т) состоит в сопоставлении расчетного значения c ², определяемого по формуле (2.51) или (2.53), с табличным значением этого критерия c ² _*, взятым при заданной доверительной вероятности р_* и k –1 степенях свободы. Если оказывается, что c ²= l £ c ² _*, то гипотеза о постоянстве дисперсии принимается, если l > c ² _*, то рассматриваемую гипотезу следует отвергнуть.

2. Тестирование автокорреляционной зависимости ошибки.

Проверка выполнимости условия (2.22), свидетельствующего об отсутствии автокорреляционных взаимосвязей в ряду “истинной” ошибки модели e_t, на практике осуществляется путем тестирования ряда значений фактической ошибки e_t.

При этом предполагается, как и в случае тестирования условия (2.21), что свойства фактической ошибки в значительной степени соответствуют свойствам ее теоретического аналога. В данном случае имеется в виду характер автокорреляционных взаимосвязей между значениями ошибок в моменты времени t и t –1, t и t –2 и т. д.

Обычно у случайного процесса (если отсутствуют сезонные эффекты) наиболее существенны взаимосвязи между соседними значениями. Это выражается в том, что абсолютное значение его первого коэффициента автокорреляции превосходит аналогичные значения его коэффициентов автокорреляции более высоких порядков. Вследствие этого проверка выполнимости условия (2.22) часто рассматривается как проверка гипотезы о значимости именно первого коэффициента автокорреляции фактической ошибки. Один из таких тестов (по критерию Дарбина-Уотсона) был рассмотрен в разделе (1.4). Этот тест не отличается значительной достоверностью. Область существования его значений содержит достаточно обширную зону неопределенности, в случае попадания расчетного значения критерия Дарбина-Уотсона в которую нельзя сделать однозначный, статистически обоснованный вывод о наличии или отсутствии автокорреляционной связи у рассматриваемого процесса. Вместе с тем математическая статистика разработала большое количество значительно более мощных тестов, которые могут быть использованы в этих целях. Многие из них рассмотрены в главах VI и VII при тестировании свойств временных рядов.

В данном разделе рассмотрены проблемы тестирования наличия или отсутствия автокорреляционных связей путем проверки гипотезы о значимости непосредственно расчетного значения первого коэффициента автокорреляции фактической ошибки e_t. На первый взгляд, это – наиболее очевидный и прямой путь при проверке гипотезы о наличии автокорреляционной связи в ряду ошибки e_t. Однако на этом пути исследователю приходится сталкиваться с достаточно сложными проблемами. Дело в том, что закон распределения выборочного коэффициента корреляции по форме достаточно сложен и зависит от абсолютного значения r^* и числа измерений Т. При ½ r ½® 0 плотность распределения f (r) симметрична, но с ростом абсолютного значения этого коэффициента она становится резко асимметричной, особенно при небольших значениях Т. Вследствие этого традиционные тесты проверки значимости параметров, использующие предположение о “нормальности” закона распределения их ошибок, в данной ситуации следует применять с определенной осторожностью, особенно в малых по объему выборках.

На практике проверку значимости выборочного коэффициента автокорреляции ошибки r ₁ можно провести двумя способами. Во-первых, можно пренебречь погрешностями, обусловленными отличием закона распределения выборочного коэффициента автокорреляции от нормального, тем более, что при r ₁®0 они не столь значительны. Тогда процедура проверки значимости этого коэффициента сводится к сопоставлению расчетного значения его критерия Стьюдента

с его табличным значением t_* (р_*, Т –2), взятым при заданном уровне доверительной вероятности р_* и известном числе степеней свободы Т –2. В выражении (2.54) 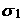характеризует среднеквадратическую ошибку выборочного коэффициента корреляции, величину которой приблизительно можно определить на основании следующего выражения:

Если окажется, что t_r £ t_*, то первый коэффициент автокорреляции временного ряда фактической ошибки e_t можно принять равным нулю, и в этом случае ее автокорреляционные взаимосвязи можно считать статистически несущественными.

Второй способ оценки значимости коэффициента r ₁ с точки зрения математической статистики является более строгим. При его проведении вместо выборочной оценки коэффициента автокорреляции r ₁ используется его преобразование

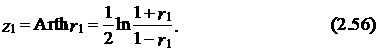
Фишер показал, что величина z ₁ распределена приблизительно по нормальному закону с нулевым средним практически при любых значениях r ₁<1 даже при не слишком большой выборке. Вследствие этого расчетное значение критерия Стьюдента, используемое при проверке гипотезы о независимости рядов е_t и е_{t +1}, может быть определено по формуле 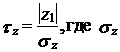– среднеквадратическая ошибка переменной z ₁. В практических расчетах ее можно заменить оценкой, полученной из выражения (2.55).