Отрицательная биномиальная модель

Как уже отмечалось, в пуассоновской модели предполагается, что математическое ожидание и дисперсия числа событий у_t равны друг другу. Это свойство существенно ограничивает ее применение, поскольку реальные процессы им не обладают. Вследствие этого в эконометрических исследованиях обычно рассматриваются некоторые модификации пуассоновской модели, в которых свойство (10.122) не выполняется. Например, в условное математическое ожидание (выражение (10.119)) вводится ненаблюдаемое воздействие, которое предполагается случайным:

m_t ×= l_t × u_t = ,

где m_t – условное (по воздействию u_t) математическое ожидание переменной y_t; u_t = .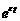

Согласно выражению (10.127) распределение у_t, обусловленное факторами x _t и ошибкой u_t, остается пуассоновским. Его плотность, определяемая набором вероятностей Р (y_t = j | x _t, u_t), имеет следующий вид:

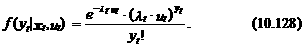
Из выражения (10.128) следует, что вероятность числа событий y_t = j при условии x _t, u_t является случайной величиной, зависящей от ошибки u_t, M [ Р (y_t = j | x _t, u_t)]= 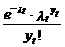= f (y_t | x _t). В этом случае функция плотности “обычного” пуассоновского закона имеет вид математического ожидания функции (10.128):

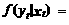^ò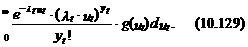

где g (u_t) – функция плотности распределения ошибки u_t.

Вид функции g (u_t) определяет и характер распределения у_t | x _t. В теории с целью упрощения математических выкладок в качестве g (u_t) обычно рассматривают гамма-распределение, т. е.

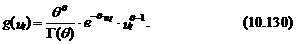
С учетом (10.130) выражение математического ожидания функции плотности примет следующий вид:

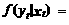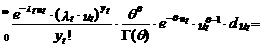
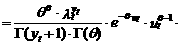^ò

^ò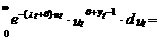

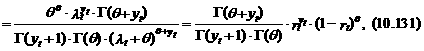
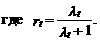
Заметим, что выражение (10.131) является одной из форм представления плотности отрицательного биномиального распределения. Это распределение имеет условное математическое ожидание по x _t, равное l_t, и условную дисперсию – l_t ×(1+(1/ q)× l_t). Таким образом, действительно снимается главное ограничение пуассоновской модели – условие равенства математического ожидания и дисперсии числа событий.