Двумерные и многомерные probit-модели

Probit - модели могут быть могут быть использованы для определения вероятностей сложных событий, выражаемых в виде комбинаций некоторых наборов простых событий, каждое из которых имеет два альтернативных варианта, например, переезд (непереезд) на новое место жительства и аренда (покупка) жилья и т. п. В этом случае данные вероятности могут быть определены как вероятности выбора в рамках многомерных альтернативных вариантов.

Для каждого индивидуума t (t =1,2,..., Т) модель, определяющая вероятности двух событий, может быть представлена в виде следующей системы:

y _{1 t} ^*= a ¢₁ x _{1 t} + e _{1 t} , если y _{1 t} =1, то y ₁^*>0, если y ₁=0, то y ₁^*£0;

y _{2 t} ^*= a ¢₂ x _{2 t} + e _{2 t} ,если y _{2 t} =1, то y ₂^*>0, если y ₂=0, то y ₂^*£0. (10.72)

Латентные переменные y _{1 t} ^* и y _{2 t} ^* модели (10.72) могут интерпретироваться в терминах выгоды, получаемой в зависимости от принятого решения соответственно в первом и во втором случаях; х _{1 t} и х _{2 t} – векторы значений независимых факторов, соответствующих сделанному выбору; e _{1 t} и e _{2 t} – ошибки соответственно первого и второго уравнений; r – коэффициент ковариации ошибок e ₁ и e ₂.

Закон совместного распределения ошибок модели e ₁ и e ₂ в общем случае характеризуется следующими параметрами:

M [ e ₁]= M [ e ₂]=0;

D [ e ₁]= D [ e ₂]=1^*;

Cov[ e ₁, e ₂]= r,

Согласно модели (10.72) возможны следующие комбинации решений:

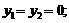
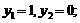
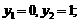
Наблюдаемые комбинации образуют массив зависимых переменных модели (10.72).

В системе (10.72) допускается, что события являются зависимыми между собой, что означает существование ненулевой ковариационной связи между ошибками e ₁ и e ₂. Например, возможность приобретения жилья на новом месте может способствовать принятию решения о переезде или, наоборот, переезд обусловливает необходимость аренды жилья.

Для определения функции закона распределения введем следующие обозначения: q _{1 t} =2 y _{1 t} –1 и q _{2 t} =2 y _{2 t} –1^*. Тогда q_jt =1, если у_jt =1, и q_jt =–1, если у_jt =0, для j =1,2. Введем также в рассмотрение следующие переменные:

z_jt = a ¢ _j x _jt и w_jt = q_jt × z_jt, j =1,2

и

r_{t *}= q _{1 t} × q _{2 t} × r.

Вероятность того, что зависимые переменные Y ₁ и Y ₂ системы (10.72) для конкретного индивидуума принимают соответственно значения y _{1 t} и y _{2 t} , при, например, нормальном виде закона их совместного распределения рассчитывается как

P (Y ₁= y _{1 t} , Y ₂= y _{2 t} )=F₂(w _{1 t} , w _{2 t} , r_t*), (10.74)

где F₂(.) – функция нормального закона совместного распределения случайных переменных Y ₁ и Y ₂, имеющая следующий вид:

F₂(w _{1 t} , w _{2 t} , r_t*)=ò ò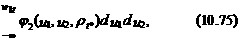

где u ₁ и u ₂ – переменные интегрирования и плотность этого распределения имеет следующий вид:

Для определения маржинальных эффектов в модели (10.72) введем в рассмотрение вектор х _t, являющийся объединением векторов х _{1 t} и х _{2 t} ^* , и вектор коэффициентов g ₁, такие что a ₁¢ х _{1 t} = g ₁¢ х _t. Вектор g ₁ составлен из элементов вектора коэффициентов a ₁ и нулей, стоящих на позициях, которые соответствуют переменным второго уравнения. Аналогичным образом введем вектор коэффициентов g ₂: a ₂¢ х _{2 t} = g ₂¢ х _t. Тогда вероятность того, что значения y ₁ и y ₂одновременно будут равны единице определяется следующим выражением:

P (y ₁=1, y ₂=1)=F₂[ g ₁¢× x _t, g ₂¢× x _t, r_{t *}]. (10.77).

Маржинальные эффекты независимых факторов x _t для P (y ₁=1, y ₂=1) могут быть определены согласно следующему выражению:

g _{1 t} × g ₁+ g _{2 t} × g ₂,

где

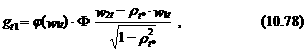
Для получения g_{t 2} индексы 1 и 2 в выражении (10.78) нужно поменять местами^*.

Математические ожидания зависимых переменных y_j, j =1,2 для конкретных наборов независимых переменных х _t в соответствии с выражением (10.50) определяются как

M [ y_j | x _t ]= F(g _j ¢× x _t), j =1,2. (10.79)

Для модели (10.72) можно также определить условные математические ожидания переменных y _{1 t} и y _{2 t} .

Например, математическое ожидание зависимой переменной первого уравнения при условии, что y ₂=1, определяется согласно формуле условной вероятности следующим образом:

M [ y ₁| y ₂=1, x _t ]= P [ y ₁=1| y ₂=1, x _t ]=

=P [ y ₁=1, y ₂=1| x _t ]/ P [ y ₂=1| x _t ]=

=F₂(g ₁¢× x _t, g ₂¢× x _t, r _{t *})/F(g ₂¢× x _t) (10.80)

Аналогично определяется математическое ожидание зависимой переменной второго уравнения при условии, что y ₁=1.

Маржинальные эффекты факторов x _t для функции типа (10.80) рассчитываются как

¶ M [ y ₁| y ₂=1, x _t ]/¶ x _t =

=[1/F(g ₂¢× x _t)]×[ g_{t 1}× g ₁+(g_{t 2}–F₂×(j (g ₂¢× x)/ F(g ₂¢× x _t))× g ₂]. (10.81)

Аналогичным образом могут быть построены модели с тремя и более зависимыми переменными, с учетом того, что функционал F должен выражать их совместное распределение.