Гнездовые logit-модели (nested logit-models)

Как было отмечено, в условной logit -модели ошибки обычно предполагаются гомоскедастичными. Для практики это предположение часто является слишком строгим. Например, в случае выбора одного из трех торговых центров при условии, что количество магазинов в первом из них вдвое больше, чем во втором (K ₁=2 K ₂), а расстояние до первого вдвое больше, чем до второго (R_{t 1}=2 R_{t 2}), дисперсии ошибок e ₁ и e ₂ эконометрической модели, связывающей данные выбора первого и второго торгового центра с влияющими на этот выбор факторами (см. выражение (10.96)), определяются следующим образом:

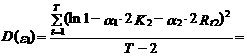
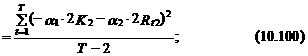
где T – число наблюдений.

Если 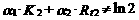, то D (e ₁)¹ D (e ₂), т. е. ошибки e_j гетероскедастичны.

Один из способов ослабить предположение о гомоскедастичности ошибок в условной logit -модели связан с изменением процедуры выбора альтернативных вариантов. В этом случае варианты разделяются на непересекающиеся группы таким образом, что внутри группы дисперсии ошибок e_tj уравнения (10.84) являются одинаковыми, а дисперсии ошибок разных групп между собой различаются.

Предположим, что J вариантов могут быть разбиты на L групп, и общий набор вариантов представляется как [1,..., J ]=[(1|1,..., J 1|1),..., (1| L,..., JL | L)], где j | l – j вариант в группе l, Jl – номер последнего варианта в группе l. Используется следующая логика выбора окончательного решения. Сначала выбирается одна из L групп, затем осуществляется выбор варианта в рамках группы. Этот процесс имеет древовидную структуру, которая для двух групп и 5 вариантов может выглядеть следующим образом:

Выбор

Группа₁ Группа₂

1|1 2|1 1|2 2|23|2

Пусть х _{j | l} – вектор независимых переменных, влияющих на выбор варианта внутри группы, а z _l – вектор независимых переменных, влияющих на выбор группы.

Если бы для описания процедуры выбора использовалась условная logit -модель (10.92), то предполагалось бы, что выбор варианта j и выбор группы l не зависят друг от друга.

При условии независимости выбора группы и варианта внутри группы вероятность выбора конкретного варианта определялась бы следующим выражением:

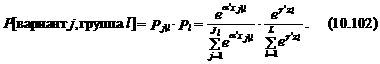
где a и g – вектора параметров.

Для гнездовой logit -модели безусловную вероятность выбора j -го варианта и l -й группы можно представить как произведение условной вероятности выбора j -го варианта при условии, что была выбрана l -я группа, и безусловной вероятности выбора l -й группы.

Заметим, что поскольку внутри группы ошибки гомоскедастичны, то условную вероятность выбора j -го варианта при условии выбора l -й группы, можно определить с использованием выражения (10.92) как

Специфика гнездовой logit -модели, ее отличие от условной logit -модели, состоит в подходе к определению вероятности выбора l -й группы. Для того чтобы раскрыть эту специфику, введем переменную I_l, характеризующую “ценность” l -й группы:

В гнездовой logit -модели “ценность” l -й группы рассматривается как дополнительный фактор, влияющий на выбор этой группы, т. е. вероятность выбора l -й группы определяется следующим образом:

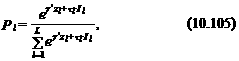
где t_l – параметр, который и отличает гнездовую logit -модель от условной logit -модели. В последней он принимает значение 1. Поэтому вероятность выбора l -й группы в условной logit -модели определяется как

В гнездовой logit -модели значение параметра t_l оценивается вместе с параметрами g.

В целом, оценивание безусловной вероятности выбора j -го варианта внутри l -й группы в рамках гнездовой модели осуществляется следующим образом:

1. Вектор параметров a оценивается с использованием условной logit -модели типа (10.92), описывающей выбор j -го варианта в зависимости от факторов х _{j | l} . После оценки параметров a по формуле (10.103) определяется ценность l -й группы, т. е. I_l.

2. Вектор параметров g и параметр t_l также оцениваются с использованием условной logit -модели типа (10.92), которая описывает выбор l -й группы в зависимости от факторов z _l и I_l.

3. По формулам (10.103), (10.105) оцениваются вероятности P_{j | l} и P_l. Безусловная вероятность выбора j -го варианта внутри l -й группы определяется как произведение P_{j | l} и P_l.

Качество оценок, получаемых на основе гнездовой logit -модели, во многом определяется правильностью построения дерева альтернативных вариантов. Отметим, что на практике достаточно трудно оценить, соответствует ли выбранная структура такого дерева исходным условиям модели, состоящих в постулировании определенных допущений относительно дисперсий ошибок (постоянство дисперсий ошибок внутри группы и различие дисперсий в разных группах).

Как это было показано ранее, модификации logit -моделей могут формироваться в зависимости от состава учитываемых в них факторов. В частности, мультиномиальная logit-модель в отличие от рассмотренных выше модификаций учитывает, что на выбор индивидуума t влияют только его характеристики. Примером мультиномиальной logit -модели является модель выбора сферы деятельности (Schmidt and Strauss, 1975). Допустим, что имеется информация: а) относительно возможной сферы деятельности человека: (0) – “прислуга”, (1) – “синий воротничок”, (2) – “ремесленник”, (3) – “белый воротничок”, (4) – “руководитель”; б) относительно характеристик индивидуума (факторов): образование, опыт работы в данной области, пол.

Предположим, что значения зависимой переменной y_t и независимых факторов w _t, связаны следующим образом:

y_t = a _j ¢× w _t + e_tj, (10.107)

где y_t наблюдаемые значения зависимой переменной (т. е. 0, 1,..., J); w _t – вектор факторов, содержащий характеристики индивидуума t; a _j – вектор параметров, характеризующих влияние факторов w _t на выбор конкретного варианта j, e_tj – ошибка модели.

Предположим также, что ошибки e_tj, j =1,..., J независимы и распределены по закону Вейбулла, т. е.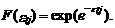

Тогда вероятность выбора t -м индивидуумом j -го варианта может быть представлена в следующем виде (см. выражения (10.89)–(10.91)):

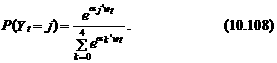
Заметим, что в приведенном примере рассматривается нулевая альтернатива. Это позволяет сократить объем вычислений, поскольку на практике a ₀ не оценивают, а принимают равным нулевому вектору. Тогда согласно выражению (10.108) вероятности выбора t -м индивидуумом варианта j, j =0,1,..., J– 1;определяются согласно следующим формулам:

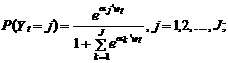
Из выражений (10.109) следует, что логарифм отношения вероятностей выбора j -й и 0-го варианта равен

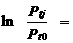a _j ¢× w _t ×, (10.110)

а логарифм отношения вероятностей выбора j -го и k -го вариантов –

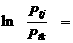w _t ¢×(a _j – a _k). (10.111)

Заметим, что, если предположение о независимости ошибок e_tj не выполняется, то соотношения между вероятностями нуждаются в определенной корректировке.

Модели с упорядоченными альтернативными вариантами.

Варианты в моделях множественного выбора могут быть естественным образом упорядочены. Примерами упорядоченных вариантов являются:

1. Рейтинги ценных бумаг.

2. Результаты дегустации.

3. Опросы общественного мнения.

4. Уровни сложности работ.

5. Типы страховых полисов, выбираемых потребителем (отсутствие такового, частичное покрытие, полное покрытие).

6. Степени занятости (безработный, занят часть дня, занят полный день).

Во всех этих случаях значения зависимой переменной обычно выражают отношения предпочтения среди альтернативных вариантов. Такие отношения могут быть выражены рангами, имеющими вид упорядоченных наборов чисел: 0,1,2,... При этом наиболее предпочтительному варианту может соответствовать как нуль (в этом случае рейтинги вариантов с ростом их ранга уменьшаются), так и последнее число в этой последовательности J (в этом случае рейтинги альтернатив уменьшаются вместе с уменьшением их ранга).

Для анализа определения предпочтительности выбора среди упорядоченных альтернативных вариантов и оценки влияния на этот выбор различных факторов широко применяются порядковые logit - и probit -модели. В таких моделях вероятности предпочтения также, как и в биномиальной probit -модели (10.58), определяются с использованием уравнения латентной регрессии:

y_t ^*= a ¢× x _t + e_t. (10.112)

где y_t ^* – ненаблюдаемая переменная, которая по-прежнему представляет собой выгоду (полезность) выбора j -го варианта для t -го индивидуума, например, дивиденды от покупки акций с j -м рейтингом; a – вектор параметров; x _t – вектор независимых переменных, влияющих на выбор t -го индивидуума; e_t – ошибка модели.

Если значение переменной у_t ^* удовлетворяет условию у_t ^*<0, то предполагается, что индивидуум с характеристиками x _t, выбирает нулевой альтернативный вариант. Аналогично, если выполняется условие 0< y ^*£ m ₁, то выбирает первый вариант и т. д. Эту логику выбора можно представить в виде следующей системы:

если y_t ^*£0, то y_t =0;

если 0< y_t ^*£ m ₁, то y_t =1;

если m ₁< y_t ^*£ m ₂, то y_t =2;

................

если m_{J –1}£ y_t ^*, то y_t = J. (10.113)

где m_j (j =1,2,..., J –1) – неизвестные параметры, которые подлежат оценке, как и параметры a (и оцениваются теми же методами). Границы m ₁,..., m_{J– 1} можно интерпретировать как один из вариантов цензурирования.

Предположим, что ошибки e_t нормально распределены, e ~ N [0,1]^*. С учетом этого набор вероятностей появления j -й наблюдаемой переменной (j -го ответа) определяется следующими выражениями:

P (y_t =0)=F(– a ¢× x _t);

P (y_t =1)=F(m ₁– a ¢× x _t)–F(– a ¢× x _t);

P (y_t =2)= F(m ₂– a ¢× x _t)–F(m ₁– a ¢× x _t);

.......................... (10.114)

P (y_t = J)=1–F(m_{J –1}– a ¢× x _t).

где F(.) – функция закона стандартного нормального распределения.

Из выражений (10.114) следует, что эти вероятности Р (y_t = j), j =0,..., J будут положительными, если выполняется следующее условие:

0< m ₁< m ₂<... < m_{J –1}. (10.115)

На рис. 10.4 показано распределение вероятностей выбора конкретных альтернатив.

Рассмотрим особенности определения маржинальных эффектов факторов х _t, которые будут характеризовать изменение вероятности выбора j -го альтернативного варианта при изменении одного из независимых факторов на 1 единицу. Допустим, имеется три варианта (этот случай предполагает только один параметр положения m). В соответствии с выражением (10.114) вероятности выбора каждого из вариантов определяются как

P (y_t =0)=F(– a ¢× x _t);

P (y_t =1)= F(m – a ¢× x _t)–F(– a ¢× x _t);

P (y_t =2)=1–F(m – a ¢× x _t) (10.116)

et

a ¢ xt

m 3 –a ¢ xt

m 1 –a ¢ xt

yt =3

yt =0

m 2 –a ¢ xta ¢ x a ¢ x

yt =4

yt =2

yt =1

f (et)

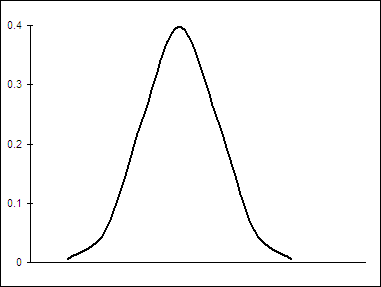
Рис.10.4. Вероятности в упорядоченной probit-модели.

Тогда маржинальные эффекты факторов определяются согласно следующему выражению:

¶ P [ y_t =0]/¶ x _t =– j (a ¢× x _t)× a;

¶ P [ y_t =1]/¶ x _t =[ j (– a ¢× x _t)– j (m – a ¢× x _t)]× a;

¶ P [ y_t =2]/¶ x _t = j (m – a ¢× x _t)× a. (10.117)

где j (.) – функция плотности распределения стандартной нормальной переменной.

На рис. 10.5 сплошной линией изображено распределение y_t в зависимости от ошибки e_t. Рисунок характеризует маржинальный эффект при увеличении одного из факторов х_it (i =1,2,..., n) при неизменных a и m. Этот эффект эквивалентен смещению графика распределения вправо, что показано пунктирной линией.

yt =2

yt =1

yt =0

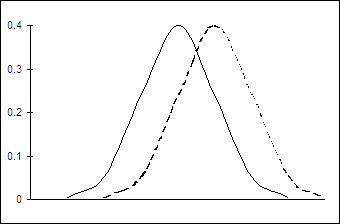
Рис.10.5. Влияние изменения хt на оцененные вероятности.

Согласно первому выражению в (10.117) изменение вероятности выбора 0-го варианта зависит от коэффициента при факторе х_i. Если коэффициент a_i положителен (для данного набора х _t), то вероятность P [ y_t =0] должна снизиться (производная ¶ P [ y_t =0]/¶ х_it имеет знак, противоположный знаку a_i). Соответственно, если коэффициент a_i отрицателен, то вероятность P [ y_t =0] должна повыситься.

Согласно третьему выражению в (10.117) направление изменения вероятности P [ y_t =2] при увеличении фактора х_i, также определяется знаком коэффициента a_i: но в данном случае при положительном a_i вероятность увеличивается, при отрицательном a_i – уменьшается.

Заметим, что согласно второму выражению в (10.117) изменение вероятности P [ y_t =1] зависит не только от знака a_i, но и от знака, который будет иметь разность двух плотностей [ j (– a ¢× x _t)– j (m – a ¢× x _t)]. Если эти знаки совпадают, что вероятность P [ y_t =1] увеличивается с увеличением х_it, если не совпадают, то она уменьшается.