 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Модели бинарного выбора
|
|
Модели бинарного выбора широко используются в экономических и социальных исследованиях, особенно в экономике труда, при проведении анализа на микро-уровне. Покажем их специфические свойства на примере модели трудовой активности населения, исходные предпосылки которой состоят в следующем. Индивидуум в определенный период времени может работать или искать работу (y =1) или не делать этого (y =0). Предположим, что состояние “работать” или “не работать” определяется набором факторов (возраст, семейное положение, образование, опыт работы и т. д.), и соответствующие вероятности можно представить в следующем виде:
P (y =1)= F (a ¢ x);
P (y =0)=1– F (a ¢ x). (10.41)
Вектор коэффициентов a отражает влияние факторов, например, характеризующих положение индивидуума в обществе, на рассматриваемую вероятность.
Одной из основных проблем при построении моделей бинарного выбора является обоснование функционала F (a ¢ x). Например, предположим, как и в случае “классических” эконометрических моделей, что вероятности соответствующих событий могут быть представлены в виде линейной функции от значений рассматриваемых факторов:
F (a ¢ x)= a ¢ x = a 0+ a 1 x 1+...+ anxn, (10.42)
где a 0, a 1,..., an – параметры модели; x 1,..., xn – значения независимых факторов.
Тогда, приняв 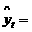 M [ yt | x t ]= F (a ¢ x t), соответствующую эконометрическую модель можно представить в следующем виде:
M [ yt | x t ]= F (a ¢ x t), соответствующую эконометрическую модель можно представить в следующем виде:
yt = M [ yt | x t ]+(yt – M [ yt | x t ])= a ¢ x t + e t. (10.43)
где M [ yt | x t ]= 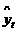 – условное математическое ожидание переменной yt при условии, что вектор независимых переменных равен x t.
– условное математическое ожидание переменной yt при условии, что вектор независимых переменных равен x t.
Линейная форма модели представляет определенное удобство для раскрытия содержания, входящих в нее слагаемых. Прежде всего заметим, что между их значениями выполняется следующие соотношения (см. табл. 10.1).
Таблица 10.1
| уt | P (уt =...)= 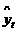
| et |
| a ¢ xt | 1– a ¢ xt (с вероятностью a ¢ xt) | |
| a ¢ xt | – a ¢ xt (с вероятностью 1– a ¢ xt) |
Из табл. 10.1. следует, что ошибки et модели (10.43) имеют следующие характеристики:
M [ et ]= a ¢ x t (1– a ¢ x t)+ (1– a ¢ x t)(– a ¢ x t)=0;
D [ et | x t ]= a ¢ x t (1– a ¢ x t)2+(1– a ¢ x t)(– a ¢ x t) 2= a ¢ x t (1– a ¢ x t)(1– a ¢ x t + a ¢ x t)=
= a ¢ x t (1– a ¢ x t). (10.44)
где D [ et | x t ] – условная дисперсия ошибки et при условии, что вектор независимых переменных равен x t.
Рассмотрим в качестве критерия выбора оценок параметров модели (10.43) минимум суммы дисперсий ее ошибок et:
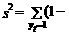 a ¢ x t)2+
a ¢ x t)2+ 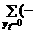 a ¢ x t) 2=
a ¢ x t) 2= 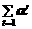 x t (1– a ¢ x t)2+
x t (1– a ¢ x t)2+ 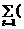 1– a ¢ x t)(– a ¢ x t)2=
1– a ¢ x t)(– a ¢ x t)2=
= 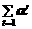 x t (1– a ¢ x t)=
x t (1– a ¢ x t)= 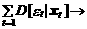 min. (10.45)
min. (10.45)
Используя МНК для оценки параметров модели (10.43) при критерии (10.45), получим следующую систему “нормальных” уравнений, относительно неизвестных оценок а 0, а 1,..., аn:
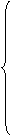
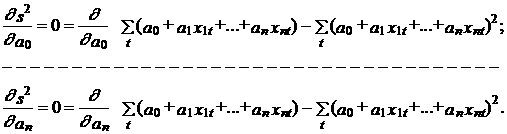
Выполнив дифференцирование с учетом попарной независимости коэффициентов между собой и со значениями факторов хit, i =1,2,..., T, эту систему можно представить в следующем виде:
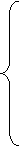
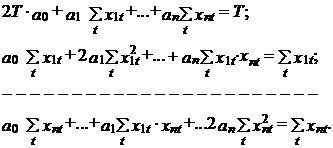
В свою очередь, последняя система может быть представлена в векторно-матричном виде следующим образом:

| 
| ||||

| |||||
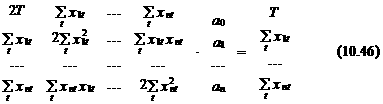
или в компактной форме записи как
X × a = z, (10.47)
 где матрица
где матрица 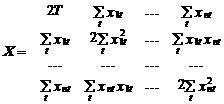 и вектор-столбец
и вектор-столбец 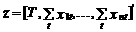 .
.
Из выражения (10.47) непосредственно вытекает, что неизвестные оценки параметров бинарной модели линейного типа могут быть получены на основании следующего выражения:
a = X –1× z, (10.47)
Однако линейная интерпретация (10.42) закона распределения вероятностей достаточно “неудобна” по своим “эконометрическим следствиям”.
Во-первых, заметим, что из выражения (10.44) вытекает, что ошибка e гетероскедастична, поскольку дисперсия ошибки зависит от вектора x. В таких условиях оценки параметров a модели (10.43), полученные на основе выражения (10.48), являются неэффективными. Для получения эффективных оценок ее параметров, необходимо использовать обобщенный МНК.
Во-вторых, любой метод оценки параметров линейных моделей бинарного выбора не дает гарантий, что результат произведения a ¢ x может принимать значения только на интервале [0, 1]. С учетом выражения (10.44) несложно заметить, что при отрицательных значениях этого произведениях и значениях больших единицы будет иметь место и другой абсурдный результат – отрицательная дисперсия остатков. Это обстоятельство существенно ограничивает область применения линейной модели бинарного выбора. На практике она используется только для предварительной обработки данных и для сопоставления с результатами, полученными более тонкими методами.
Из приведенных рассуждений вытекает, что модель бинарного выбора должна удовлетворять двум условиям:
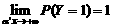
и

где a ¢ x ®+¥ – область значений x, при которых P (y =1)=1, а a ¢ x ®–¥ – область значений x, при которых P (y =1)=0.
При этом между значениями составных частей регрессионного уравнения должно выполняться следующее соответствие (см. табл. 10.2).
Таблица 10.2
| уt | P (уt =...)= 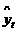
| et |
| F (a ¢ xt) | 1– F (a ¢ xt) | |
| 1– F (a ¢ xt) | –(1– F (a ¢ xt)) |
Условиям (10.49) отвечает, например, функция F (a ¢ x), близкая к закону нормального распределения, график которой представлен на рис. 10.2. Ее использование позволяет снять рассмотренные выше ограничения моделей бинарного выбора. Модели с функционалом, обладающим свойством “нормального закона“, в литературе получили название probit -моделей:
P (Y =1)=ò 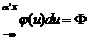 (a ¢ x). (10.50)
(a ¢ x). (10.50)
где Ф(.) – функция стандартного нормального распределения, зависящая от значений факторов x и параметров a, j (u)– функция плотности распределения стандартной нормальной переменной u.
В предположении о независимости и гомоскедастичности ошибок et функцию j (u) можем записать в следующем виде:

|
j (a ¢ x t)= 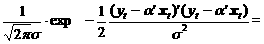

|
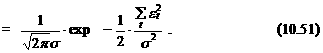
Заметим, что s 2в выражении (10.51) является неизвестным параметром, который должен быть оценен, как и вектор параметров a.
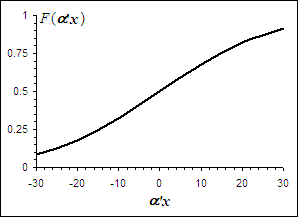
Рис.10.2 График функции закона распределения, близкого к нормальному.
Из выражения (10.51) вытекает, что между значениями независимой переменной уt и j (a ¢ x t) выполняется следующее соотношение (см. табл. 10.3).
Таблица 10.3
| уt | j (a ¢ xt) |
      1 1
| 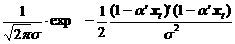
|
      0 0
| 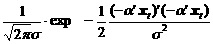
|
Не менее широко в моделях бинарного выбора используется и логистическое распределение:
P (Y =1)= 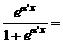 L(a ¢ x). (10.52)
L(a ¢ x). (10.52)
где L(.) представляет собой интегральную функцию логистического распределения.
Модели, построенные на его основе, называются logit -моделями. Несложно заметить, что в данном случае между составными частями регрессионного уравнения выполняется следующее соотношение (см. табл. 10.4).
Таблица 10.4
| уt | P (уt =...)= 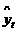
| et |
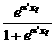
| 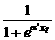
| |
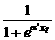
| 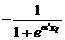
|
Вопрос о том, какое из вышеназванных распределений более подходит для практических исследований, остается открытым. На участке a ¢ x Î[–1,2; 1,2] оба они ведут себя практически одинаково. Однако вне этого участка, т. е. на хвостах распределения, значения функционалов Ф(a ¢ x) и L(a ¢ x) имеют некоторые отличия. В частности, логистическое распределение имеет более “тяжелый хвост”, чем нормальное. Практика показывает, что при отсутствии существенного преобладания одной альтернативы над другой, а также для выборок с небольшим разбросом переменных, выводы, полученные на основе probit - и logit -моделей, как правило, совпадают.
В общем случае из выражения (10.41) для модели бинарного выбора вытекает, что условное математическое ожидание зависимой переменной при заданном наборе факторов может быть определено следующим выражением:
M [ yt | x t ]=0×[1– F (a ¢ x t)]+1× F (a ¢ x t)= F (a ¢ x t). (10.53)
Одно из направлений использования результата (10.53) в анализе рассматриваемых явлений связано с оценками так называемого маржинального эффекта факторов, входящих в модель. Маржинальный эффект фактора xit, i =1,2,..., n; t =1,2,.., T показывает изменение функции F (a ¢ x t) (характеризующей вероятность того, что у =1) при изменении фактора xit на единицу.
Маржинальные эффекты факторов x t для модели бинарного выбора оцениваются на основе следующего выражения:
¶ M [ yt | x t ]/¶ x t ={¶ F (a ¢ x t)/ ¶(a ¢ x t)}× a = f (a ¢ x t)× a, (10.54)
где f (.) – плотность безусловного распределения, соответствующая интегральному распределению F (.) и дифференцирование осуществляется по вектору x t. В частности, для нормального распределения маржинальный эффект рассчитывается по формуле
¶ M [ yt | x t ]/¶ x t = f (a ¢ x t)× a, (10.55)
где f (.) – плотность стандартного нормального распределения.
Для логистического распределения производная функции этого закона по факторам x t функция f (a ¢ x t) имеет следующий вид:
¶L[ a ¢ x t ]/¶ x t = e a ¢ x / (1+ e a ¢ x)2 =L(a ¢ x t)×[1–L(a ¢ x t)]. (10.56)
Соответственно в logit -модели маржинальные эффекты определяются как
¶ M [ yt | x t ]/¶ x t =L(a ¢ x t)×[1–L(a ¢ x t)]× a, (10.57)
Из выражений (10.54)–(10.57) вытекает, что величина маржинального эффекта для probit - и logit -моделей зависит от значений независимых факторов x. В связи с этим полезно будет определить так называемый “средний маржинальный эффект” в области существования значений независимых факторов.
На практике возможны два подхода к его оценке. Первый основан на усреднении значений независимых факторов, т. е. сначала рассчитываются выборочные средние всех факторов 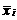 , i =1,2,..., п, а затем для оценки среднего эффекта определяется f (a ¢
, i =1,2,..., п, а затем для оценки среднего эффекта определяется f (a ¢ 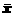 )× a. В соответствии со вторым подходом маржинальные эффекты оцениваются для каждого наблюдения, затем по полученным оценкам этих индивидуальных маржинальных эффектов определяется его среднее значение.
)× a. В соответствии со вторым подходом маржинальные эффекты оцениваются для каждого наблюдения, затем по полученным оценкам этих индивидуальных маржинальных эффектов определяется его среднее значение.
Поскольку функция (10.51) у рассматриваемых моделей непрерывна, то в соответствии с теоремой Слуцкого* на больших выборках оба подхода будут давать один и тот же набор средних маржинальных эффектов. Но это неверно для малых выборок. Практика показывает, что в этом случае лучшие результаты дает второй подход, основанный на усреднение индивидуальных маржинальных эффектов.
Заметим, что средний маржинальный эффект бинарной независимой переменной (например, с) можно определить как следующую разность: P [ y =1| 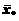 , с =1]– P [ y =1|
, с =1]– P [ y =1| 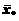 , с =0], где
, с =0], где 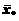 – вектор выборочных средних значений остальных независимых переменных х.
– вектор выборочных средних значений остальных независимых переменных х.
Обратим внимание на то, что результаты моделей бинарного выбора могут иметь разнообразное содержание. В частности, их можно проинтерпретировать в терминах выгоды или ущерба. Рассмотрим такую интерпретацию на примере модели крупной покупки. Исходными данными (наблюдаемыми переменными) в этом случае являются сведения о покупке (1 – покупка сделана, 0 – в противном случае) и факторы, характеризующие субъекта, потребителя (доход, пол, возраст и т. д.). Далее предполагается, что покупка имеет место, если она приносит выгоду потребителю, и покупка отсутствует, если такой выгоды нет, и даже возможен “ущерб” (например, покупка бесполезна).
Ненаблюдаемую (латентную) выгоду, получаемую t -м потребителем от покупки, будем моделировать как переменную yt *, определяемую следующим выражением:
yt *= a ¢ x t + et, (10.58)
где a ¢ x t в данном случае называется индексной функцией (index funktion); et – ошибка модели, в отношении которой делается предположение, что она имеет стандартное нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.
Вероятность получения t -м потребителем выгоды от покупки может быть определена следующим образом:
P (yt *>0)= P (a ¢ x t + et >0)= P (et >– a ¢ x t). (10.59)
Если распределение симметрично (каковыми являются нормальное и логистическое), то выражение (10.59), можно представить в следующем виде:
P (yt *>0)= P (e < a ¢ x t)= F (a ¢ x t). (10.60)
В качестве примера модели типа (10.58)–(10.60) рассмотрим модель миграции, разработанную Нейкостином и Циммером (Nakosteen, Zimmer, 1980). В ее основе лежит предположение о том, что индивидуум принимает решение о переезде, если это приносит ему определенную выгоду, которая оценивается на основе сопоставления доходов в настоящем и “новом” месте его проживания, затрат на переезд.
Доход yp *, который индивидуум может получить в данной местности настоящего проживания за год, определяется как
yp *= a ¢ x p + ep, (10.61)
где a – вектор значений параметров; x p – вектор независимых переменных, характеризующих индивидуума, например, возраст, образование, опыт работы, и т. д.; ep – ошибка модели.
Если индивидуум переезжает на новое место, то его доход ym * будет определяться согласно следующему выражению:
ym *= b ¢ x m + em, (10.62)
где b – вектор значений параметров; x m – вектор независимых переменных, состав которых может как совпадать, так и не совпадать с составом компонент вектора x p (включать, например, возможность получения более престижной должности); em – ошибка модели.
Переезд связан с определенными затратами C *, которые могут быть связаны линейной зависимостью со статусом индивидуума (предприниматель, наемный работник, семейный или несемейный и т. д.):
C *= g ¢ z + u, (10.63)
где z – вектор независимых переменных, характеризующих статус индивидуума; u – ошибка модели.
С учетом вышеперечисленного выгода от переезда может быть представлена в следующем виде:
N *= ym *– yp *– C *= b ¢ x m – a ¢ x p – g ¢ z +(em – ep – u)= d ¢ w + e, (10.64)
где w – вектор независимых переменных, характеризующих индивидуума, условия его жизнедеятельности в местах его жительства и т. п., которые влияют на уровень доходов и затраты на переезд; e = em – ep – u – ошибка модели.
В целом, вероятность переезда P (N =1) определяется следующим образом:
P (N *>0)= P (d ¢ w + e >0)= P (e >– d ¢ w). (10.65)
Выражение (10.65) полностью соответствует выражению (10.59).
Альтернативную интерпретацию данных об индивидуальных предпочтениях дает модель случайной полезности (random utility model). Согласно этой интерпретации латентные (ненаблюдаемые) переменные предыдущей задачи, т. е. ym и yp, представляют собой полезности для индивидуума двух выборов (переезжать или не переезжать). В другом примере латентные переменные могут характеризовать полезность аренды дома и полезность владения домом. Статистика индивидуальных выборов, т. е. значения yt =1 и yt =0, дают возможность оценить, какая из альтернатив имеет большую полезность при соответствующих наборах факторов, но при этом величина полезности остается неопределенной. Обозначим полезность аренды дома через Ua, а полезность владения домом – через Ub. Наблюдаемый индикатор yt равняется 1, если Ua > Ub, и равняется 0, если Ua £ Ub.
Общая постановка модели случайной полезности выглядит следующим образом:
Ua = a ¢ a x + ea;
Ub = a ¢ b x + eb. (10.63)
где a a и a b – различающиеся между собой вектора параметров модели; индексы а и b характеризуют варианты выбора.
Тогда, вероятность выбора варианта а (наблюдаемая переменная y принимает значение 1) определяется по следующей формуле:
P (y =1| x)= P [ Ua > Ub ]= P [(a ¢ a x + ea – a ¢ b x – eb | x ]=
= P [(a a – a b)¢ x + ea – eb >0| x ]= P [ a ¢ x + e >0| x ]. (10.64)
На практике по известным значениям наблюдаемой переменной yt оценивается вектор a = a a – a b.
Рассмотренные выше модели использовали, так называемые индивидуальные данные. Каждое наблюдение содержало набор значений [ yt, x t ], характеризующих реальный выбор отдельного индивидуума и соответствующий вектор независимых факторов. Вместе с тем, часто при построении моделей бинарного выбора используются групповые данные, которые выражают результаты подсчетов или пропорций. Обозначим через kt количество индивидуумов, имеющих одинаковые значения, характеризующих их признаков (т. е. одинаковый вектор x t). Индекс t в этом случае выражает различные вектора признаков x t и соответствующие количества индивидуумов kt, обладающих ими. Пусть наблюдаемая зависимая переменная Nt выражает долю индивидуумов, у которых yt =1, в общем числе индивидуумов kt. С учетом этого информация для фиксированного индекса t выглядит как [ kt, Nt, x t ], t =1,..., T. Для сгруппированных таким образом данных представим зависимость доли Nt от факторов-признаков, характеризующих индивидуумов t -й группы, в следующем виде:
Nt = F (a ¢ x t)+ et = pt + et,
M [ et ]=0;
D [ et ]= pt ×(1– pt)/ kt. (10.68)
где в качестве функции F (a ¢ x t) обычно используются функции законов нормального и логистического распределений; pt – оценка доли Nt; et – ошибка модели.
В заключение раздела, посвященного рассмотрению моделей бинарного выбора, объясним происхождение терминов logit и probit. Из выражения (10.68) следует, что дисперсия ошибки e гетероскедастична. Поскольку функция F (a ¢ x t) предполагается нелинейной, то для оценки параметров следовало бы применить нелинейный МНК с весами, однако можно предложить менее громоздкий подход к решению данной задачи. Для этого обозначим через F (Nt) значение интегральной функции закона распределения в точке Nt. Тогда можно показать, что обратное значение этой функции F –1(Nt) допускает следующее представление*:
F –1(Nt)» a ¢ x t + et / f (pt)
или
F –1(Nt)= zt» a ¢ x t + ut, (10.66)
где f (pt)– значение функции плотности, соответствующей интегральной функции закона распределения F (.), в точке pt: ut = et / f (pt) – ошибка, обладающая следующими характеристиками:
M [ ut ]=0;
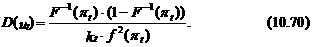
Если F (a ¢ x t) является логистической функцией, т. е.
pt =exp(a ¢ x t)/[1+ exp(a ¢ x t)],
то несложно показать, что
F –1(pt)=ln[ pt /(1– pt)]= a ¢ x t. (10.71)
Функция типа (10.71) в научной литературе получила название logit - pt. В связи с этим модели бинарного выбора, в основе которых лежит логистическое распределение, обычно называют logit -модели.
Для нормального распределения обратная функция Ф–1(pt) называется нормитом - pt. Функция Ф–1(pt) может принимать отрицательные значения, обычно не превышающие –5. Чтобы избежать работы с отрицательными числами к значению функции на практике добавляется число 5. Функция (нормит - pt +5) получила название probit - pt. Поэтому модели бинарного выбора, основанные на нормальном распределении, называются probit - модели.
Дата публикования: 2014-10-25; Прочитано: 1886 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
