Основные уравнения теории упругости

Как известно, задача по определению напряжений (исследование напряженного состояния) деформированного тела является статически неопределимой. Для её решения необходимо рассмотреть три стороны - статическою, геометрическую и физическую. Отмеченные стороны решаемой задачи базируются на соответствующих законах деформирования сплошного твердого тела – закон равновесия, закон сплошности и физический закон. Каждый из этих законов выражает определенные зависимости между элементами деформирования тела. Они являются базисными зависимостями, т.е. такими, на которых основано все решение задачи деформирования сплошного твердого тела.

Закон равновесия выражается теми же условиями равновесия, что и в случае твердого недеформированного тела, но с тем отличием, что для деформирующего тела требуется выполнение условий равновесия каждой частицы тела, ибо для него условие равновесия в целом является необходимым но недостаточным. Деформирующееся тело имеет бесконечное число степеней свободы соответственно бесконечному числу своих перемещающихся частиц. Поэтому для деформирующегося тела, в отличие от абсолютного твердого, закон равновесия выражается не алгебраическими, а дифференциальными уравнениями для сил, отнесенных к бесконечно малой (дифференциальной) частице тела.

Закон сплошности вытекает из самой сущности модели сплошного твердого тела. Он состоит в том, что тело на всех этапах деформирования до разрушения остается монолитным, сплошным, не расчленяющемся на отдельные частицы. Математически закон сплошности выражается рядом условий о непрерывности перемещений, деформаций и их производных. Однако не стоит забывать, что, модель сплошного тела есть научная абстракция от действительности. С её применением не принимаются во внимание реальное, сложное микростроение материалов и связанные с ним неоднородности тела и микроструктурные напряжения, имеющиеся в теле помимо внешних воздействий ещё до начала процесса деформирования.

Физический закон утверждает существование функциональной связи между деформациями и напряжениями, т.е. величинами, разными по своей физической сущности. Это отличает данный закон от двух предыдущих. Получение аналитического выражения физического закона, т.е. конкретной функциональной зависимостями между напряжениями и деформациями, осуществляется для каждого конкретного материала на основе соответствующих экспериментальных данных. Это функциональная зависимость может быть линейной и нелинейной. В линейной теории упругости предлагается, что материал подчиняется линейному закону, при котором напряжения и деформации находятся в линейной зависимости.

Только с применением физического закона начинается отражение конкретных («индивидуальных») механических свойств материала. В отличие от него законы равновесия и сплошности относятся ко всем материалам, независимо от их механических свойств и стадии напряженного состояния.

Статические уравнение (Навье)

Рассмотрим частицу тела в форме элементарного параллелепипеда с размерами ребер dx, dy, dz. Координаты его вершины А (x,y,z) (рис. 7) определяют положение параллелепипеда. Всем напряжениям, возникающим по его граням, задаем положительные направление. Причем все компоненты тензора напряжений 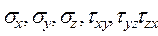рассматриваются как непрерывные функции координат x,y,z, т.е. 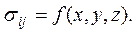Составляющие удельной объемной силы (объемной силы, приходящейся на единицу объема) x,y,z, параллельные осям x,y,z.

Для параллелепипеда как для пространственно нагруженного тела запишем шесть условий равновесия:

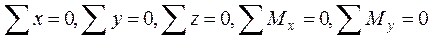и

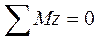
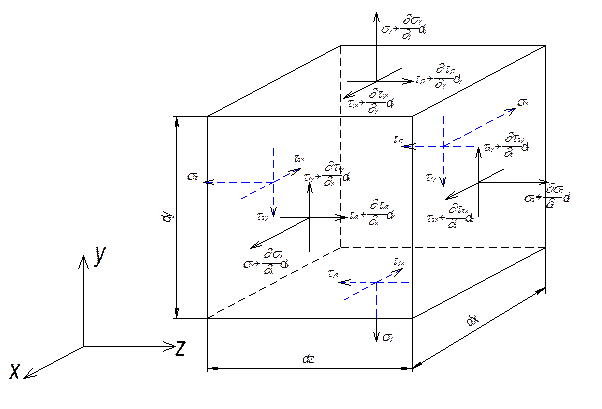Рис.7

Реализуем первое условие равновесия элемента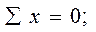

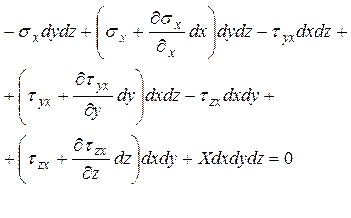
После преобразования получим

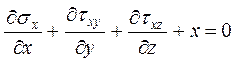(5.1)

Аналогично составим уравнение из услови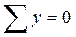й и .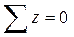

Таким образом получаем систему дифференциальных уравнений в частных производных для девяти компонентов тензора напряжений

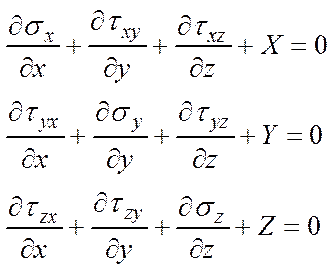(5.2)

Полученные уравнения равновесия (5.2) называется уравнением Навье.

При составлении моментных уравнений равновесия 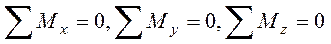Целесообразно начало координат поместится в центре элементарного параллелепипеда. Тогда из уравнений выпадут объемные и нормальные силы. Условие 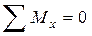дает такое уравнение равновесия 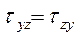. Аналогично получим

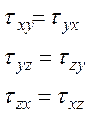
Зависимости (5.3) выражают свойство парности касательных напряжений. В силу того свойства тензор (3.4) симметричный: на его диагонали располагаются нормальные напряжения 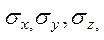а по обе стороны от неё – попарно равные касательные напряжения.

Условия равновесия граничного элемента. Статические граничные условия.

Статические граничные условия – граничные условие в напряжениях вытекают из условий равновесия элементов тела, взятых вблизи его поверхности. Особенность частиц тела на поверхности состоит в том, что элемент тела (в виде параллелепипеда или тетраэдра), взяты вблизи поверхности, имеет помимо площадок внутри тела так же площадку на поверхности (рис.9). Поэтому элементарный объем, охватывающий исследуемую частицу, находятся в равновесии под действием сил, приложенных к ней с одной стороны изнутри (возникающие напряжения 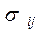), а с другой – извне тела (внешняя нагрузка). Из них последние заданы наперед, т.е. они не вытекают из законов деформирования тела.

Запишем для тетраэдра, находящегося под действием внешней нагрузки (на поверхности) Р и напряжений 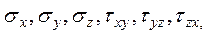действующих на внутренних гранях, условия равновесия в виде

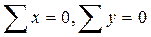и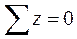

При этом обозначим через 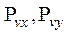и 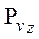- проекции вектора внешней нагрузки на координатные оси x, y, z, а

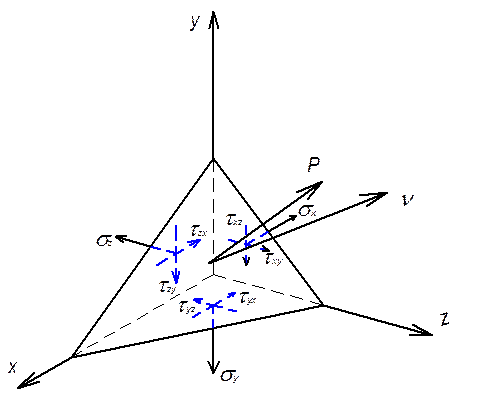
Рис.9

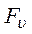- площадь наклонной (внешней) грани тетраэдра;

F_x,F_y,F_z – площади внутренних граней, перпендикулярных соответствующим координатным осям x,y,z.

Тогда

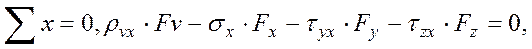
учитывая, что 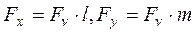и ,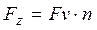

после соответствующих подстановок и преобразований получаем окончательно

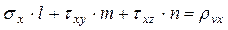
Повторив рассуждение для услови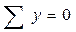й и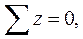

получаем условия равновесия граничного элемента, т.е. статические граничные условия

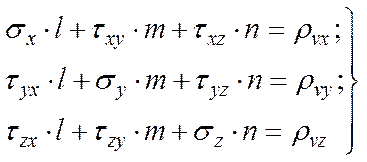(5.4)

Геометрические уравнения (Коши)

Деформации элемента обусловлены взаимным перемещениями его частиц (точек). Поэтому они в конечном счете выражаются через эти перемещения. Возьмем в теле элементарный параллелепипед, положение которого определяется координатами x, y, z вершины А (рис.10). Грани его параллельны координатным плоскостям xy, yz, zx, а ребра равны dx, dy, dz. Решаем поставленную задачу о взаимосвязи между перемещениями и деформациями для каждой грани параллелепипеда в отдельности.

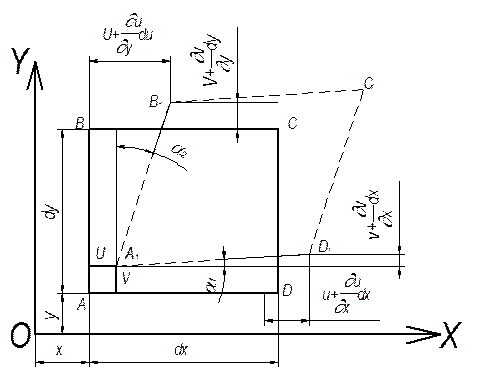
Рис.10

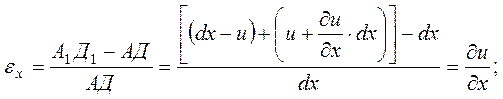
Аналогично

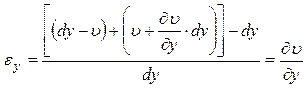
Окончательно можно записать

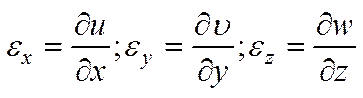(5.5)

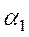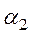
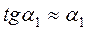Согласно определению деформации сдвига (4.4) и принимая во внимания, что при малых и и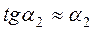

Запишем

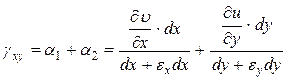
Принимая во внимание, что величины 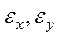ничтожно малы по сравнению с единицей, поэтому их значениями в знаменателях можно пренебречь. И далее получим

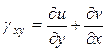
Аналогично

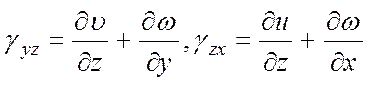(5.6)

Полученные соотношения (5.5) и (5.6) и являются геометрическими уравнениями Коши, т.е.

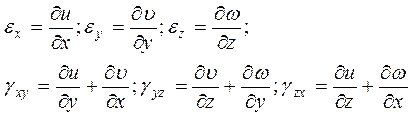(5.7)

Уравнения сплошности (неразрывности) деформаций.

Зависимости Сен-Венана

Как следует из геометрических уравнений (5.7) одному полю перемещений точек деформирующегося тела u, 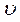, 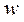соответствует единственное (конкретное) поле деформаций 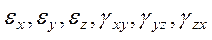, что вытекает из процедуры дифференцирования согласно зависимостям (5.7). Сложнее обстоит обратная ситуация. Одному полю деформации 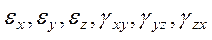могут соответствовать несколько полей перемещений u, υ, ω, что вытекает из процедур интегрирования уравнений (5.7) и, соответственно, появлению постоянных интегрирования. Единственно приемлемым – есть поле перемещений u, υ, ω, соответствующее условию сплошности (неразрывности) деформаций.

Физическую суть условия сплошности (неразрывности) деформаций можно представить в виде следующей схемы рис. (11).

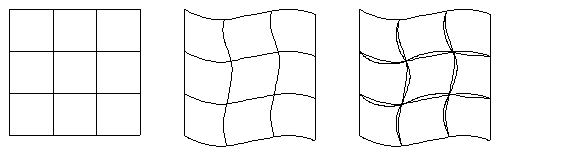а) недеформированый б) деформированый в) деформированный

элемент элемент элемент условия

условия сплошности сплошности

выполняются не выполняются.

Рис.11